Презентация на тему: Критические точки функции. Точки экстремумов

Критические точки функцииТочки экстремумов Разработка учителя математики МОУ «Курлекская СОШ» Томского района Томской области Логуновой Л.В.2006 г.

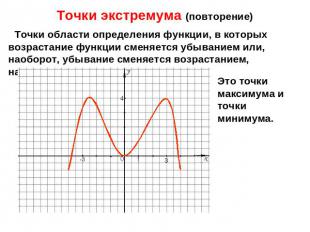
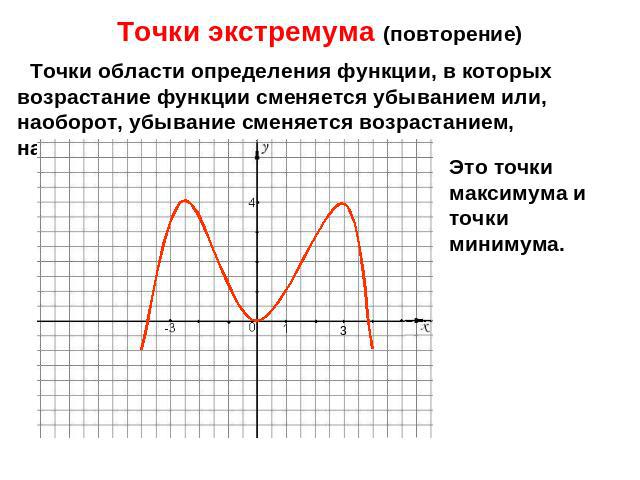
Точки экстремума (повторение) Точки области определения функции, в которых возрастание функции сменяется убыванием или, наоборот, убывание сменяется возрастанием, называются точками экстремумов.Это точки максимума и точки минимума.

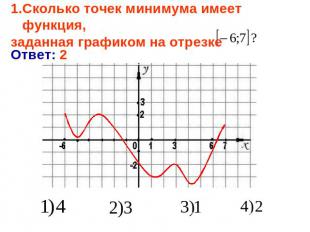
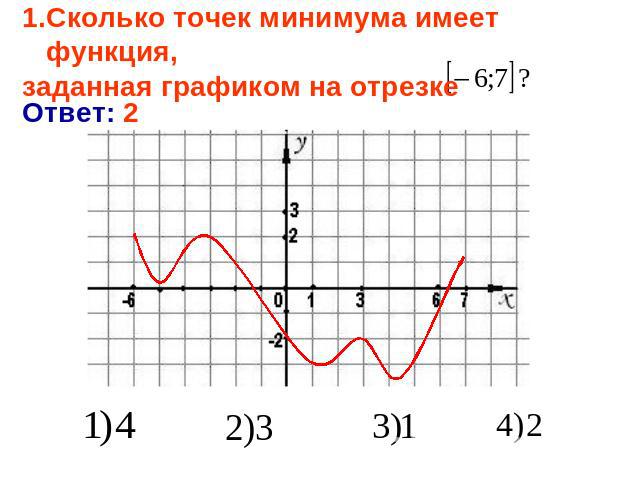
Сколько точек минимума имеет функция, заданная графиком на отрезке

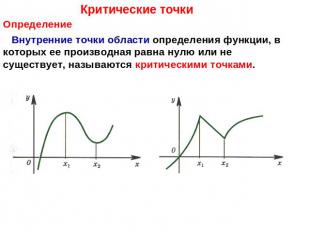
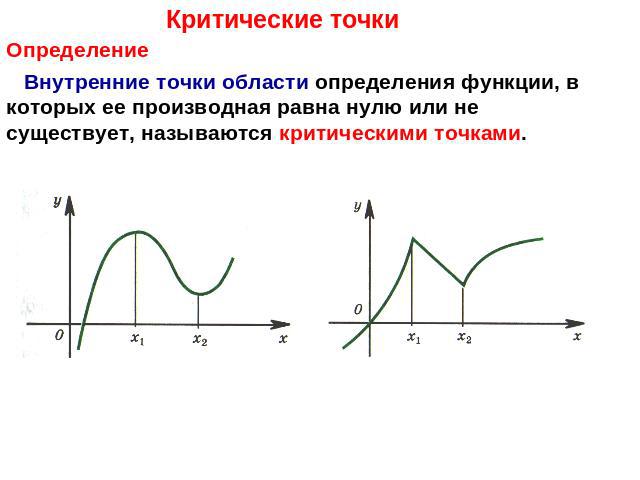
Критические точки Определение Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками.

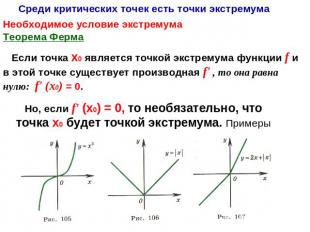
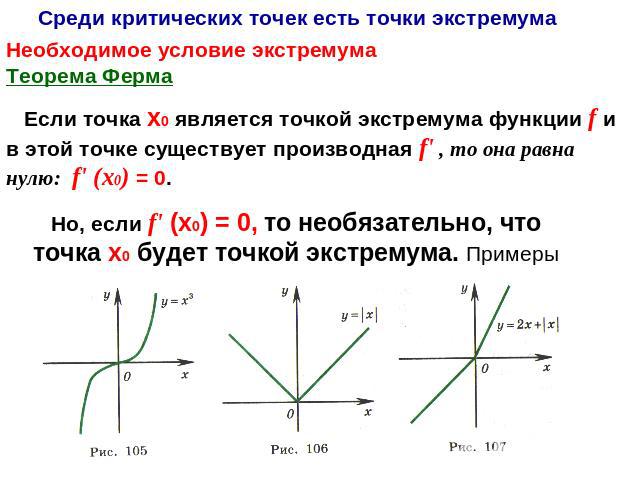
Среди критических точек есть точки экстремумаНеобходимое условие экстремумаТеорема Ферма Если точка х0 является точкой экстремума функции f и в этой точке существует производная f' , то она равна нулю: f' (х0) = 0. Но, если f' (х0) = 0, то необязательно, что точка х0 будет точкой экстремума. Примеры

Признак точки максимума функции Если функция f непрерывна в точке х0, а f' (х0) > 0 на интервале (а;х0) и f' (х0) < 0 на интервале (х0;b), то точка х0 является точкой максимума.Если при переходе через точку х0 производная от функция меняет знак с «плюса» на «минус», то точка х0 является точкой максимума.

Признак точки минимума функции Если функция f непрерывна в точке х0, а f' (х0) < 0 на интервале (а;х0) и f' (х0) > 0 на интервале (х0;b), то точка х0 является точкой минимума.Если при переходе через точку х0 производная от функции меняет знак с «минуса» на «плюс», то точка х0 является точкой минимума.