Презентация на тему: Тетраэдр. Параллелепипед

Тетраэдр и параллелепипед

Задача 1 Как при помощи шести спичек сложить четыре одинаковых треугольника?

Как называется эта фигура?

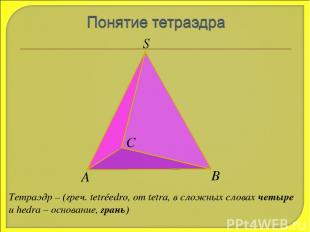
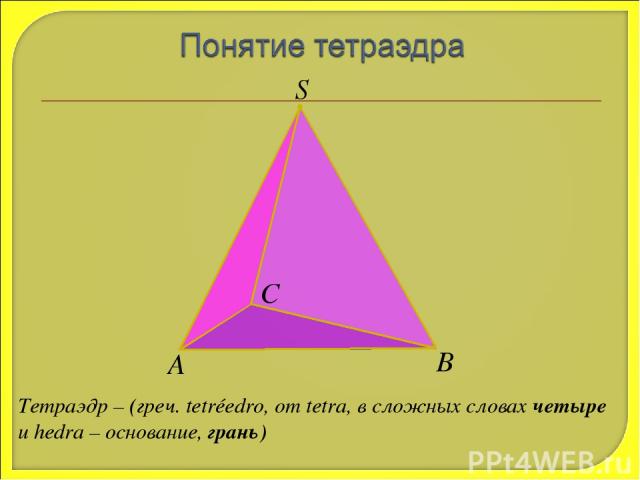
S А В С Тетраэдр – (греч. tetréedro, от tetra, в сложных словах четыре и hedra – основание, грань)

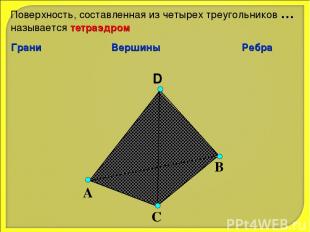
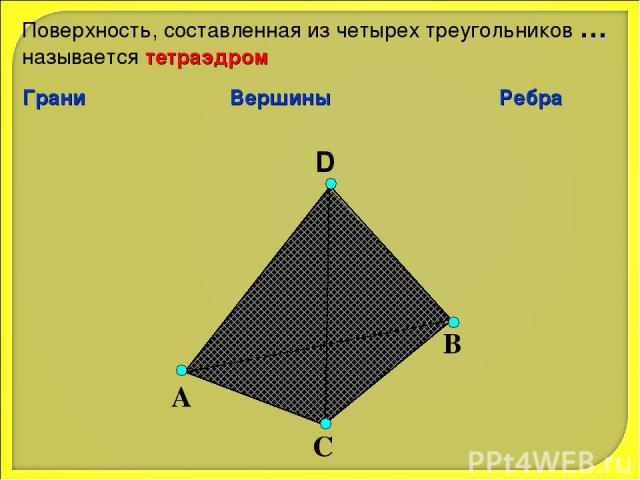
D А С В Поверхность, составленная из четырех треугольников … называется тетраэдром Грани Вершины Ребра

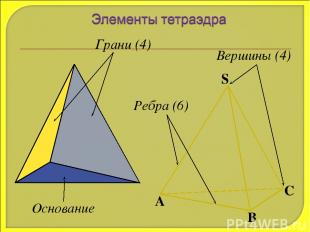
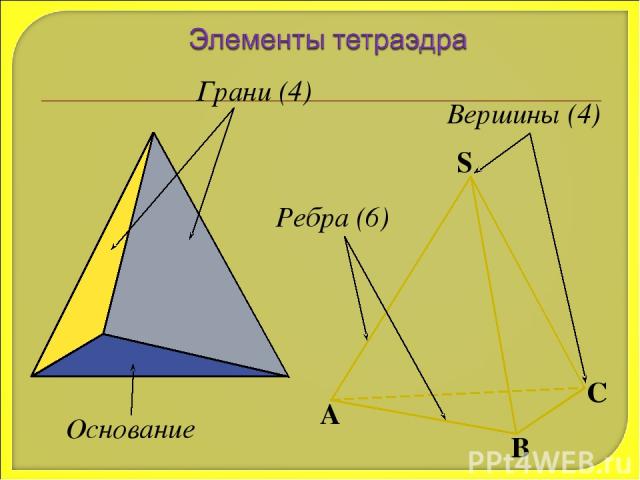
Грани (4) Ребра (6) Вершины (4) Основание

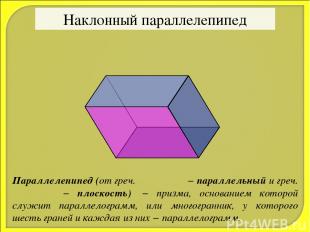
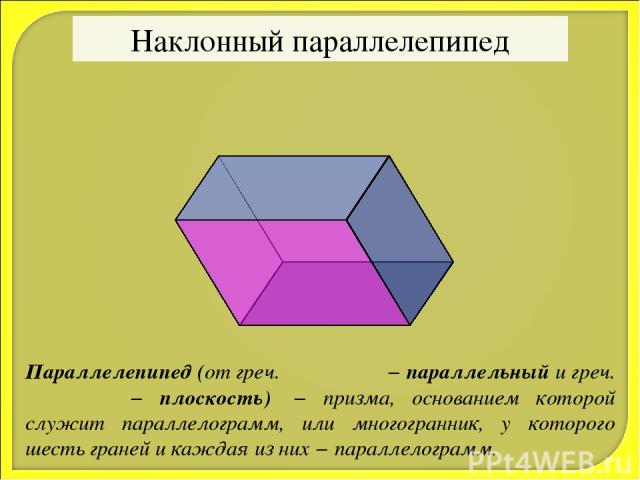
Наклонный параллелепипед Параллелепипед (от греч. παράλλος − параллельный и греч. επιπεδον  − плоскость)  − призма, основанием которой служит параллелограмм, или многогранник, у которого шесть граней и каждая из них − параллелограмм.

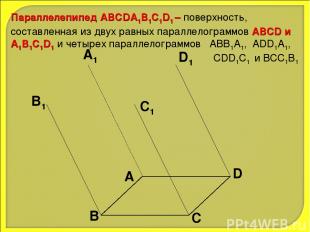
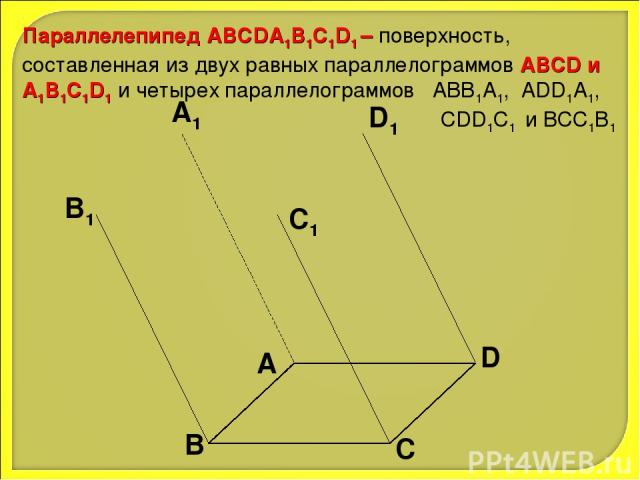
Параллелепипед АВСDA1B1C1D1 – поверхность, составленная из двух равных параллелограммов АВСD и A1B1C1D1 и четырех параллелограммов АВВ1А1, ADD1A1, CDD1C1 и ВСС1В1 А В С D

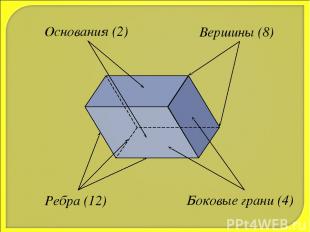
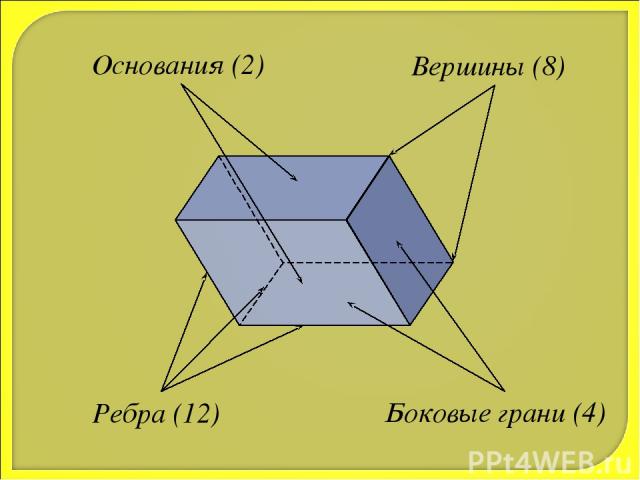
Ребра (12) Боковые грани (4) Вершины (8) Основания (2)

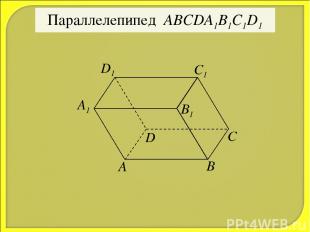
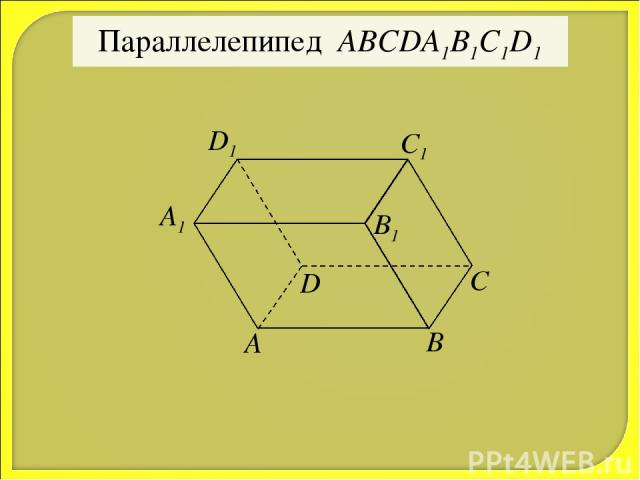
Параллелепипед ABCDA1B1C1D1

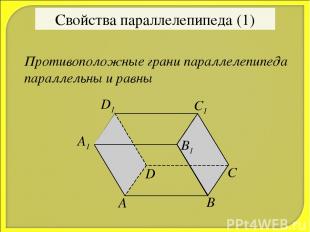
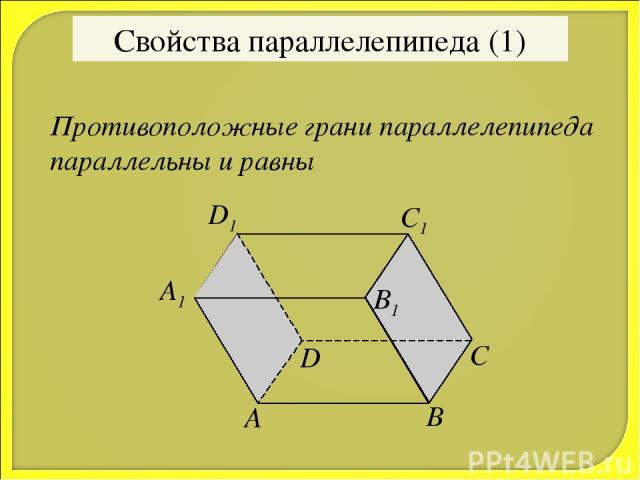
А В С А1 D D1 B1 C1 Свойства параллелепипеда (1) Противоположные грани параллелепипеда параллельны и равны

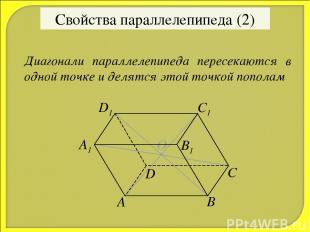
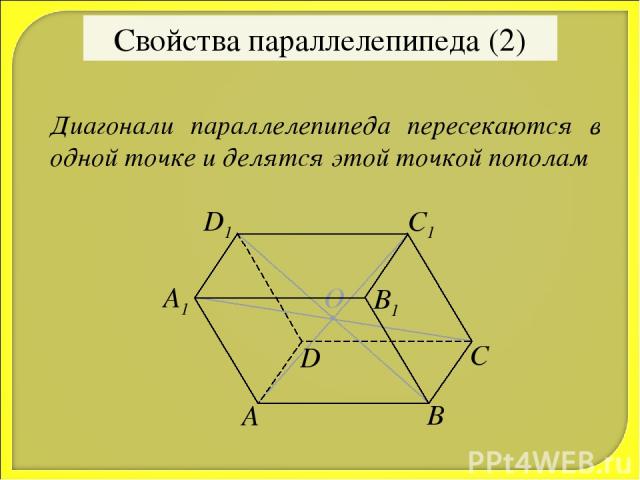
О Свойства параллелепипеда (2) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам

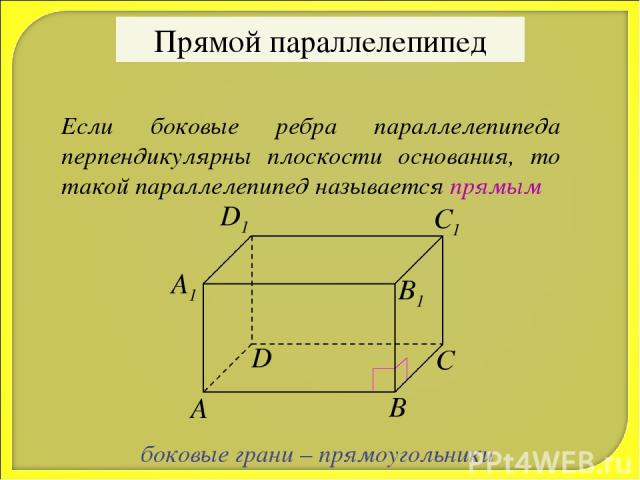
Прямой параллелепипед Если боковые ребра параллелепипеда перпендикулярны плоскости основания, то такой параллелепипед называется прямым боковые грани – прямоугольники

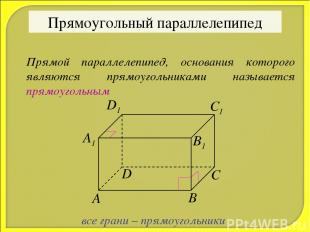
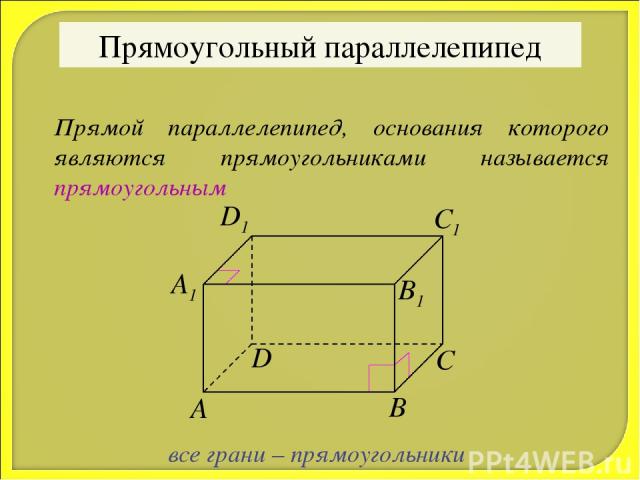
Прямоугольный параллелепипед Прямой параллелепипед, основания которого являются прямоугольниками называется прямоугольным все грани – прямоугольники

Свойства прямоугольного параллелепипеда 1° В прямоугольном параллелепипеде все шесть граней – прямоугольники 2° Все двугранные углы прямоугольного параллелепипеда– прямые

Прямоугольный параллелепипед Длины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипеда длина, ширина и высота

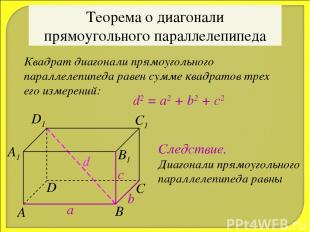
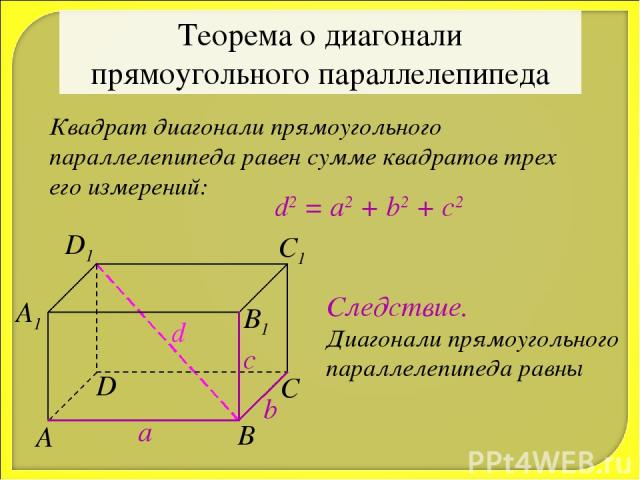
Теорема о диагонали прямоугольного параллелепипеда Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений: d2 = a2 + b2 + c2 a b c d Следствие. Диагонали прямоугольного параллелепипеда равны

Куб Прямоугольный параллелепипед, все грани которого – равные квадраты называется кубом все грани – равные квадраты d2 = 3a2 d a a a

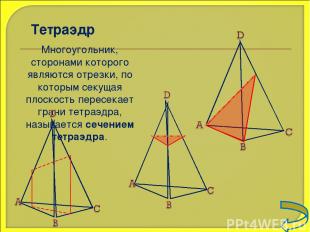
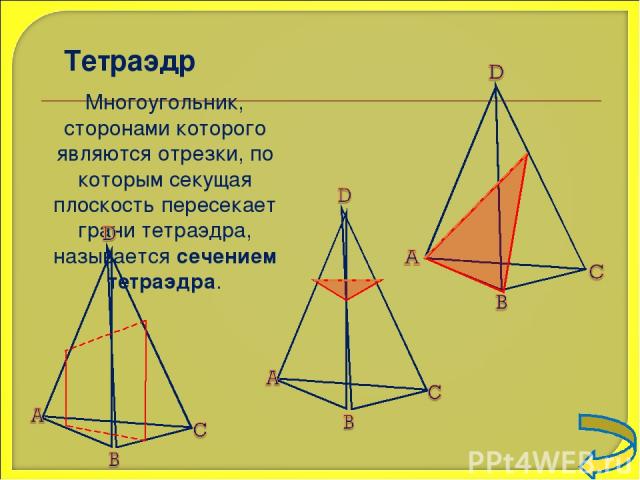
Тетраэдр Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани тетраэдра, называется сечением тетраэдра.

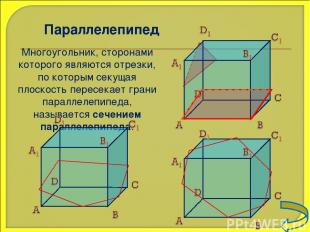
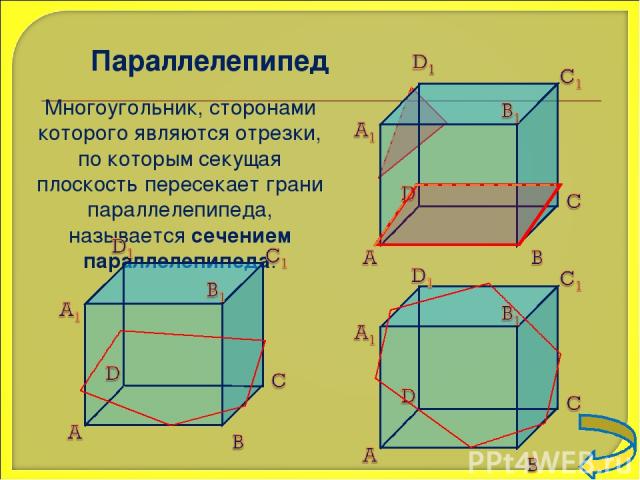
Параллелепипед Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани параллелепипеда, называется сечением параллелепипеда.