Презентация на тему: Тетраэдр и Параллелепипед

Содержание:

Многогранник составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских углов при каждой вершине равна 180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Многогранник составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских углов при каждой вершине равна 180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.

Рассмотрим произвольный треугольник АВС и точку D,не лежащую в плоскости этого треугольника. Соединим точку D отрезками с вершинами треугольника ABC,получим треугольники DAB,DBC,DCA. Поверхность составленная из четырех треугольников называется тетраэдром.

Объем тетраэдра, формула.

Определение:

Параллелепипед симметричен относительно середины его диагонали. Параллелепипед симметричен относительно середины его диагонали. Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам. Противолежащие грани параллелепипеда параллельны и равны. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. Основные формулы Прямой параллелепипед Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания Объем V=Sо*h

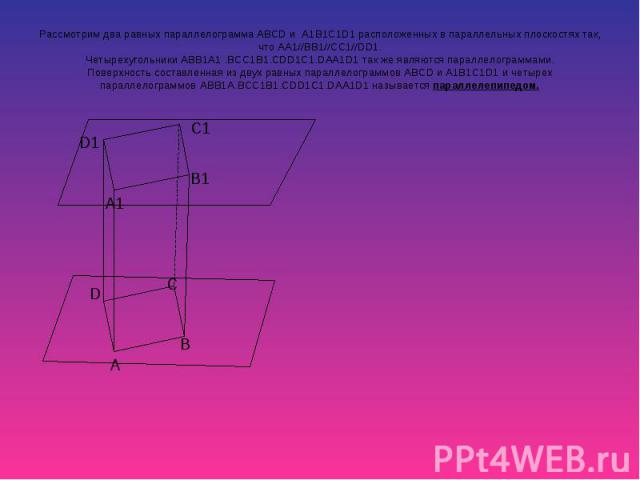
Рассмотрим два равных параллелограмма ABCD и A1B1C1D1 расположенных в параллельных плоскостях так, что AA1//BB1//CC1//DD1. Четырехугольники ABB1A1 .BCC1B1.CDD1C1.DAA1D1 так же являются параллелограммами. Поверхность составленная из двух равных параллелограммов ABСD и A1B1C1D1 и четырех параллелограммов ABB1A.BCC1B1.CDD1C1.DAA1D1 называется параллелепипедом.

Спасибо за внимание!