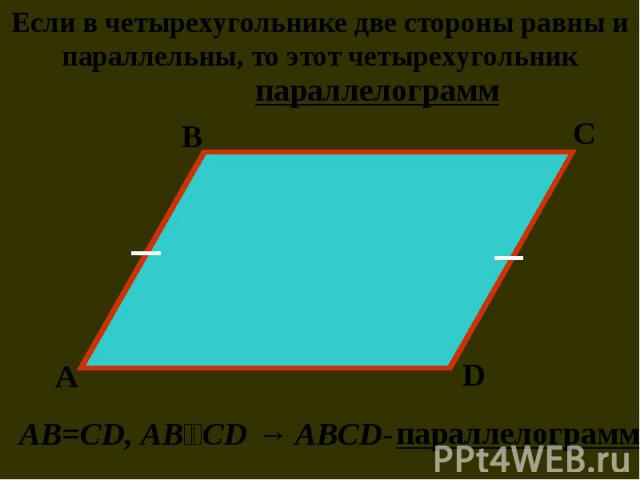
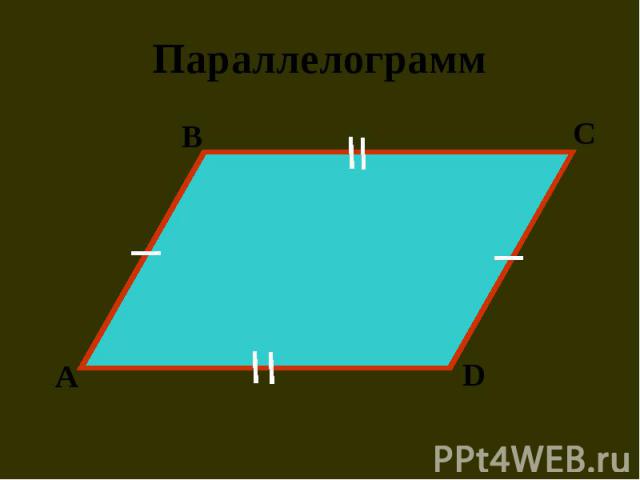
Презентация на тему: Параллельный перенос

Французский писатель 19 века Анатоль Франс однажды заметил: Французский писатель 19 века Анатоль Франс однажды заметил: «Учиться можно только весело. Чтобы переварить знания, надо поглощать их с аппетитом». Сегодня мы последуем совету писателя и будем с желанием поглощать знания, которые пригодятся нам в будущем.

План урока План урока 1. Организационный момент. 2. Задание на дом. 3. Проверка домашнего задания (опрос теории и математический диктант). 4. Актуализация опорных знаний. 5. Изучение новой темы. 6. Закрепление темы. 7. Разноуровневая практическая работа. 8. Итог урока.

п.116, п.116, вопросы 14, 15 (стр. 281) №1163(а), №1165 Принести циркуль и транспортир. По желанию сделать модель для параллельного переноса.

Отображение плоскости на себя. Отображение плоскости на себя. Выполняются следующие условия: Каждой точке плоскости ставится в соответствие какая-то одна точка этой же плоскости. Каждая точка плоскости оказывается поставленной в соответствие какой-то точке этой же плоскости.

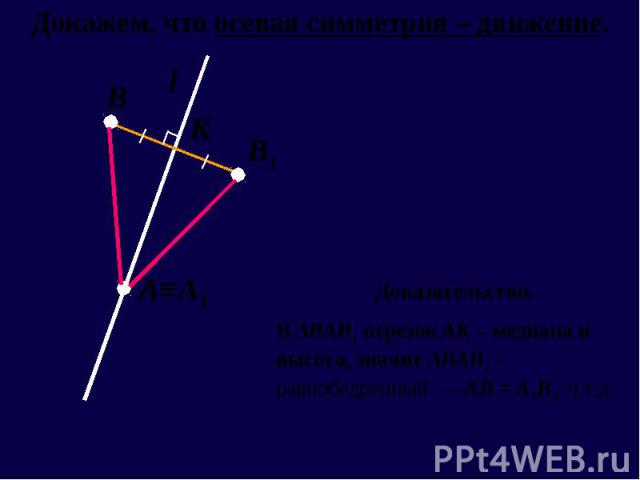
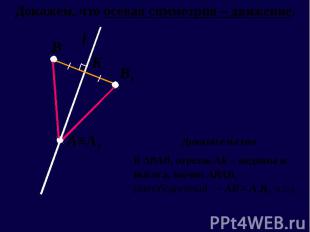
Движение – отображение плоскости на себя, сохраняющее расстояние. Движение – отображение плоскости на себя, сохраняющее расстояние. Осевая и центральная симметрия – движения. При движении: отрезок отображается на равный ему отрезок треугольник отображается на равный ему треугольник угол отображается на равный ему угол луч отображается на луч прямая отображается на прямую любая фигура отображается на равную ей фигуру

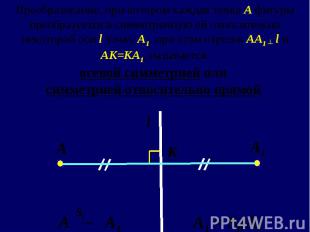
В частности, если при осевой симметрии относительно прямой l фигура Р переходит сама в себя, то она называется симметричной относительно оси l, а ось l называется ее осью симметрии. В частности, если при осевой симметрии относительно прямой l фигура Р переходит сама в себя, то она называется симметричной относительно оси l, а ось l называется ее осью симметрии.

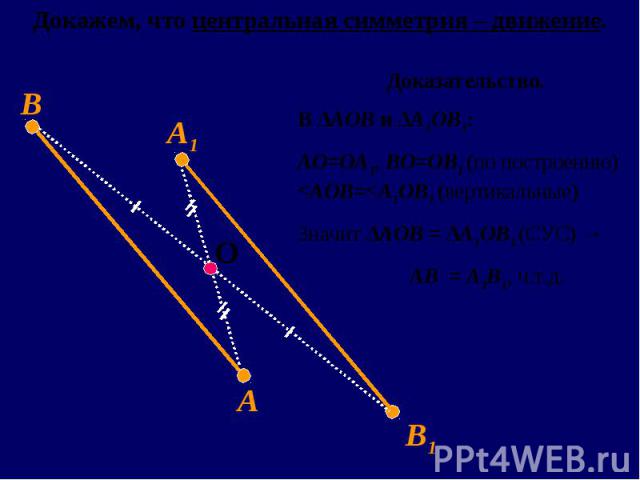
Преобразование, переводящее каждую точку А фигуры в точку А1, симметричную ей относительно центра О, называется центральной симметрией или симметрией относительно точки Преобразование, переводящее каждую точку А фигуры в точку А1, симметричную ей относительно центра О, называется центральной симметрией или симметрией относительно точки Точка О называется центром симметрии и является неподвижной. Других неподвижных точек это преобразование не имеет.

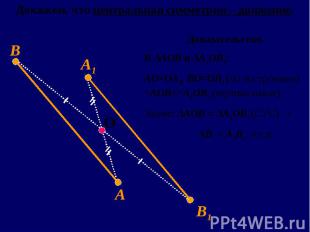
Если при центральной симметрии относительно центра О фигура Р преобразуется в себя, то она называется симметричной относительно центра О. Если при центральной симметрии относительно центра О фигура Р преобразуется в себя, то она называется симметричной относительно центра О. При этом центр О называется центром симметрии фигуры Р.

1. Отметьте точки К и М. Постройте точку К1, симметричную точке К относительно точки М. 1. Отметьте точки К и М. Постройте точку К1, симметричную точке К относительно точки М.

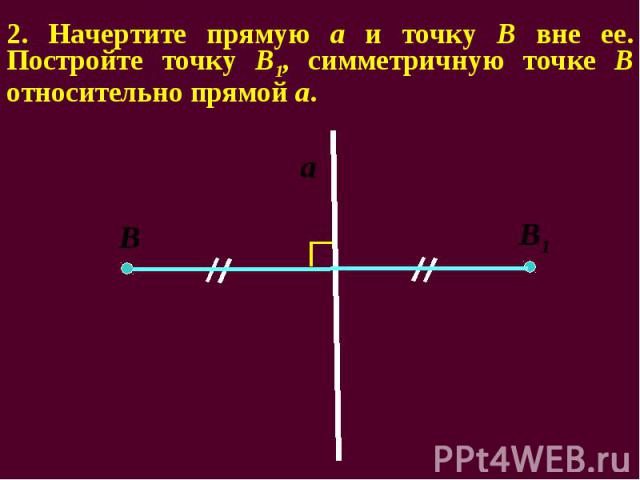
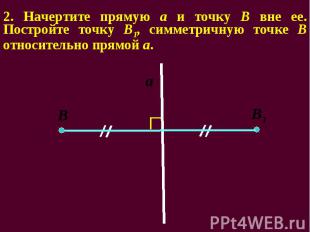
2. Начертите прямую а и точку В вне ее. Постройте точку В1, симметричную точке В относительно прямой а.

3. Закончите предложение: «Преобразование фигуры F в фигуру F1 называется движением, если оно ...». 3. Закончите предложение: «Преобразование фигуры F в фигуру F1 называется движением, если оно ...».

4. Треугольники АВС и МКР симметричны относительно некоторой точки. Стороны ΔАВС равны 6 см, 4 см и 7 см. Найти периметр Δ МКР. 4. Треугольники АВС и МКР симметричны относительно некоторой точки. Стороны ΔАВС равны 6 см, 4 см и 7 см. Найти периметр Δ МКР.

5. Два ромба симметричны друг другу относительно некоторой прямой. У первого ромба имеется прямой угол. 5. Два ромба симметричны друг другу относительно некоторой прямой. У первого ромба имеется прямой угол. Будет ли второй ромб квадратом?

6. В какую фигуру переходит при движении отрезок длиной в 9 см? 6. В какую фигуру переходит при движении отрезок длиной в 9 см?

3. Закончите предложение: «Преобразование фигуры F в фигуру F1 называется движением, если оно ...». 3. Закончите предложение: «Преобразование фигуры F в фигуру F1 называется движением, если оно ...». сохраняет расстояние

4. Треугольники АВС и МКР симметричны относительно точки. Стороны ΔАВС равны 6 см, 4 см и 7 см. Найти периметр Δ МКР. 4. Треугольники АВС и МКР симметричны относительно точки. Стороны ΔАВС равны 6 см, 4 см и 7 см. Найти периметр Δ МКР. 17 см

5. Два ромба симметричны друг другу относительно прямой. У первого ромба имеется прямой угол. Будет ли второй ромб квадратом? 5. Два ромба симметричны друг другу относительно прямой. У первого ромба имеется прямой угол. Будет ли второй ромб квадратом? Да

6. В какую фигуру переходит при движении отрезок длиной в 9 см? 6. В какую фигуру переходит при движении отрезок длиной в 9 см? В отрезок длиной в 9 см

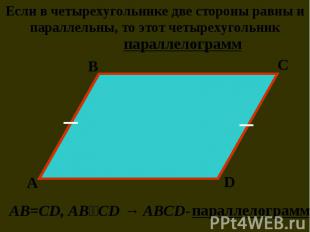
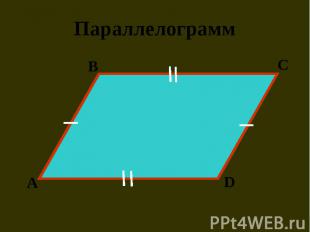
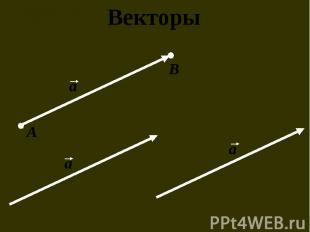
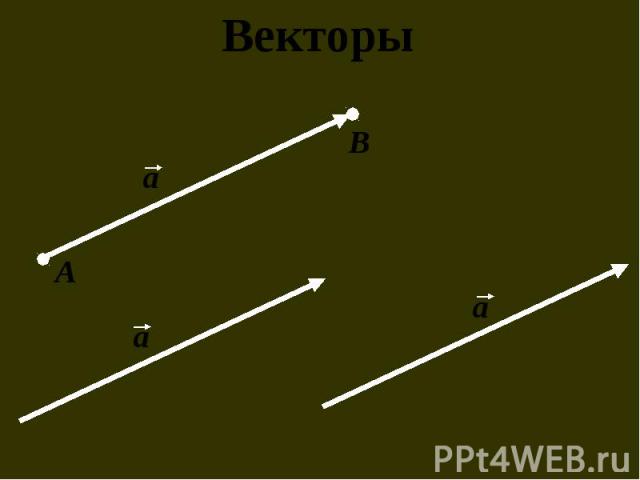
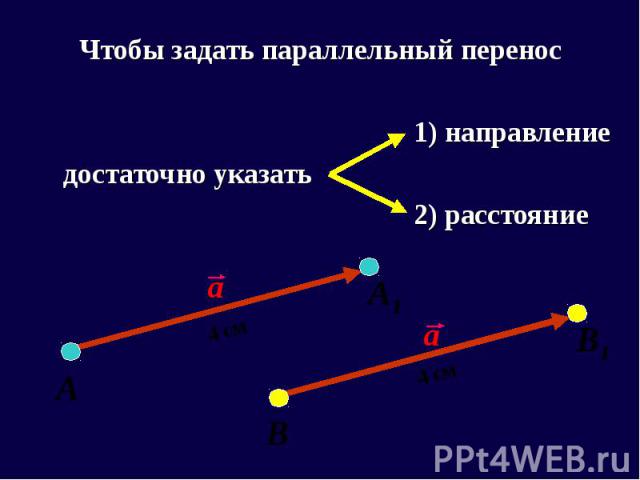
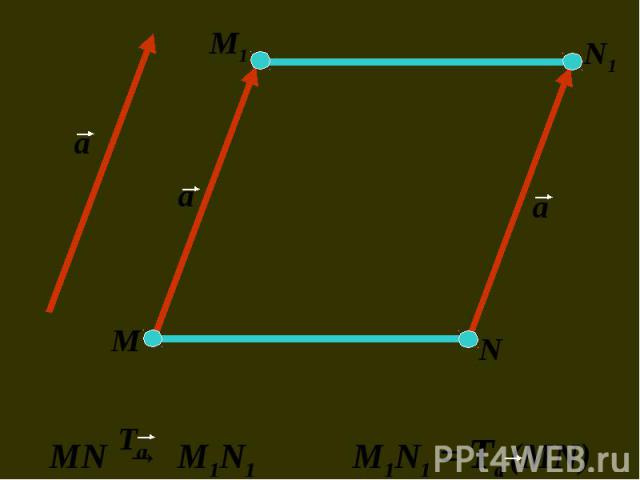
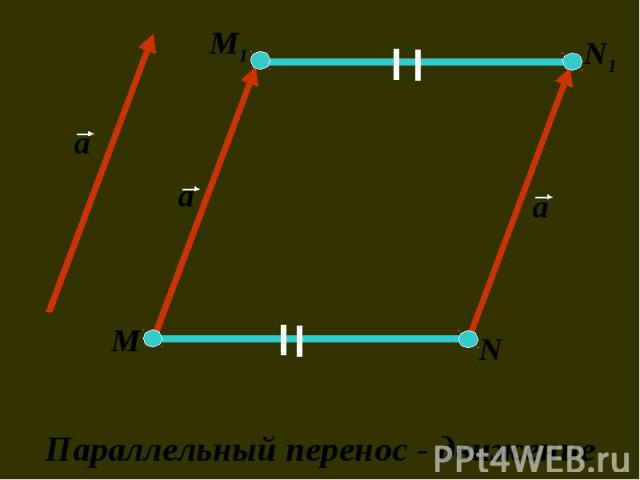
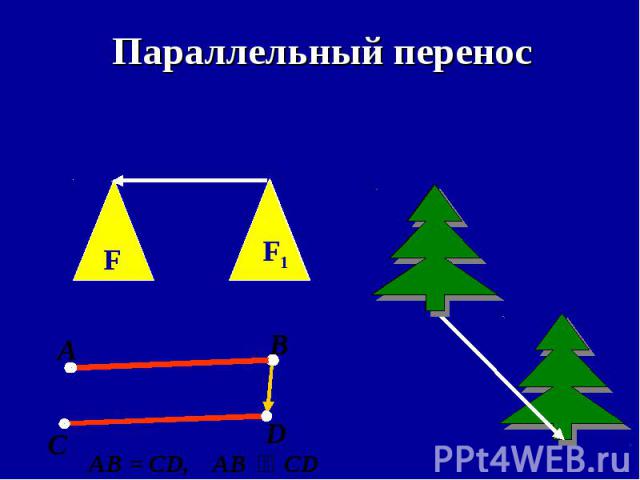
Преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении и на одно и то же расстояние называется параллельным переносом. Преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении и на одно и то же расстояние называется параллельным переносом. Чтобы задать параллельный перенос, достаточно задать некоторый вектор.

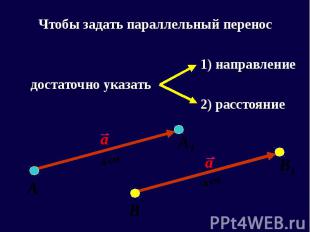
Чтобы задать параллельный перенос Чтобы задать параллельный перенос 1) направление достаточно указать 2) расстояние

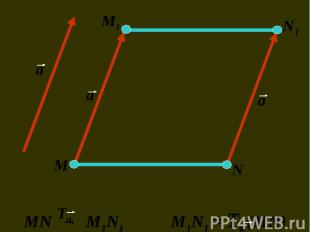
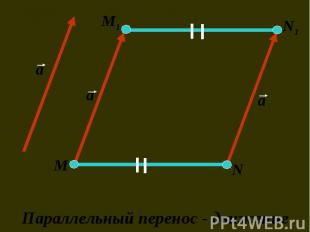
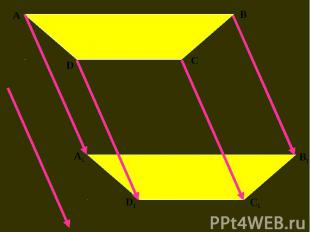
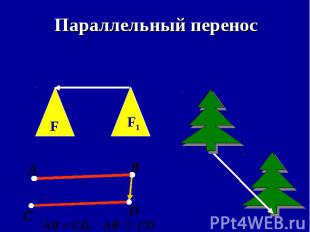
1) отрезок переходит в 1) отрезок переходит в равный ему отрезок; 2) угол переходит в равный ему угол; 3) окружность переходит в равную ей окружность; 4) любой многоугольник переходит в равный ему многоугольник; 5) параллельные прямые переходят в параллельные прямые; 6) перпендикулярные прямые переходят в перпендикулярные прямые.

№1162, №1162, №1163(а) №1164.

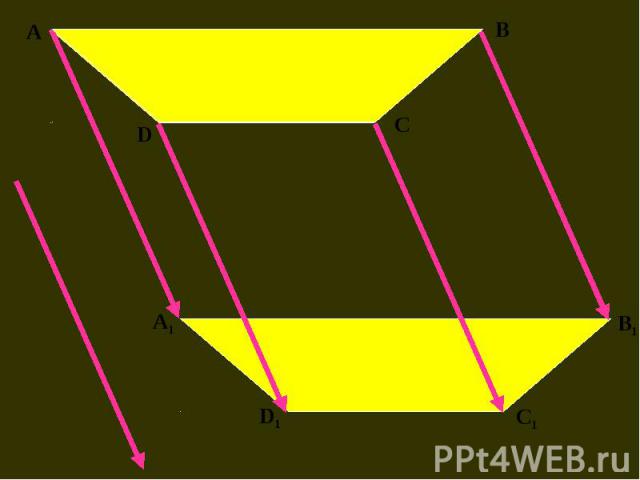
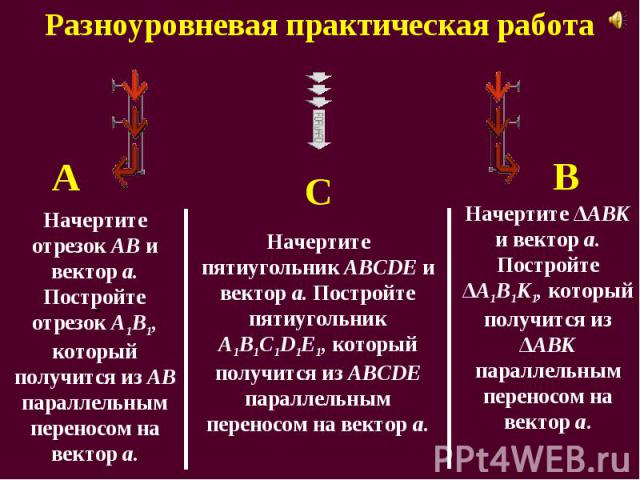
Построить образы отрезка, треугольника и четырехугольника при параллельном переносе. Построить образы отрезка, треугольника и четырехугольника при параллельном переносе.

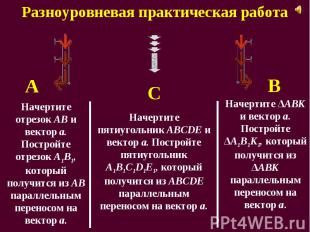
Преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении и на одно и то же расстояние называется параллельным переносом. Преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении и на одно и то же расстояние называется параллельным переносом. Чтобы задать параллельный перенос, достаточно задать некоторый вектор.