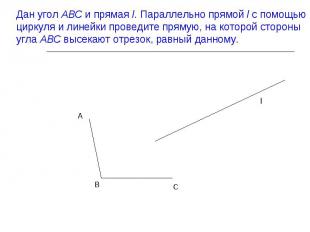
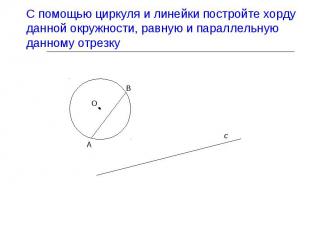
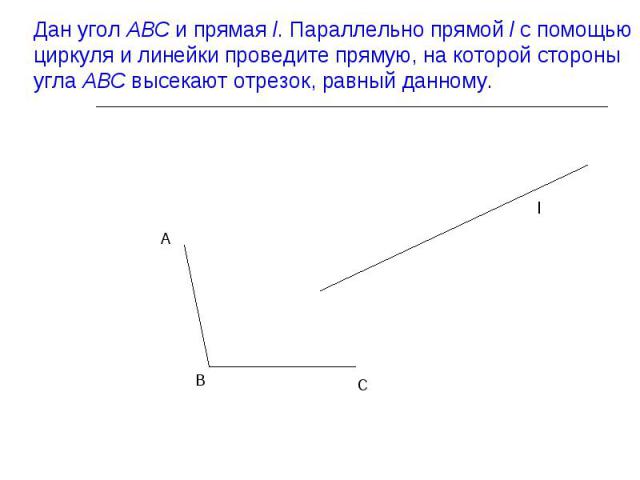
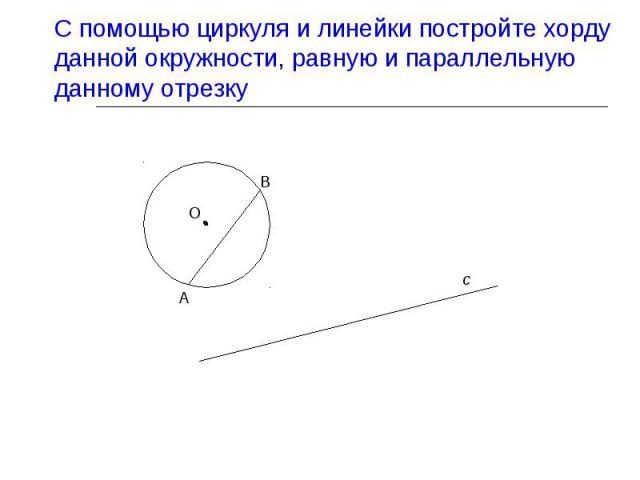
Презентация на тему: поворот и параллельный перенос

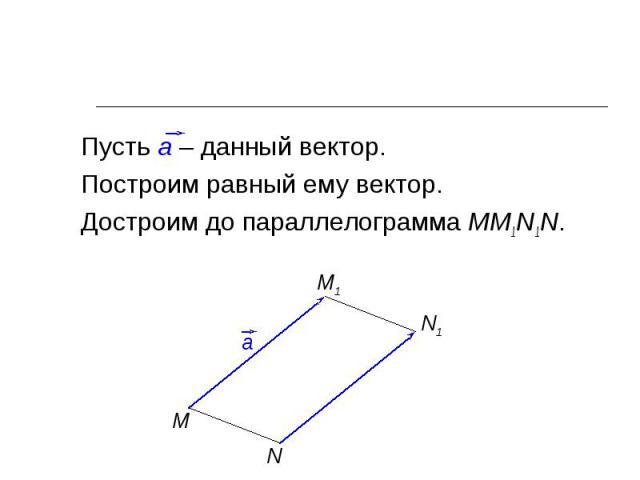
Пусть а – данный вектор. Пусть а – данный вектор. Построим равный ему вектор. Достроим до параллелограмма ММ1N1N.

Таким образом: Таким образом: Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что вектор ММ1 равен вектору а

Доказательство: Доказательство: Пусть при параллельном переносе на вектор а точки M и N отображаются в точки M1 и N1. Так как все векторы равны. Следовательно: Векторы параллельны и равны, а значит четырехугольник ММ1N1N – параллелограмм.

Значит, расстояние между векторами и точками равно. Значит, расстояние между векторами и точками равно. Таким образом, параллельный перенос сохраняет расстояние между точками и поэтому представляет собой движение.

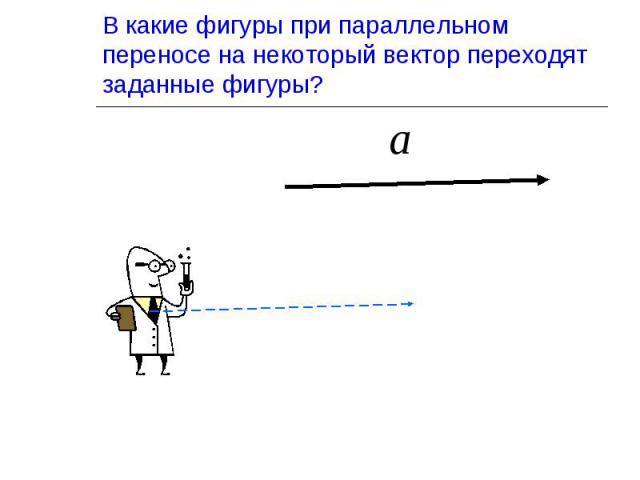
Параллельный перенос перемещает каждую точку фигуры или пространства на одно и то же расстояние в одном и том же направлении. Параллельный перенос перемещает каждую точку фигуры или пространства на одно и то же расстояние в одном и том же направлении. При параллельном переносе прямая переходит либо в себя, либо в параллельную ей прямую. Параллельный перенос задается парой соответствующих точек, т.е. каковы бы ни были точки, существует единственный параллельный перенос, при котором точка переходит в точку.