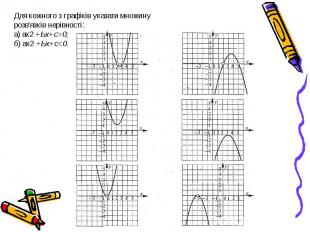
Презентация на тему: Квадратичні нерівності

з алгебри за темою

§1. Теоретичні відомості §1. Теоретичні відомості §2. Усні вправи §3. Історична довідка §4. Задачі і вправи §5. Завдання для самостійної роботи §6. Відпочинь з користю §7. Твори бо ти здібний! §8. З математикою по життю.

Квадратичною нерівністю називають нерівність, ліва частина якої є вираз___, де a ___, b, c – дані числа і x – змінна, а права - ____. Нерівності в яких знак є >, < називаються строгими та ____, якщо знак ≥, ≤. Під час розв’язання строгих, не строгих нерівностей на числовому промені точки позначають ____ та ____. Для розв’язання квадратних нерівностей використовують графік квадратичної функцій - ____. Напрям віток параболи визначається ____, якщо вітки направлені вгору, то a ____, та якщо вітки направлені ____ то а < 0. при розв’язуванні квадратних нерівностей використовуються формули знаходження дискримінанта D=____ та коренів рівняння х1=____ х2=____ або за теоремою Вієта х1 + х2 =____, х1*х2=____. Квадратичною нерівністю називають нерівність, ліва частина якої є вираз___, де a ___, b, c – дані числа і x – змінна, а права - ____. Нерівності в яких знак є >, < називаються строгими та ____, якщо знак ≥, ≤. Під час розв’язання строгих, не строгих нерівностей на числовому промені точки позначають ____ та ____. Для розв’язання квадратних нерівностей використовують графік квадратичної функцій - ____. Напрям віток параболи визначається ____, якщо вітки направлені вгору, то a ____, та якщо вітки направлені ____ то а < 0. при розв’язуванні квадратних нерівностей використовуються формули знаходження дискримінанта D=____ та коренів рівняння х1=____ х2=____ або за теоремою Вієта х1 + х2 =____, х1*х2=____.

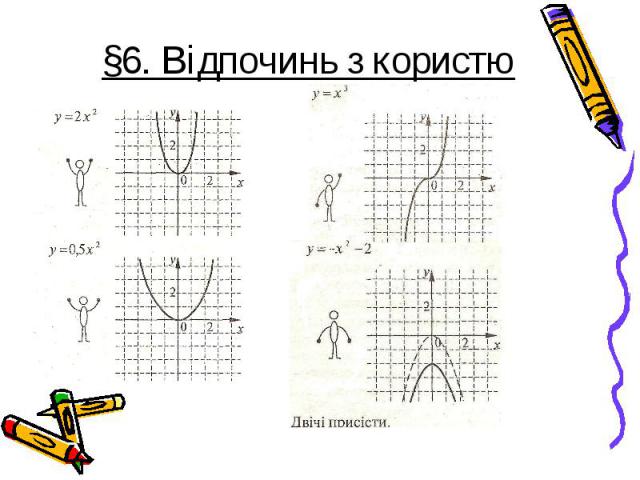
При побудові параболи для розв’язування квадратичної нерівності зручно користуватися перетворенням графіків квадратичної функції.

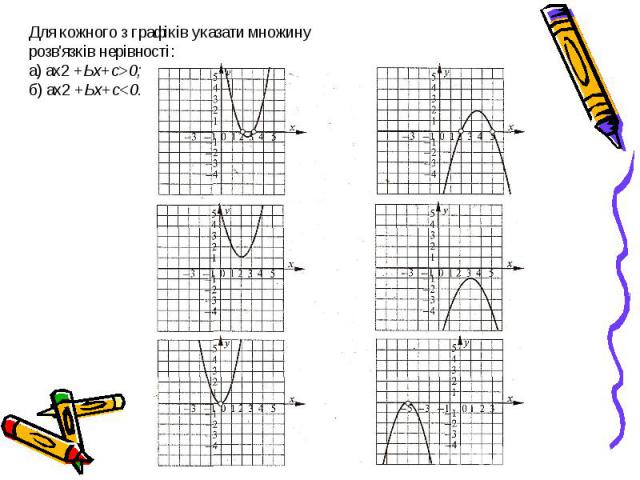
Алгоритм розв'язування квадратних нерівностей виду Алгоритм розв'язування квадратних нерівностей виду ах2 + Ьх + с>< 0. 1) Визначаємо напрямок віток параболи, яка відповідає функції у = ах2 + Ьх + с. 2) Знаходимо розв'язки квадратного тричлена ах2 + Ьх + с (розв'язуємо рівняння ах2 +Ьх + с=0). 3) Будуємо ескіз графіка функції у = ах2 + Ьх + с 4) Вибираємо значення змінної, які відповідають розв'язкам нерівності. 5) Записуємо відповідь.

Алгоритм розв'язування нерівностей методом інтервалів Алгоритм розв'язування нерівностей методом інтервалів Знайти область визначення функції у = f (х). 2) Знайти нулі функції у = f (х) (f (х) = 0) 3) Нанести нулі на область визначення. 4) Визначити знаки функції f (х) в кожному інтервалі, на які розбивається область визначення нулями функції. 5) Записати відповідь.

Розв’язати нерівність методом інтервалів (х-5)(х + 7)(х+9) <0 за поданою карткою-підказкою. Картка-підказка 1) Знайдемо нулі функції у = (х-5)(х+7)(х+9): Х1 =________; Х2 =________; Х3 =________• 2) Позначимо на координатній прямій нулі функції: х 3) Знайдемо знаки цієї функції в кожному із здобутих проміжків, скориставшись властивістю чергування знаків. 4) 3 рисунка бачимо, що множиною розв'язків нерівності є об'єднання проміжків. Відповідь.__________________________

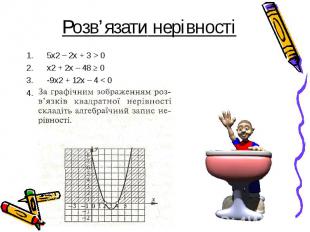
5х2 – 2х + 3 > 0 5х2 – 2х + 3 > 0 x2 + 2x – 48 ≥ 0 -9x2 + 12x – 4 < 0

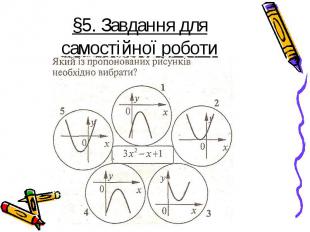
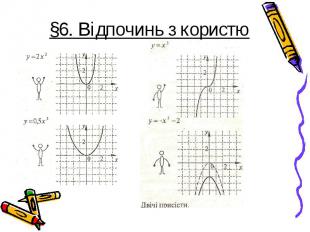
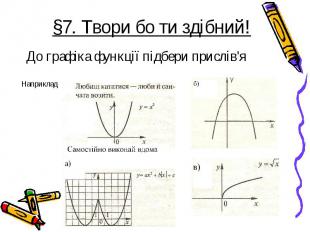
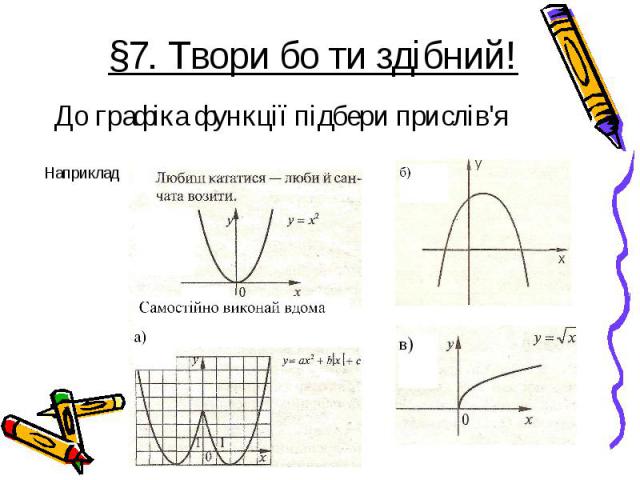
До графіка функції підбери прислів'я До графіка функції підбери прислів'я