Презентация на тему: Теория случайностей

Проект – исследование по теме «Теория случайностей» Выполнила: ученица 9 класса Бтикова Алина Руководитель: учитель математики Мулдашева А.Р.

Актуальность выбора темы моей работы объясняется тем, что в настоящее время теория вероятностей пользуется всё большей популярностью – её вводят как основной предмет в школе, в учебниках по математике ее изучают с 5 класса, на неё ссылаются в таких науках, как психология, химия, физика, биология. Объектом исследования являются азартные игры, а также их виды и связь с теорией вероятностей. Цель моего исследования – изучить основы комбинаторики, теории вероятностей, а также научиться применять полученные знания и умения в практической деятельности и повседневной жизни.

Теория вероятностей – раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Примеры:1) если бросать монету один раз, то нельзя предсказать, что выпадет герб или цифра;2) посеянное зерно может дать всход, а может и не взойти.Если это наблюдение проводить много раз, то можно заметить закономерность:1.при подбрасывании монеты отношение числа выпадений герба (цифры) к общему числу подбрасываний очень мало отличается от ½, чем больше наблюдений тем ближе к ½; 2.при посеве зерен отношение числа зерен, давших всходы, к общему числу посеянных зерен мало чем отличается от некоторого постоянного числа, с возрастанием общего числа зерен.

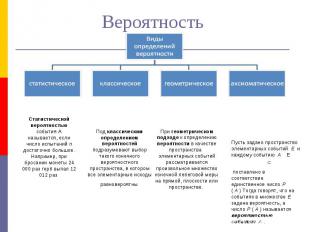
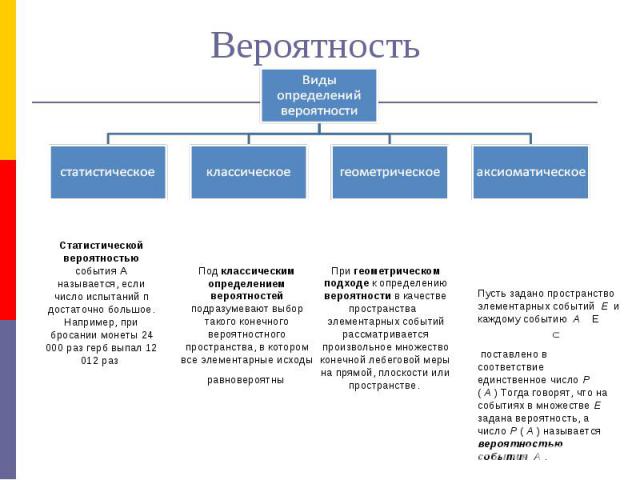
Вероятность Статистической вероятностью события А называется, если число испытаний п достаточно большое. Например, при бросании монеты 24 000 раз герб выпал 12 012 раз Под классическим определением вероятностей подразумевают выбор такого конечного вероятностного пространства, в котором все элементарные исходыравновероятны При геометрическом подходе к определению вероятности в качестве пространства элементарных событий рассматривается произвольное множество конечной лебеговой меры на прямой, плоскости или пространстве.  поставлено в соответствие единственное число Р ( А ) Тогда говорят, что на событиях в множестве Е задана вероятность, а число Р ( А ) называется вероятностью события  А .

Решение простейших комбинаторных задач Задачу имеет смысл называть комбинаторной, если ее решение состоит в переборе элементов x множества X. Как видим, такое определение описывает не саму задачу, а скорее её решение. Задача 1Сколько различных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если цифры в числе не повторяются?Решение:1) Найдем количество всех перестановок из этих цифр: P(6)=6!=720 2) 0 не может стоять впереди числа, поэтому от этого числа необходимо отнять количество перестановок, при котором 0 стоит впереди. А это P(5)=5!=120. P(6)-P(5)=720-120=600 Задача 2Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать? Решение: Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12·3=36 вариантов переплета.

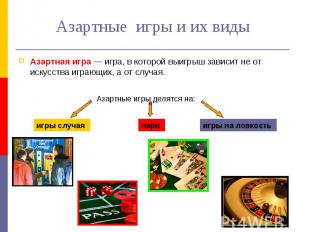
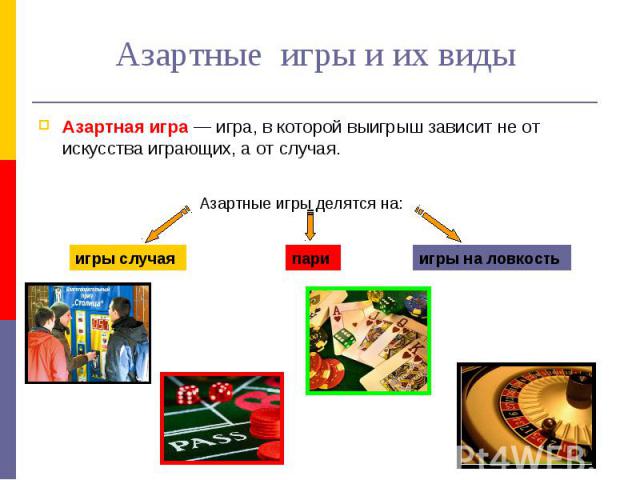
Азартные игры и их виды Азартная игра — игра, в которой выигрыш зависит не от искусства играющих, а от случая.

Исследование «случайного» Лотерея «Русское лото» данные 679 и 681 тиражей лотереи:Кол-во билетов, участвовавших в тираже;Призовой фонд игры;Стоимость билета;Кол-во выигрышных билетов;Выигрыш каждого из них;Номера и порядок выпадения бочонков. Джекпот – 3550000 руб. Кубышка – 152236 руб.В тираже участвовало 259620 билетов.Призовой фонд игры 6490500 руб.Выиграли 35897 билетов. Джекпот – 840000 руб.Кубышка – 204267 руб. В тираже участвовало 274213 билета.Призовой фонд игры 6855325 руб.Выиграли 83113 билетов Сравнение результатов. 1) 14% < 30%. Вероятность купить выигрышный билет в 681 тираже была выше, чем в 679. Это можно объяснить тем, что бочонки выпадают случайным образом, то есть количество выигрышных билетов может различаться в разных тиражах. Так, например, в 679 тираже их было примерно в 2,5 раза меньше, чем в 681 тираже. 2) 26,05р. ≈ 26,28р. Средний результат примерно одинаковый, ведь лотерея была одна и та же (с одинаковыми правилами). Однако небольшая разница обусловлена тем, что вероятность купить выигрышный билет в 681 тираже была выше, чем в 679.

Правила игры Выполнить задание игры Угадать 3 номера из 16-ти (суперигра) Дозвониться (в эфир попадает 1 человек из 400 дозвонившихся в течение 6-10 мин) Рассчитаем, какова вероятность угадать 3 числа из 16-ти. Для этого сначала посчитаем, сколькими способами можно выбрать 3 числа из 16-ти. Для этого подставим значения в формулу расчета числа сочетаний: Теперь посмотрим, сколько же человек может выиграть. Для этого перемножим вероятности:

Азартные игры и общество В анкете присутствуют такие вопросы:1. Укажите Ваш возраст, пол и род занятий.2. Как вы относитесь к азартным играм?3. Как вы думаете, насколько реально ли выиграть в какую-либо из них?4. Укажите, в какую из азартных игр, на Ваш взгляд, больше шансов выиграть?  5. Играли ли Вы когда-нибудь в азартные игры?6. Как часто Вы играете в азартные игры?7. В какие азартные игры Вы когда-либо играли?8. Насколько успешно Вы играли в азартные игры?9. Назовите свой наибольший выигрыш. 10. Назовите свой наибольший проигрыш.В опросе участвовало 25 человек. Обработанные данные были представлены в виде диаграмм:

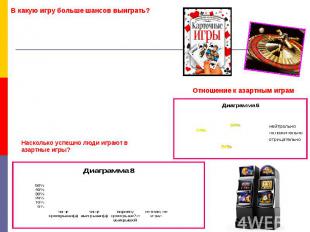
В какую игру больше шансов выиграть? Насколько успешно люди играют в азартные игры? Отношение к азартным играм

Выводы по результатам исследования общественного мнения об азартных играх. 1) Игра, в которую больше всего шансов выиграть – карточная.2) Среди опрошенных 24% никогда не играли, а 76% –играли хоть раз в жизни. Причём из тех, кто никогда не играл, 38% мужчин и 62% женщин. Можно сделать вывод, что мужчины играют чаще.3) Чаще всего отношение людей к азартным играм отрицательно, однако положительные и нейтральные отзывы тоже присутствуют.4) 12 человек из 25 опрошенных считают, что шансы выиграть в азартную игру очень малы, причём 5 из них играли в азартные игры.5) 32% опрошенных чаще проигрывали, чем выигрывали, а 8% – наоборот, у 42% примерно поровну выигрышей и проигрышей. Значит, выиграть в азартные игры сложнее, чем проиграть.

Выводы:Существует 4 вида определений вероятности: статистическое, классическое, геометрическое, аксиоматическое. Однако мной использовались лишь классическое (для решения комбинаторных задач) и статистическое (для обработки результатов опроса).Авторская задача составлена и решена с использованием правил теории вероятностей.Среди азартных игр различают игры случая, пари, игры на ловкость. В лотерею «Русское лото» и телеигру «Лови удачу» играть не выгодно, и это можно доказать путем подсчета вероятности выигрыша.Об успехе результатов проведенного мной социологического исследования говорит то, что некоторые выводы совпали с выводами ранее проведенных опросов другими людьми, результаты которых я также рассматривала.

http://efimov.mediapg.ru/webmedia_6_art_5.htmlhttp://millit.3dn.ru/publ/1-1-0-7http://mirslovarei.com/content_soc/TEORIJA-SLUCHAJNOSTI-13927.htmlhttp://www.i-loto.ru/http://ru.wikipedia.org/wiki/%D0%97%D0%BE%D0%BB%D0%BE%D1%82%D0%BE%D0%B9_%D0%BA%D0%BB%D1%8E%D1%87http://www.ruslotto.ru/