Презентация на тему: Свойства биссектрисы угла

Свойства биссектрисы угла Урок геометрии в 8 классе Учитель математики Цоколова Т.А.

Тип урока: урок усвоения новых знаний Этапы урока: - организационный - этап проверки домашнего задания - актуализация знаний учащихся - объяснение нового материала; - закрепление - проверка усвоения

Доказать, свойство биссектрисы угла (теорема) Доказать следствие Уметь применить теорему и следствие при решении задач Цели урока

Повторение (устный опрос) Определение биссектрисы угла Признаки равенства треугольников Признаки равенства прямоугольных треугольников Расстояние от точки до прямой

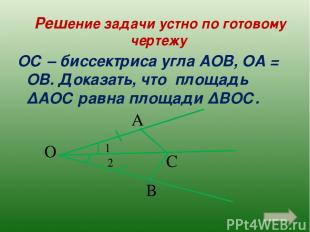
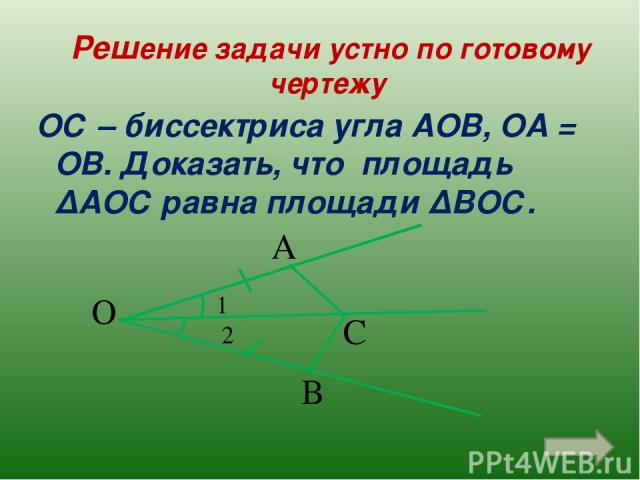
Решение задачи устно по готовому чертежу ОС – биссектриса угла АОВ, ОА = ОВ. Доказать, что площадь ∆АОС равна площади ∆ВОС. О С А В 2 1

Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Теорема

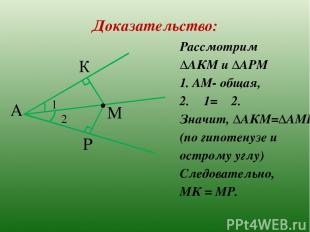
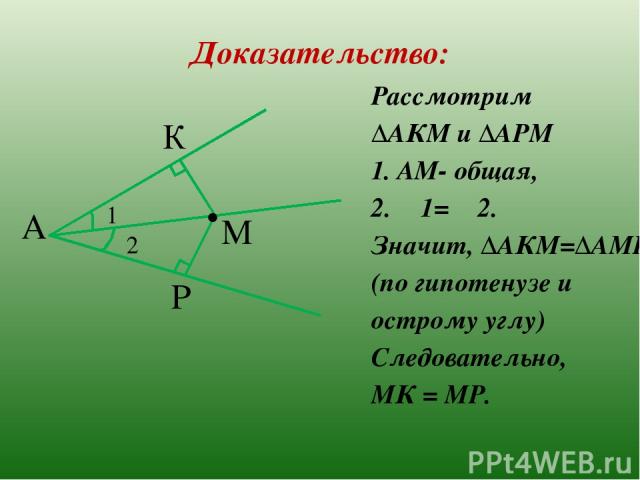
Доказательство: Рассмотрим ∆АКМ и ∆АРМ 1. АМ- общая, 2. ∟1= ∟2. Значит, ∆АКМ=∆АМР (по гипотенузе и острому углу) Следовательно, МК = МР. А К Р М . 2 1

Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе. Теорема (обратная)

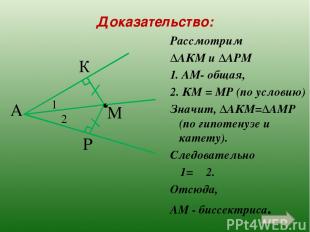
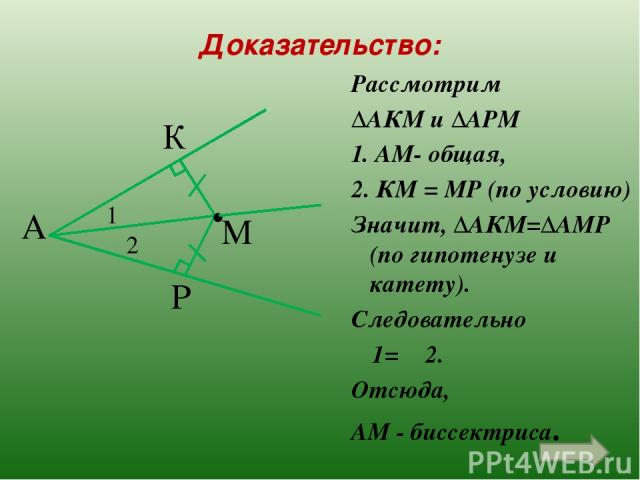
Рассмотрим ∆АКМ и ∆АРМ 1. АМ- общая, 2. КМ = МР (по условию) Значит, ∆АКМ=∆АМР (по гипотенузе и катету). Следовательно ∟1= ∟2. Отсюда, АМ - биссектриса. А К Р М . 2 1 Доказательство:

Следствие: Биссектрисы треугольника пересекаются в одной точке. A B C D E N O

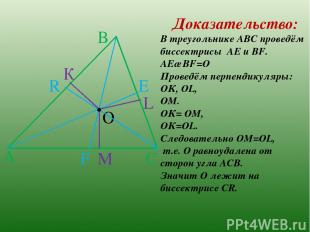
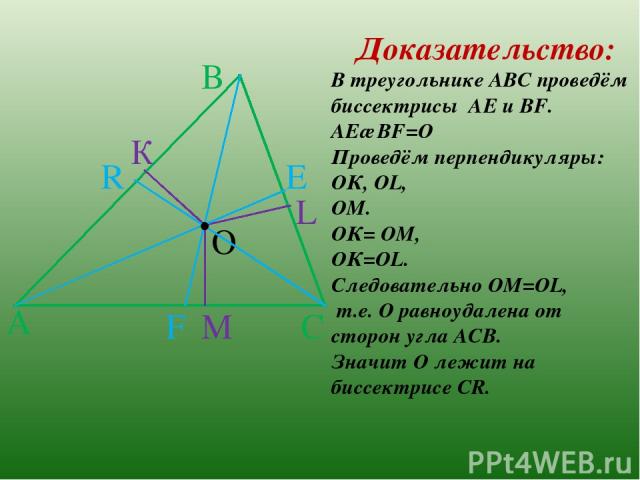
А В С . К L М О . Е F R Доказательство: В треугольнике АВС проведём биссектрисы АЕ и ВF. АЕ∩ВF=О Проведём перпендикуляры: ОК, ОL, ОМ. ОК= ОМ, ОК=ОL. Следовательно ОМ=ОL, т.е. О равноудалена от сторон угла АСВ. Значит О лежит на биссектрисе СR.

Выучить: Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе Биссектрисы треугольника пересекаются в одной точке

Закрепление (номера из учебника)

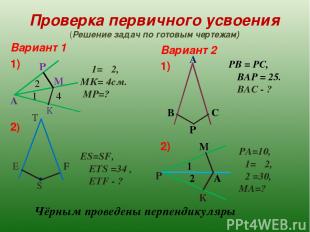
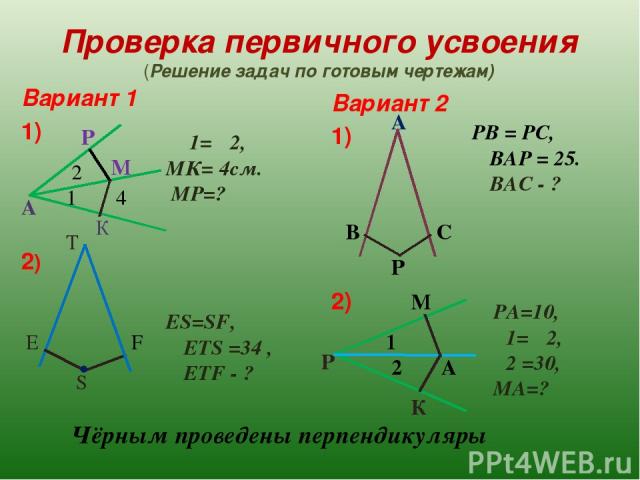
Проверка первичного усвоения (Решение задач по готовым чертежам) Вариант 1 1) 2) Вариант 2 1) 2) 1 2 4 M ∟1=∟2, МК= 4см. МР=? ES=SF, ∟ETS =34 , ∟ETF - ? P К А Т F E S . А В С Р РВ = РС, ∟ВАР = 25. ∟ВАС - ? РА=10, ∟1=∟2, ∟2 =30, МА=? М Р К А 2 1 Чёрным проведены перпендикуляры

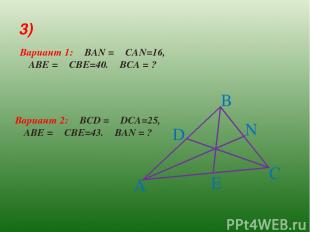
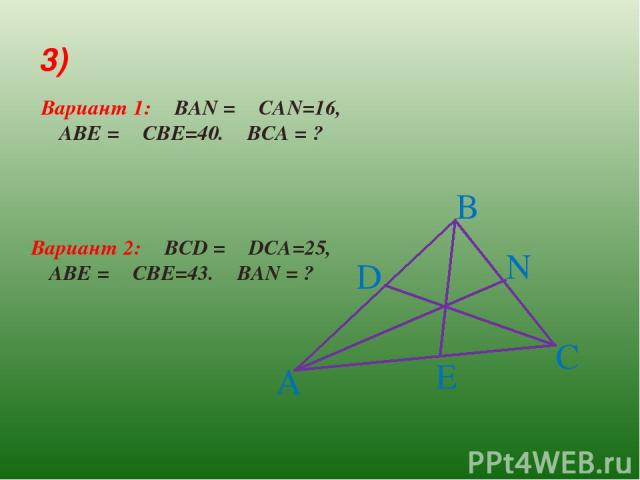
3) A B C D E N Вариант 1: ∟ВАN = ∟CAN=16, ∟AВE = ∟CBE=40. ∟ВCА = ? Вариант 2: ∟ВCD = ∟DCA=25, ∟AВE = ∟CBE=43. ∟ВАN = ?

Ответы (взаимопроверка) Вариант1. 1) 4 2) 68 3) 22 Вариант2. 1) 50 2) 5 3) 34

Домашнее задание: