Презентация на тему: Способы составления и методы решения логических задач

«СПОСОБЫ СОСТАВЛЕНИЯ И МЕТОДЫ РЕШЕНИЯ ЛОГИЧЕСКИХ ЗАДАЧ» Работу выполнила Ученица 8 класса МБОУ «Гимназия №9» Канина Дарья Учитель: Канина Галина Владимировна

Логика – это необходимый инструмент, освобождающий от лишних, ненужных запоминаний, помогающий найти в массе информации то ценное, что нужно человеку. Без логики – это слепая работа». (П. Анохин)

При составлении и решении логических задач мы используем следующий алгоритм: Определение содержания текста (выбор объектов или субъектов).Составление полной информации о происшедшем событии.Формирование задачи с помощью исключения части информации или её искажения.Произвольное формулирование задачи. В случае необходимости (недостаток информации, искажение и т.д.) вводится дополнительное логическое условие.Проверка возможности решения с помощью рассуждений. Получение единственного непротиворечивого ответа означает, что условие составлено верно. Если нет, то необходимо обратиться к дополнительному п.6.В составленном условии не хватает информации, либо имеющаяся информация противоречиво искажена. Изменяем или дополняем условие задачи, после чего необходимо обратиться к п.5.

Пример использования данного алгоритма при конструировании задачи. Субъекты: мальчики Витя, Петя, Коля.Исходная информация: у Коли больше всех грибов.Для составления задачи искажаем информацию. Делаем её логически противоречивой.Известны сообщения мальчиков:Ваня говорит, что больше всего грибов собрал Петя;Петя говорит, что больше всего грибов собрал Коля;Коля говорит, что больше всего грибов собрал Витя.

Записываем условие задачи: «Мальчики собирали в лесу грибы. Витя подсчитал, что больше всего грибов собрал Петя. Петя подсчитал, что больше грибов у Коли. Коля сообщил после своего подсчёта, что больше всех собрал грибов Витя. Кто из мальчиков больше всех собрал грибов, если известно, что только один из них опередил всех и известно, что один из мальчиков сообщил верные сведения, а двое других сказали неправду?»

Рассмотрев три варианта, нетрудно установить, что решение найти невозможно. Переходим к следующему действию алгоритма.Уточняем информацию. Во-первых, допускаем, чтолгут все мальчики, и, во-вторых, дополнительно изменяем сообщение Пети: «У Коли меньше всего грибов».Решение задачи становится очевидным.

Логические тесты подразделяются на три основные группы: словесныесимволико-графическиекомбинированные

К первой группе относятся математические анаграммы и вербальные тесты. Анаграммой называется слово, в котором поменяли местами все или несколько букв по сравнению с исходным словом. Решить анаграмму – означает определить исходное слово. Примеры. 1. Решить анаграммы и исключить лишнее слово:мапряя; чул; резоток; рипетрем.

Вербальный тест – это задание типа: вставьте пропущенное словочислитель (тело) числодробь (?) знаменатель Задание состоит из двух частей. В первой части дано решенное упражнение: из двух слов «числитель» и «число» выделено новое слово «тело». Задача решающего – найти логический признак, по которому было составлено это слово.

Примеры. Найти закономерность и исключить лишний элемент а) {15; 60; 35; 12; 40; 120} б) {задача; переменная; уравнение; функция}Реши анаграммы: асонс; лосок; ракаск; редас; сенав.Восстанови цепочку слов: конец первого слова служит началом второго: логи (…) талог; чере (…) олад; высо (…) ра; брут (…) чка

Примеры Вставьте пропущенное слово математика 3≤x≤6 тема дециметр 5≤x≤8 ?Запиши недостающее слово: сантиметр – миллиметр; гектар - ? В одном классе 27 учеников. Можно ли утверждать, что в этом классе найдутся хотя бы два ученика, фамилии которых начинаются с одной и той же буквы?

Основные методы решения задач Метод рассуждений. В методике рассуждений при решении помогают: схемы, чертежи, краткие записи, умение выбирать информацию, умение пользоваться правилом перебора.Примеры. Лена, Оля, Таня участвовали в беге на 100 м. Лена прибежала на 2 с раньше Оли, Оля прибежала на 1 с позже Тани. Кто прибежал раньше: Таня или Лена и на сколько секунд?

Решение. Составим схему:Лена ___________Оля _________ __ __ 1с 1сТаня __________ __ 1с Ответ. Раньше на 1с пришла Лена.

Любое натуральное число от 1 до 10 можно записать:а) четырьмя тройками;б) четырьмя четвёрками;использую при этом любые математические знаки. Ответ: а) 33 : 33 = 1 б) 44 : 44 = 1 3 : 3 + 3 : 3 = 2 4 : 4 + 4 : 4 = 2 3 · 3 – 3 – 3 = 3 (4 + 4 + 4) : 4 = 3 (3 : 3) + 3 = 4 (4 – 4) · 4 + 4 = 4 3 + 3 – 3 : 3 = 5 (4 : 4) + 4 = 5 3 + 3 + 3 – 3 = 6 (4 + 4) : 4 + 4 = 6 3 + 3 + 3 : 3 = 7 44 : 4 – 4 = 7 3 · 3 – 3 : 3 = 8 4 · 4 – 4 – 4 = 8 3 · 3 + 3 – 3 = 9 4 : 4 + 4 + 4 = 9 3 · 3 + 3 : 3 = 10 (44 – 4) : 4 = 10

Метод описания предметов и их форм. По описанию можно представить себе предмет, место или событие, которое вам никогда не доводилось видеть, Например, мамонта, Южный полюс или извержение вулкана. По приметам (признакам) преступника составляют его предполагаемый портрет – фоторобот. По признакам (симптомам) болезни врач ставит диагноз, т.е. распознаёт болезнь. Разгадывание многих загадок, шарад, решение кроссвордов основано на узнавании объекта по описанию.

Примеры. Вот два описания одного и того же времени года.«Похолодание, осадки в виде дождя и снега. Изменение окраски листьев и листопад у растений. Отлёт птиц». (Из учебника «Природоведение»)«Роняет лес багряный свой убор, Сребрит мороз увянувшее поле, Проглянет день, как будто поневоле, И скроется за край окружных гор». (А.С.Пушкин) О каком времени идёт речь? Как об этом можно догадаться?

Нарисуй фигуру по её описанию:а) четырёхугольник с равными сторонами и равными углами;б) многоугольник, у которого три стороны.Как называется каждая из этих фигур?Запиши двузначное число, которое делится на 4 и кончается цифрой 6. Сколько таких чисел?Возможно ли такое: а) он – мой дед, но я ему не внук; б) у моей сестры есть брат, а у меня нет брата?

Метод поиска родственных задач Если задача трудна, то необходимо попытаться найти и решить более простую «родственную» задачу. Это даёт ключ к решению исходной задачи. При этом полезно:а) рассмотреть частный (более простой) случай, а затем обобщить идею решения;б) разбить задачу на подзадачи;в) обобщить задачу (например, заменить конкретное число переменной),г) свести задачу к более простой.

Примеры. В угловой клетке таблицы 5Х5 стоит плюс, а в остальных клетках стоят минусы. Разрешается в любой строке или любом столбце поменять все знаки на противоположные. Можно ли за несколько таких операций сделать все знаки плюсами?

Возьмём квадрат 2Х2 (один плюс и три минуса). Можно ли сделать все знаки плюсами? Нельзя! Воспользуемся этим результатом: выделим в квадрате 5Х5 квадратик 2Х2, содержащий один плюс. Про него уже известно, что сделать все знаки плюсами невозможно. Значит, в квадрате 5Х5 и подавно этого сделать нельзя.

Метод «причёсывания задач» (или «можно считать, что…») Можно решать задачу, как придётся, а можно предварительно преобразовать её к удобному для решения виду: переформулировать условие на более удобном языке (например, на языке чертежа), отбросить простые случаи, свести общий случай к частному. Такие преобразования сопровождаются фразами: «в силу чётности», «явно не хуже», «для определённости», «не нарушая общности», «можно считать, что…»

Каждый ученик класса ходил хотя бы в один из двух походов. В каждом походе мальчиков было не больше 2/5. докажите, что всего мальчиков в классе не больше 4/7.Шёл дождь. Летели птицы. Они сели на дерево. На какое?По чему матросы ходят в кожаных ботинках?На дерево село 40 сорок. Проходил охотник, выстрелил и убил 6 сорок. Сколько сорок осталось на дереве?

Рассуждают примерно так: «Допустим, исходное утверждение неверно. Если из этого получим противоречие, то исходное утверждение верно».Примеры. 1. Существует ли самое большое число?Решение. Допустим, что существует. Тогда прибавим к этому числу единицу и получим ещё большее число. Противоречие. Значит, сделанное предположение неверно, и такого числа не существует.Есть ли самое маленькое число?

Многие задачи легко решаются, если заметить, что некоторая величина имеет определённую чётность. Из этого следует, что ситуации, в которых данная величина имеет другую чётность, невозможны. Иногда эту величину надо «сконструировать», например, рассмотреть чётность суммы или произведения, разбить объекты на пары. Заметить чередование состояния, раскрасить объекты в два цвета и т.д.

Кузнечик прыгал вдоль прямой и вернулся в исходную точку (длина прыжка 1м). Докажите, что он сделал чётное число прыжков.Решение.Поскольку кузнечик вернулся в исходную точку. Количество прыжков вправо равно количеству прыжков влево, поэтому общее количество прыжков чётно.

Барсук позвал к себе гостей:Медведя, рысь и белку.И подарили барсукуПодсвечник и тарелку.Когда же он позвал к себеРысь, белку, мышку, волка,То он в подарок получилПодсвечник и иголку.Им были вновь приглашеныВолк, мышка и овечка.И получил в подарок онИголку и колечко. Он снова пригласил овцу,Медведя, волка, белку.И подарили барсукуКолечко и тарелку.Нам срочно нужен ваш совет.(На миг дела отбросьте).Хотим понять, какой предметКаким подарен гостем,И кто из шестерых гостейЯвился без подарка?Не можем мы сообразить,Сидим… Мудрим… Запарка…

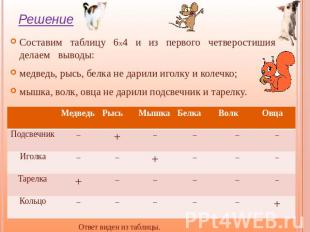
Составим таблицу 6Х4 и из первого четверостишия делаем выводы:медведь, рысь, белка не дарили иголку и колечко;мышка, волк, овца не дарили подсвечник и тарелку.Получаем таблицу:

Слово «граф» в математической литературе появилось совсем недавно. Понятие графа используется не только в математике, но и в технике и даже в повседневной жизни под разными названиями – схема, диаграмма. Особенно большую помощь графы оказывают при решении логических задач. Представляя изучаемые объекты в наглядной форме, «графы» помогают держать в памяти многочисленные факты, содержащиеся в условии задачи, устанавливать связь между ними.

В первенстве класса по теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводилось по круговой системе: каждый из участников играет с каждым из остальных один раз. Некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной и Еленой, Борис с Галиной, Виктор с Галиной, Дмитрием и Еленой. Сколько пар проведено и сколько ещё осталось?

Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах. Один из величайших математиков петербургский академик Леонард Эйлер за свою долгую жизнь (он родился в 1707 г., а умер в 1783 г.) написал более 850 научных работ. В одной из них и появились эти круги. Эйлер писал тогда, что «они очень подходят для того, чтобы облегчить наши размышления». Наряду с кругами в подобных задачах применяют прямоугольники и другие фигуры.

Часть жителей города умеет говорить только по-русски, часть – только по-узбекски и часть умеет говорить на обоих языках. По-узбекски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?Составим схему В кружке под буквой «У» обозначим жителей, говорящих по-узбекски, под буквой «Р» - по-русски. У ? Р 85% 75%

У ? Р 85% 75%В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «У» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).

Предложенный материал «Способы составления и методы решения логических задач» можно использовать как на уроках математики, так и на внеклассных занятиях учащимся 5-9-ых классов, учителями.

Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной деятельностью, собственными силами, собственным напряжением. А. Дистервег Спасибо за внимание!