Презентация на тему: Способы нахождения корней многочленов

НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА по математике: СПОСОБЫ НАХОЖДЕНИЯКОРНЕЙ МНОГОЧЛЕНОВ Исполнитель: Лукин Николай СергеевичМОУ СОШ №21, г. ПодольскНаучный руководитель: Буянова Анна Матвеевнаучитель математики МОУ СОШ №21, г. Подольск

Цели Рассмотреть решение квадратных, кубических и биквадратных уравнений; Делимость многочленов; Деление многочленов с остатком; Решение алгебраических уравнений 3-й и 4-й степени; Симметрические и возвратные уравнения; формулы Виета, Горнера и Безу. Применить полученные знания при решении задач группы С, а именно С5.

КВАДРАТНОЕ УРАВНЕНИЕ Уравнение вида ax2+bx+c=0 называется квадратным уравнением, где x – переменная, а, b и с – некоторые числа,причем, а≠0.Чтобы найти корни квадратного уравнения вида: ax2+bx+c=0, нужно найти его дискриминант. Дискриминант находится по формуле: D=b2-4ac. D>0, то уравнение имеет два корня. D=0, то уравнение имеет один корень. D<0, то уравнение не имеет корней.

ТЕОРЕМА ВИЕТА Если числа m и n таковы, что сумма равна р, а произведение равно q, то эти числа являются корнями уравнения x2+px+q=0. Частные случаи при решении квадратного уравнения

БИКВАДРАТНОЕ УРАВНЕНИЕ Уравнения вида x4+bx2+c=0 будем называть биквадратными уравнениями.Первый способ: Биквадратное уравнение можно заменой y=x2 свести к квадратному уравнению у2+by+c=0. Второй способ.

СИММЕТРИЧЕСКИЕ УРАВНЕНИЯ Уравнение видаа0хn+ а1хn-1+…+ аkхn-k+…+ аkхk+…+ а1х+a0=0 Свойствасимметрического уравнения

Пример симметрического уравнения

ВОЗВРАТНЫЕ УРАВНЕНИЯ Уравнения видаа0х2n+1+ а1x2n+…+ аnхn+1+ аn+1хn+…+ а2nх+a2n+1=0называют возвратными уравнениями нечетной степени, если где λ- некоторое действительное число.Уравнения видаа0х2n+ а1x2n-1+…+ аn-1хn+1+ аnхn+…+ а2n-1х+a2n=0называют возвратными уравнениями четной степени, если Свойства возвратного уравнения

ПРИМЕР ВОЗВРАТНОГО УРАВНЕНИЯ

ТЕОРЕМА I

ТЕОРЕМА II Пример

ТЕОРЕМА III Пример

СХЕМА ГОРНЕРА

ТЕОРЕМА БЕЗУ Пример

ФОРМУЛЫ ВИЕТА

Решение алгебраических уравнений 3-й степени с одним неизвестным

Решение алгебраических уравнений 4-й степени с одним неизвестным

Пример:

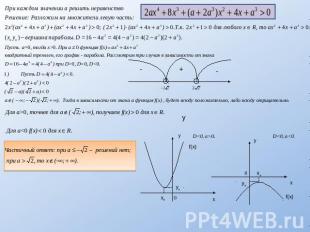
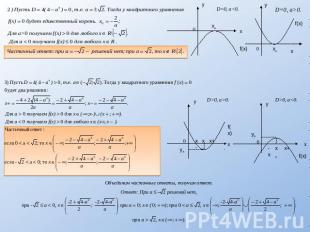
ВЫВОД: В своей работе я рассмотрел, изучил и опробовал на примере одиннадцать способов решения уравнений . Упростил запись и ход решения схемы Горнера. И я считаю, что нужно знать хотя бы самые простые способы решения уравнений высших степеней. Применил полученные знания при решении задач группы С, а именно С5.