Презентация на тему: Система двух случайных величин

Система двух случайных величин

«Теория вероятности есть ни что иное как здравый смысл , сведенный к исчислению». Лаплас

Случайной величиной называется такая величина, которая в результате опыта может принять то или иное числовое значение (из числа возможных), заранее неизвестно какое именно. Случайные величины обозначаются заглавными буквами. Случайная величина

Система случайных величин есть функция элементарного события (X,Y,…,W)=φ(ω). Каждому элементарному событию ставится в соответствие несколько действительных чисел: значения, принятые случайными величинами X,Y,…,W в результате опыта. Система случайных двух величин

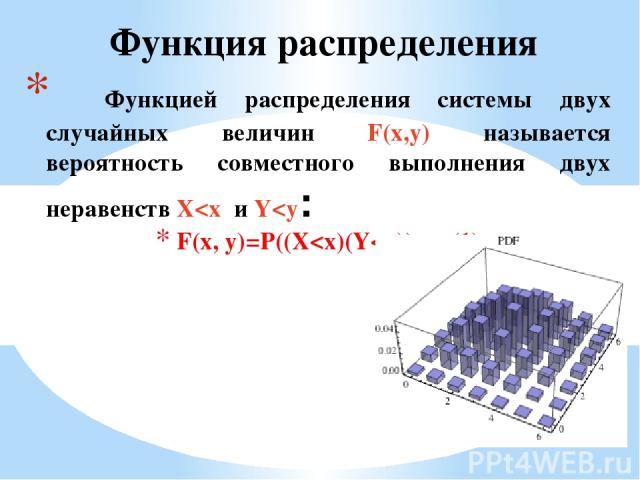
Функцией распределения системы двух случайных величин F(x,y) называется вероятность совместного выполнения двух неравенств X

Свойства функции распределения двумерной случайной величины

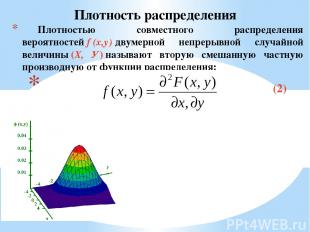
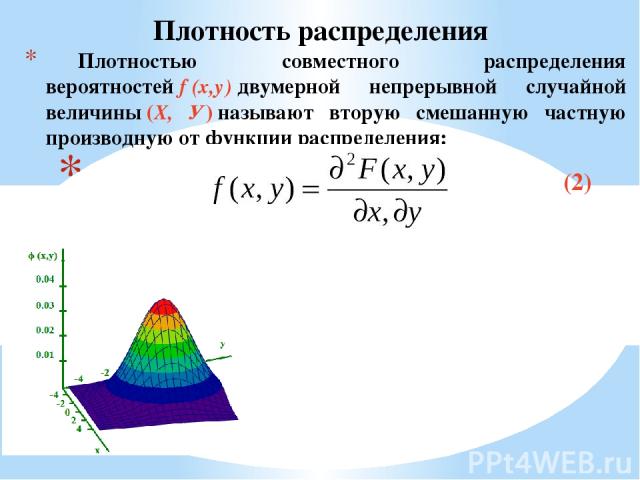
Плотностью совместного распределения вероятностей f (x,у) двумерной непрерывной случайной величины (X, У) называют вторую смешанную частную производную от функции распределения: (2) Плотность распределения

Двумерная плотность f(x, y) неотрицательна. Двойной несобственный интеграл с бес конечными пределами от двумерной плотности равен единице: (3) Свойства двумерной плотности

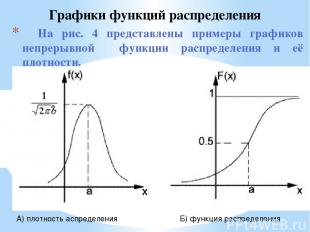
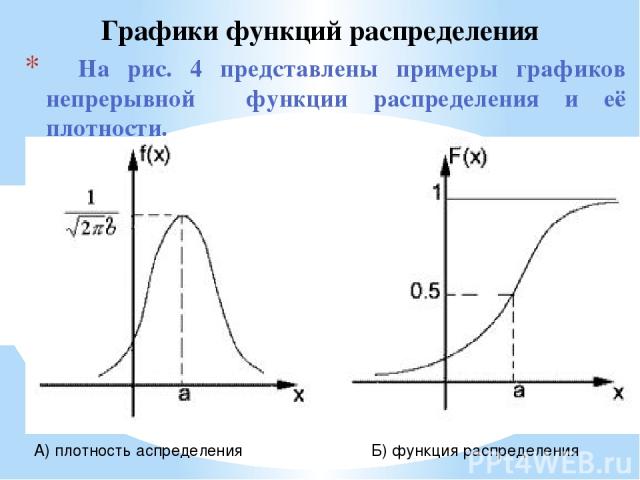
На рис. 4 представлены примеры графиков непрерывной функции распределения и её плотности. Графики функций распределения А) плотность аспределения Б) функция распределения

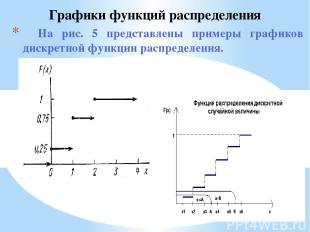
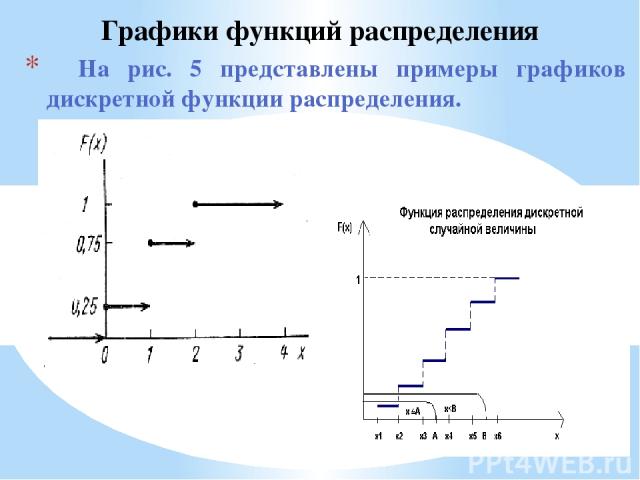
На рис. 5 представлены примеры графиков дискретной функции распределения. Графики функций распределения

Условное распределение случайной величины

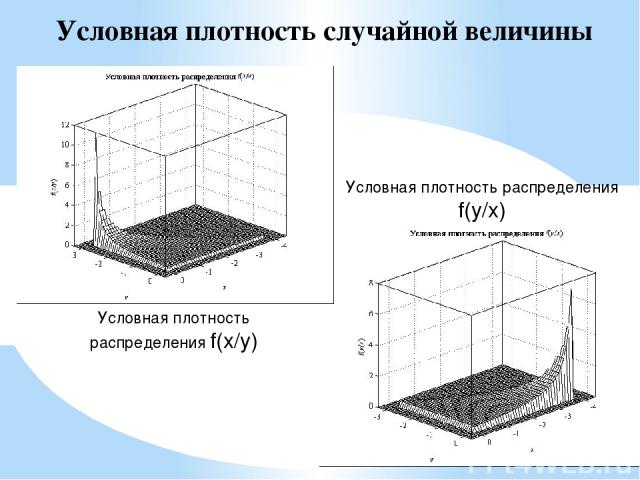
Условная плотность случайной величины

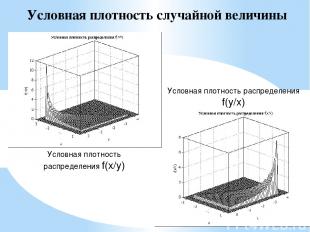
Условная плотность случайной величины Условная плотность распределения f(x/y) Условная плотность распределения f(y/x)

Спасибо за внимание