Презентация на тему: Применение производных

Применение производных Лекция 6

Содержание 1.Теоремы о дифференцируемых функциях. 2. Правило Лопиталя раскрытия неопределенностей. 3.Убывание и возрастание функции. 4. Экстремумы. 5. Выпуклость и вогнутость графика функции. Точки перегиба. 6. Асимптоты. 7. Общая схема исследования функции и построение графика.

Некоторые теоремы о дифференцируемых функциях
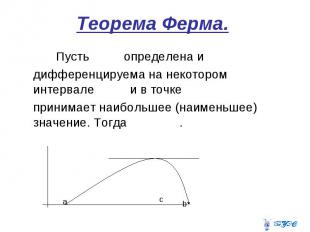
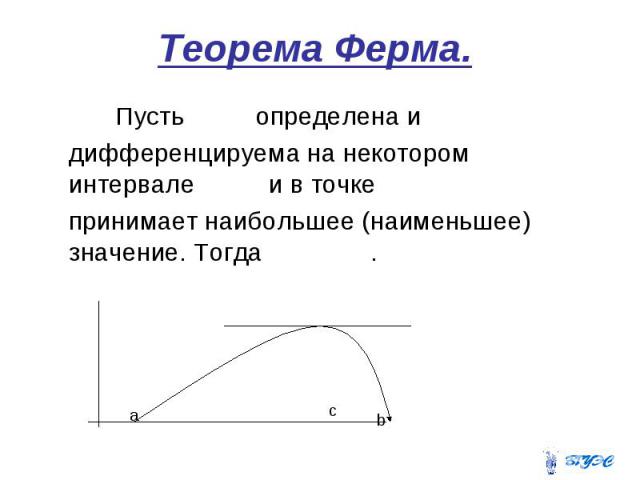
Теорема Ферма.

Теорема Ролля.

Теорема Лагранжа.
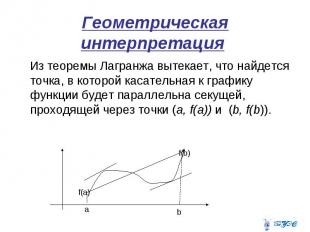
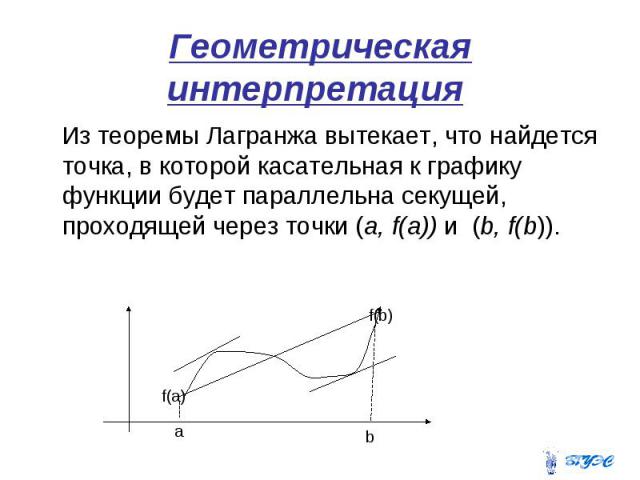
Геометрическая интерпретация Из теоремы Лагранжа вытекает, что найдется точка, в которой касательная к графику функции будет параллельна секущей, проходящей через точки (a, f(a)) и (b, f(b)).

Правило Лопиталя Пусть в некоторой окрестности О точки функции дифференцируемы всюду, кроме быть может самой точки и пусть в О.

Правило Лопиталя Если функции являются одновременно бесконечно малыми или бесконечно большими при и при этом существует предел отношения их производных, то существует и предел отношения самих функций, причем

Примеры. Правило применимо и в случае, когда 1. 2.

Примеры Найдем

Пример Найдем Прологарифмируем это выражение и найдем предел. Тогда

Убывающие и возрастающие функции

Теорема (Признак возрастания функции).

Теорема (Признак убывания функции).

Максимум и минимум функции

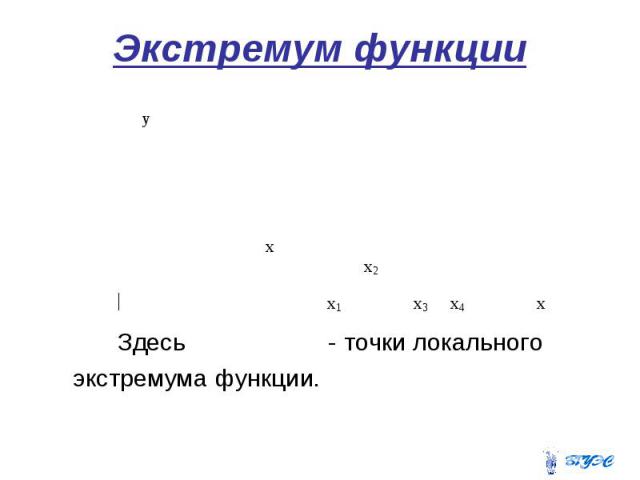
Экстремум функции
Экстремум функции

Необходимое условие экстремума Теорема. Если дифференцируемая функция имеет в точке с экстремум, то ее производная обращается в нуль в этой точке.

Экстремум функции

Продолжение Кроме точек, где , экстремумы могут быть в точках, где производная не существует или равна бесконечности

Критические точки

Критические точки

Теорема (Достаточное условие экстремума).

Найти экстремумы Приравняем производную к нулю: Проверим, меняет ли производная знаки при переходе через эти точки, для чего числовую ось разобьем точками 0 и 4/3 на интервалы (––∞, 0), (0, 4/3) и (4/3,∞ ) и найдем знаки у' в этих интервалах. В точке х = 0 имеем максимум, а в точке х = 4/3 – минимум. max y = 0,.
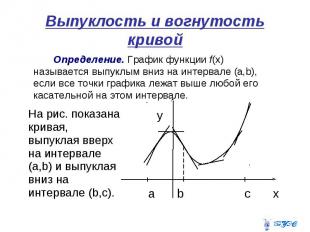
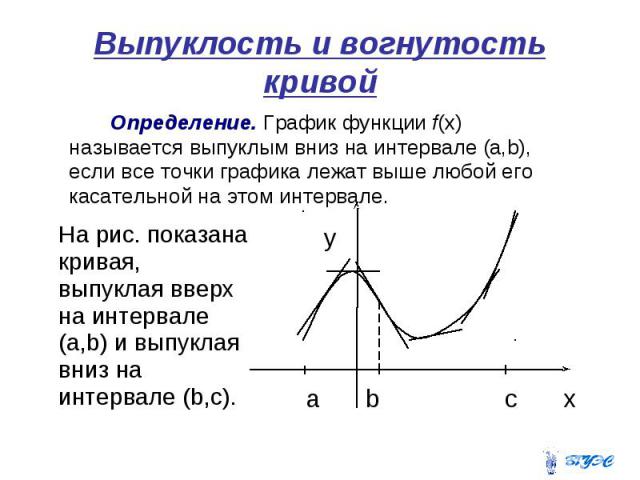
Выпуклость и вогнутость кривой

Достаточное условие выпуклости

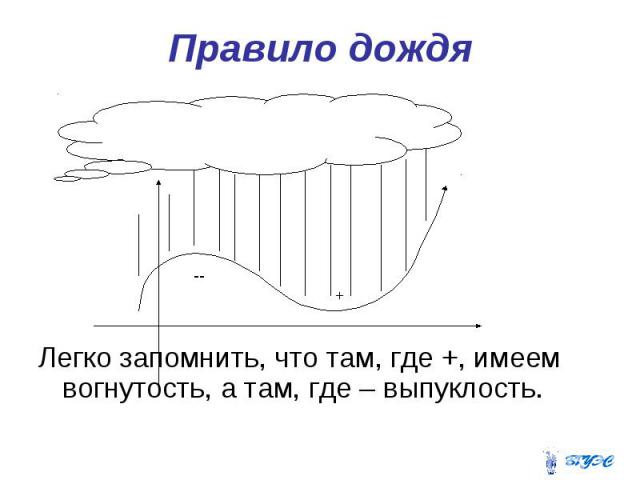
Правило дождя Легко запомнить, что там, где +, имеем вогнутость, а там, где – выпуклость.

Точка перегиба

Достаточное условие перегиба кривой
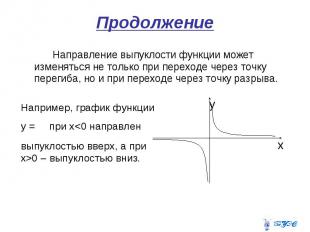
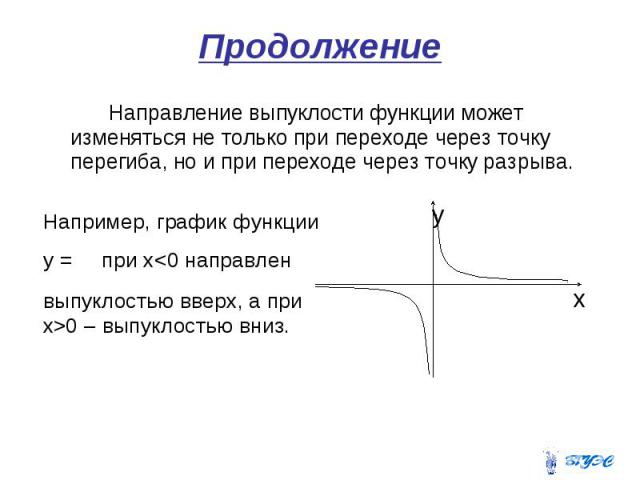
Продолжение

Асимптоты При исследовании формы кривой приходится исследовать характер изменения функции при неограниченном возрастании (по абсолютной величине) абсциссы или ординаты переменной точки кривой.

Асимптоты кривой

Пример Функция у = в точках х = 2, очевидно, имеет бесконечный разрыв, поэтому прямые х = – 2 и х = 2 являются вертикальными асимптотами кривой у = .

Наклонные асимптоты Наклонные асимптоты задают уравнением у = kх + b, где угловой коэффициент k и отрезок b, отсекаемый асимптотой на оси OY, ищут по формулам: 1) k = , b = ( f (x)– kx ) для правой асимптоты и 2) k = , b = ( f (x)– kx ) для левой асимптоты.

Общая схема исследования функции и построение графика
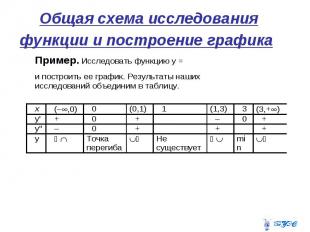
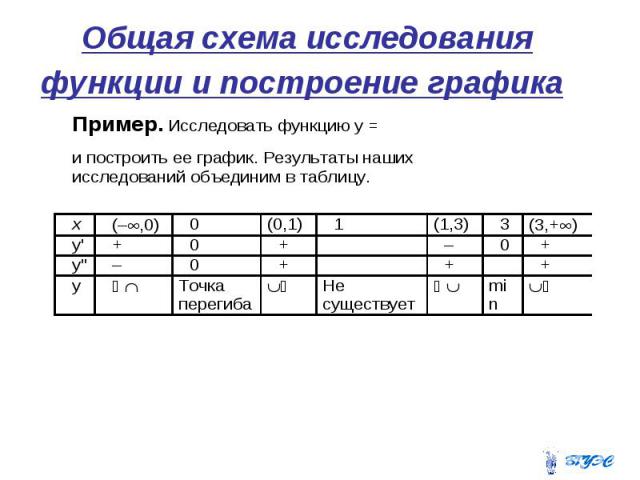
Общая схема исследования функции и построение графика
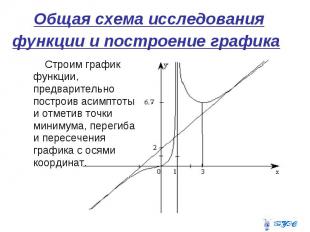
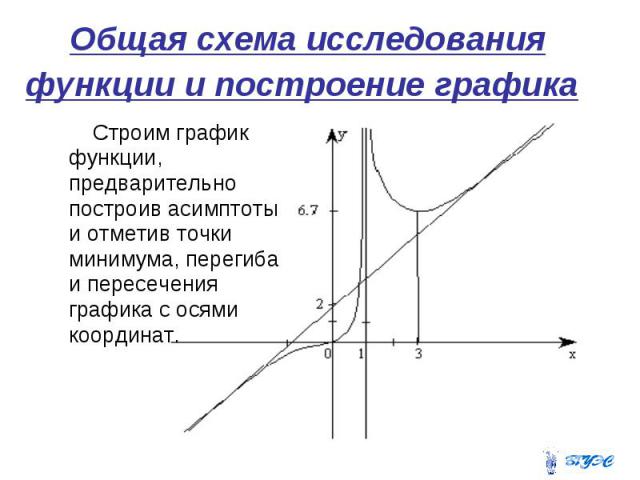
Общая схема исследования функции и построение графика