Презентация на тему: Показательные уравнения. Подготовка к ЕГЭ

Муниципальное общеобразовательное учреждение«Тарко-Салинская средняя общеобразовательная школа № 2»Обобщающий урокпо теме «Показательные уравнения» Подготовка к ЕГЭ Учитель математикиБалахнина Т. Д.

Обобщающий урокпо теме «Показательные уравнения»Подготовка к ЕГЭ Всякое умение трудом даётся Цель: Повторить и обобщить материал по теме «Показательные уравнения»;Решение показательных уравнений различных видов; Подготовка к ЕГЭ.

Задания ЕГЭ ЕГЭ - 2007В4 Найдите наибольшее значение х∙у, где (х;∙у) – решение системы: 5х (у – 0,2) = − 1, 5х – у = 5. ЕГЭ – 2008В1 Решить уравнения: а) х∙63х − 36∙63х = 0 б) 4 х +1 + 8∙4х = 3 ЕГЭ - 2009В4 Найдите х + у, где: х – у = 1, 64х – 56∙8у = 8. ЕГЭ – 2010Решите систему ур-ий:С3 5∙5 tgy + 4 = 5 -tgy, √х – 5 + 4сosy = 0.

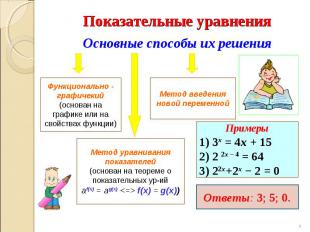
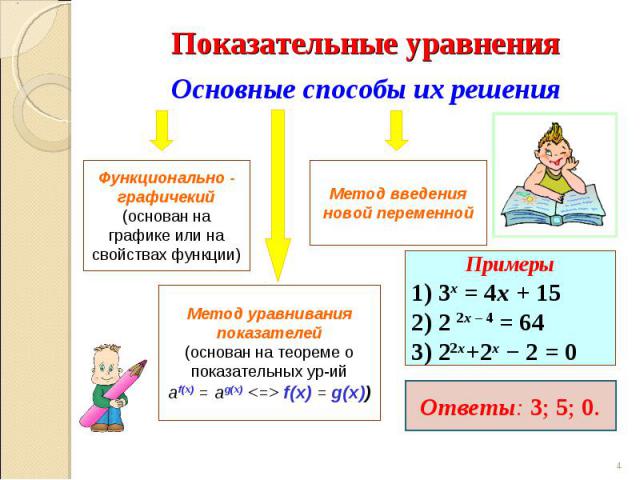
Показательные уравнения Основные способы их решения Функционально - графичекий (основан на графике или на свойствах функции) Метод введения новой переменной Метод уравнивания показателей(основан на теореме о показательных ур-ийаf(x) = ag(x) <=> f(x) = g(x)) Примеры1) 3х = 4х + 152) 2 2х – 4 = 643) 22х+2х − 2 = 0

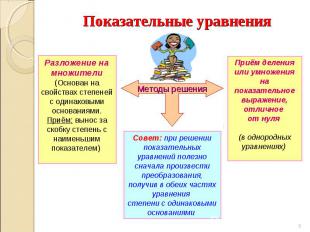
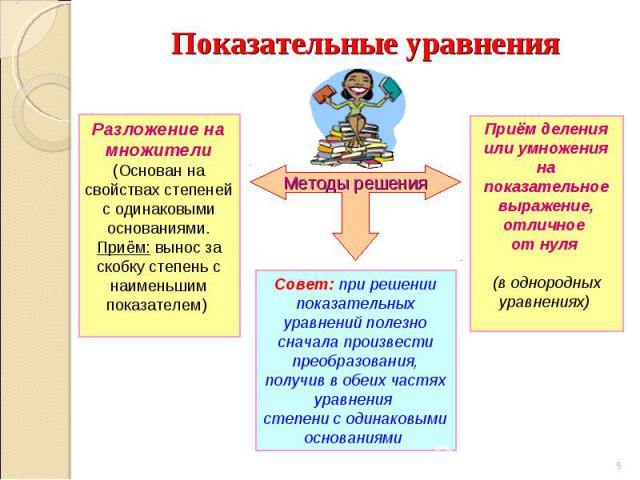
Показательные уравнения Разложение на множители (Основан на свойствах степеней с одинаковыми основаниями. Приём: вынос за скобку степень с наименьшим показателем) Совет: при решении показательных уравнений полезно сначала произвести преобразования, получив в обеих частях уравнения степени с одинаковыми основаниями Приём деления или умноженияна показательное выражение, отличное от нуля (в однородных уравнениях)

Примеры4 х + 1 − 2 ∙ 4 х – 2 = 124, 4 х – 2 ∙ (43 − 2) = 124, 4 х – 2 ∙ 62 = 124, 4 х – 2 = 2, 4 х - 2 = 40,5,… 2 ∙ 22х − 3 ∙ 2х ∙ 5х − 5 ∙ 52х = 0│ : 52х ≠ 0, 2 ∙ (2/5)2х − 3 ∙ (2/5) х − 5 = 0, t = (2/5) х (t > 0), 2t 2 − 3 t − 5 = 0, t = − 1, t = 5/2 (?...). 5/2 = (2/5)х,

В3: а) 7 х – 2 = 49, б) (1/6) 12 – 7х = 36. Ответ: а) х = 4, б) х = 2.С1: 4 х2 + 3х – 2 − 0,5 2х2 + 2х – 1= 0. (Можно 0,5 = 4– 0,5) Решение. 4 х2 + 3х – 2 = 4 −х2 − х + 0,5 х2 + 3х – 2 = −х2 − х + 0,5, … Ответ: х = −5/2, х = ½.С3: 5 ∙ 5 tgy + 4 = 5 −tgy, при сosy < 0.Указание к решению. 5 ∙ 5 tgy + 4 = 5−tgy │∙ 5 tgy ≠ 0, 5 ∙ 5 2gy + 4 ∙ 5 tgy – 1 = 0. Пусть х = 5 tgy , … 5 tgy = − 1 (?...), 5 tgy = 1/5, tgy = − 1. Так как tgy = − 1 и сosy < 0, то у … к.ч. у II к.ч., значит,

С5: При каком параметре а уравнение 22х – 3 ∙ 2х + а2 – 4а = 0 имеет два корня?Решение.Пусть t = 2х, t > 0, t 2 – 3t + (а2 – 4а) = 0 .1) Т. к. уравнение имеет два корня, то D =…2) Т. к. t1, 2 > 0, то t1 ∙ t2 > 0, т. е. а2 – 4а > 0 (?...). Значит, D > 0, −4а2 + 16а + 9 > 0, а2 – 4а > 0; а (а − 4) > 0; … Ответ: а (-0,5; 0) или (4; 4,5).

1. 0,32х + 1 = (3 )2 2. у = 5х – 1 у =3. 5∙2х + 3 − 4∙2х – 1 = 19 4*. 3∙9х = 2∙15х + 5∙25х

Из материалов ЕГЭ 2008 – 2010 годов выбрать задания по теме и решить их. Решить уравнения и систему уравнений:1. (2 )х + 7 = 9/492. у = 3х + 2 у = 3. 2 ∙ 3х + 1 − 4 ∙ 3х – 1 = 424* 2 ∙ 4х − 3 ∙ 10х = 5 ∙ 25х

Показательные уравнения