Презентация на тему: Параллельность прямых в пространстве

параллельность прямых в пространствеВыполнила учитель математики МОУ Поназыревская средняя школа Орлова Н.В.

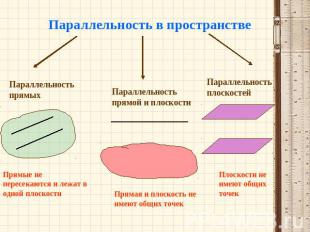
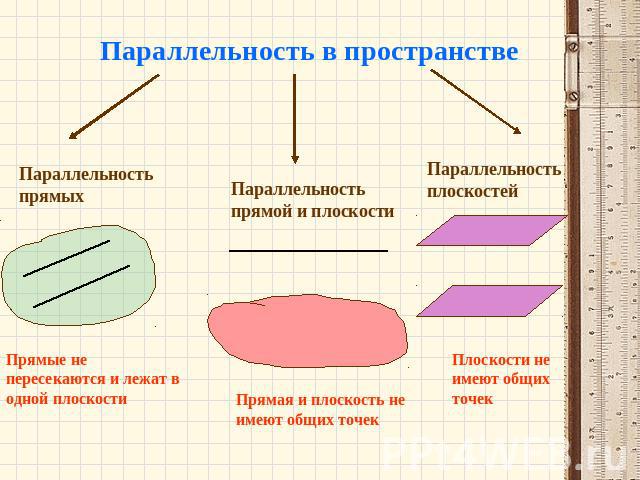
Параллельность в пространствеПараллельность прямыхПараллельность прямой и плоскостиПараллельность плоскостейПлоскости не имеют общих точекПрямая и плоскость не имеют общих точекПрямые не пересекаются и лежат в одной плоскости

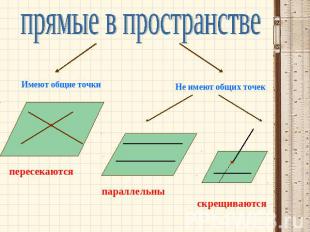
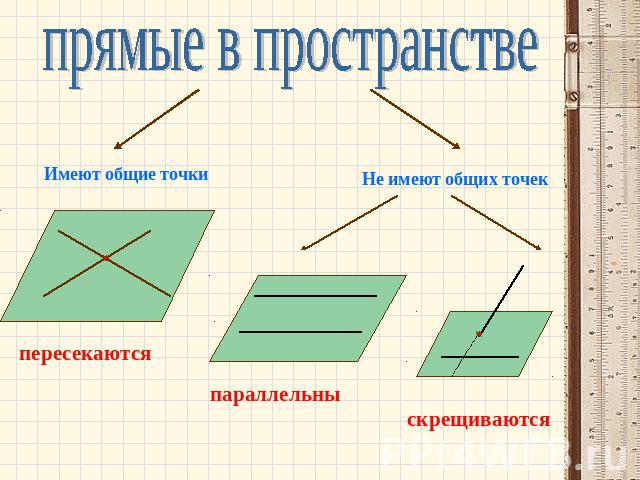
прямые в пространствеИмеют общие точкиНе имеют общих точекпересекаютсяпараллельныскрещиваются

свойство параллельныхпрямых в пространствеТеорема 16.1Через точку вне данной прямой в пространстве можно провести прямую параллельную данной и притом только одну.Дано: прямая а и точка А ¢ аДоказать : существует прямая b || a, b единственна

Доказательство теоремы 16.1По теореме 15.1 построим плоскость α(а,А)По аксиоме планиметрии в данной плоскости через т.А можно провести b || a и притом только По теореме 15.1 плоскость единственна, следовательно прямая b единственна.Теорема доказана.

признак параллельностипрямых в пространстве.Теорема 16.2Если две прямые параллельны третьей прямой, то они тоже параллельныДано: а||b; c||bДоказать : a||c

Доказательство теоремы1. Если a, b, c лежат в одной плоскости смотри теорему 4.1 в планиметрииПусть a, b, c не лежат в одной плоскости Построим плоскости α(a,b) и β(b,c)Поставим точку В на прямой аПостроим плоскость γ(с,В)Пусть d∩b=MMєα,γ, β следовательно по С2 γ∩β =с проходящей через точку М Получаем, c∩b, что противоречит условию, значит d не ∩bЗначит d||b, следовательно d=аc||a, так как они лежат в одной плоскости γ и не пересекаются