Презентация на тему: Открытый урок «Логарифмическая функция»

Логарифмическая функция Функция y=log , а x где a – заданное число, a > 0 , a =1 , называется логарифмической

Область определения логарифмической функции – множество всех положительных чисел Это следует из того,что для любого действительного числа В есть такое положительное число X , что y= log x имеет смысл только при x>0 a 0 x y

Множество значений логарифмической функции – множество r всех действительных чисел. Это следует из того, что для любого действительного числа b есть такое положительное число x, что log x=b. a 0 y x

монотонность а) если x < x ,то log x < log x 1 a б) если log x < log x ,то x >x a 1 Ф. Возрастающая Ф.Убывающая a 2 1 2 a>1 2 1 2 a 0

Если x=1 , то y= log 1=0 (свойство 3) Значит график пересекает ось OX в точке A (1;0). График не переcекает ось OY a

01, и убывающая, если 0

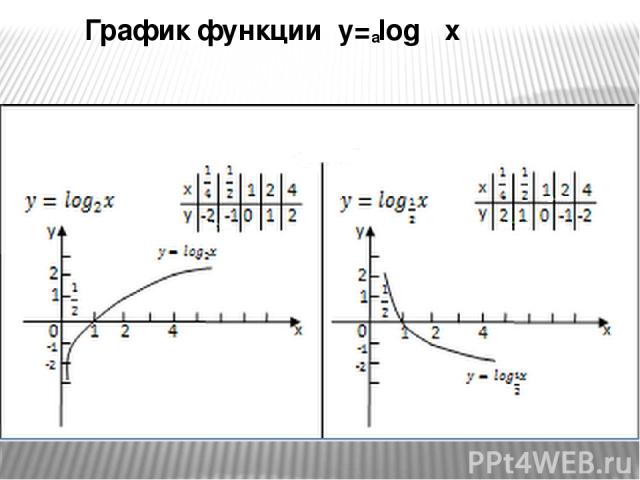
График функции y= log x a