Презентация на тему: Математическая статистика результатов ЕГЭ

Математическая статистика результатов ЕГЭ Выполнила: ученица 10 классаБелогорской ГимназииРеброва НаташаРуководитель: Учитель математики Ягудина Л. Ф.

Актуальность работы следует из того, что аппарат математической статистики является изумительным по мощности и гибкости инструментом для отсеивания закономерностей от случайностей. Исследователю обязательно необходимо накапливать информацию об окружающем мире, пытаясь выделить закономерности из случайностейЦель: исследование результатов ЕГЭ методами математической статистики.Задачи: - Раскрыть понятие математической статистики -Изучить первичные статистические данные результатов ЕГЭ - Сравнить результаты ЕГЭ по годам, с помощью математической статистики - Спрогнозировать результат на 2009 г.

Объект исследования: результаты ЕГЭ по математике по годам учащихся 11 классов Белогорской гимназии.Предмет исследования: методы математической статистики.Методы исследования: - работа с научно-методической литературой; - изучение документации по результатам ЕГЭ; - подсчет; - обработка данных.

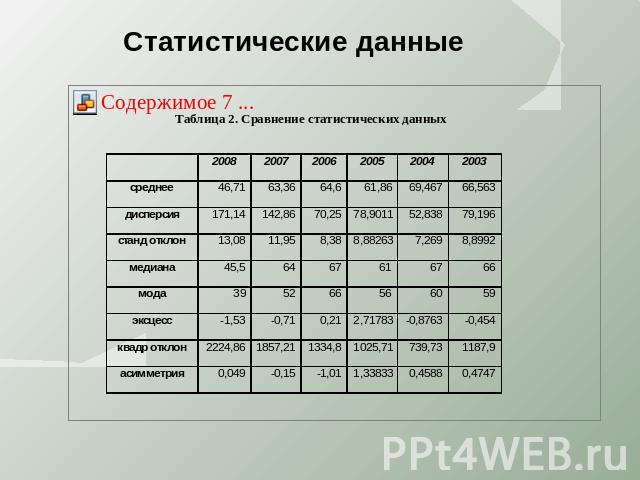
Статистические данные

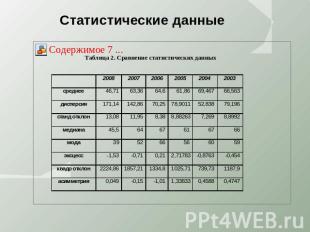
Статистические данные

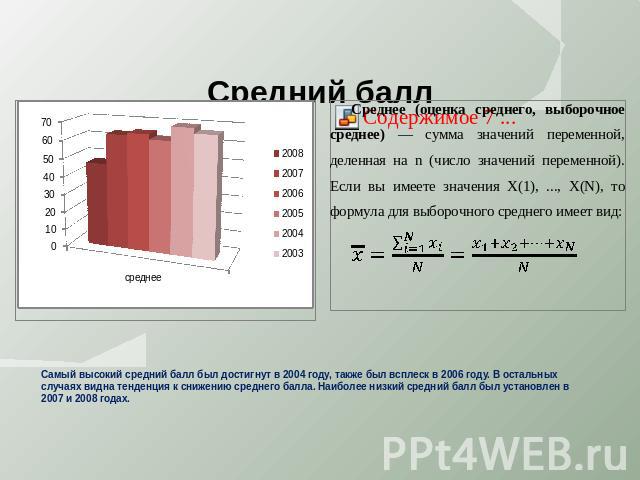
Средний балл Самый высокий средний балл был достигнут в 2004 году, также был всплеск в 2006 году. В остальных случаях видна тенденция к снижению среднего балла. Наиболее низкий средний балл был установлен в 2007 и 2008 годах.

Дисперсия Низкое значение дисперсии характеризует хороший результат. Также как и в предыдущем случае, лучшие показатели были достигнуты в 2004 и 2006 году. В последнее время результаты ухудшаются.

Стандартное отклонение Стандартное отклонение также подтверждает наши предыдущие результаты, 2006 и 2004 годов. Самое большое отклонение имеется в результатах 2006 года.

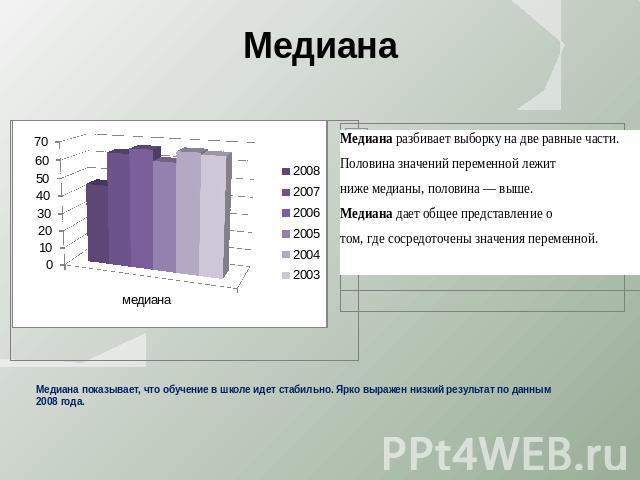
Медиана Медиана показывает, что обучение в школе идет стабильно. Ярко выражен низкий результат по данным 2008 года.

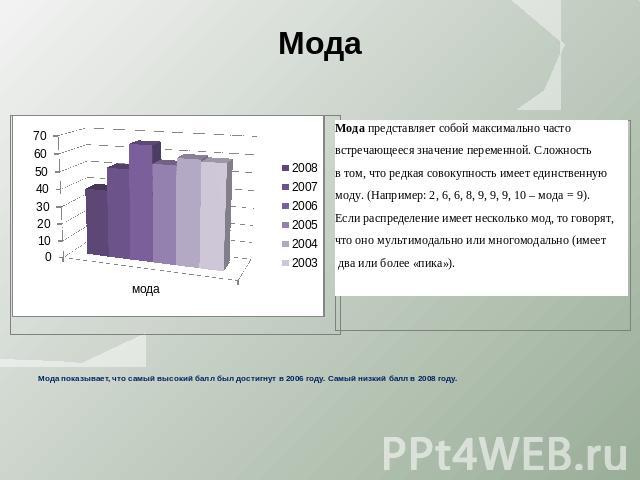
Мода показывает, что самый высокий балл был достигнут в 2006 году. Самый низкий балл в 2008 году.

Эксцесс По диаграмме эксцесса можно сделать вывод, что самый удачный год - 2006г. Самым неудачным относительно значения эксцесса является 2005 год, т. к. результат дал высокое отклонение от 0.

Асимметрия Отрицательная асимметрия видна в результатах 2006 и 2007 гг. Остальные данные асимметрии являются положительными.

Вывод Исследовав результаты сдачи ЕГЭ по математике по годам, наиболее удачными и продуктивными в этом плане являются 2004 и 2006 гг. Самые низкие результаты показали 2007 и 2008 год. В последнее время тенденция идет к снижению знаний учащихся, следовательно, к более низким результатам. Самый высокий средний балл был достигнут в 2004 году, также был всплеск в 2006 году. В остальных случаях видна тенденция к снижению среднего балла. Наиболее низкий средний балл был установлен в 2007 и 2008 годах. Низкое значение дисперсии характеризует хороший результат. Также как и в предыдущем случае, лучшие показатели были достигнуты в 2004 и 2006 году. В последнее время результаты ухудшаются. Стандартное отклонение также подтверждает наши предыдущие результаты, 2006 и 2004 годов. Самое большое отклонение имеется в результатах 2006 года. Медиана показывает, что обучение в школе идет стабильно. Ярко выражен низкий результат по данным 2008 года.

Мода показывает, что самый высокий балл был достигнут в 2006 году. Самый низкий балл в 2008 году. По диаграмме эксцесса можно сделать вывод, что самый удачный год - 2006г. Самым неудачным относительно значения эксцесса является 2005 год, т. к. результат дал высокое отклонение от 0. В 2008 году произошло снижение вторичного балла за экзамен, т. е. за такое же количество заданий которое было предусмотрено в 2007 году, давали меньшее количество баллов. Этот факт не учитывался в ходе подсчетов. Следовательно, результат в 2008 году может быть выше, чем это отражено в работе. По данным результатам виден прогноз результатов ЕГЭ в этом году. По статистике планируется более низкий результат, но эту ситуацию можно переломить, если учащиеся будут серьезно готовится к экзаменам.

Математика. Т.2. – М.,2003 – (Энциклопедия «Аванта»)Бунимович Е. А., Булычев В. А. Вероятность и статистика в курсе математики общеобразовательной школы. – М., 2005Соколов Г. А. Математическая статистика. – М., 2007Манита А. Д. Теория вероятностей и математическая статистика. – М., 1995Архивные данные.