Презентация на тему: Комбинаторные задачи в 5 - 6 классах

Комбинаторные задачи 5 – 6 класс Учитель математики МБОУ «Гимназия» г. Новозыбкова Арещенко Елена Александровна

Комбинаторика раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов

КОМБИНАТОРНАЯ ЗАДАЧА – это задача, требующая осуществления перебора всех возможных вариантов или подсчета их числа.

Решить комбинаторную задачу - это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи.

ОРГАНИЗОВАННЫЙ ПЕРЕБОР – строгий порядок разбора всех случаев, возможных решений.

Решение задачи методом полного перебора всех возможных вариантов №1 Сколько двузначных чисел можно составить, используя цифры 1; 4; 7? Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания: 11;14;17;(начали с 1) 41;44;47;(начали с 4) 71;74;77;(начали с 7) Таким образом, из трёх данных цифр можно составить всего 9 различных двузначных чисел. Ответ: 9 чисел.

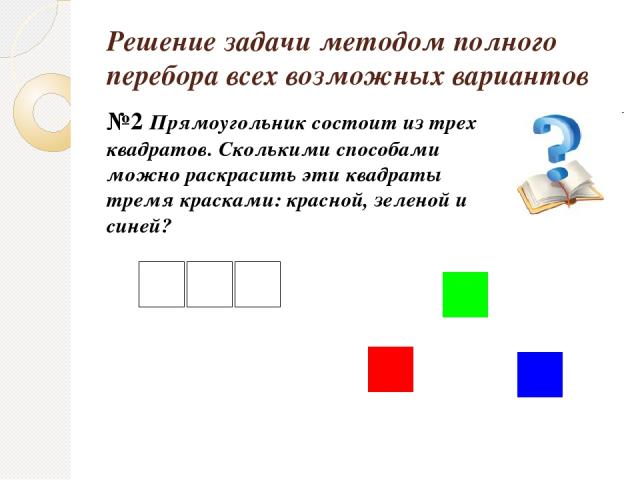
Решение задачи методом полного перебора всех возможных вариантов №2 Прямоугольник состоит из трех квадратов. Сколькими способами можно раскрасить эти квадраты тремя красками: красной, зеленой и синей?

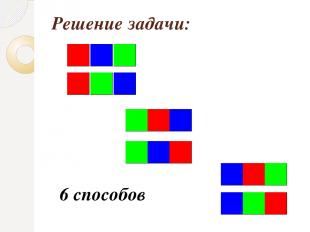
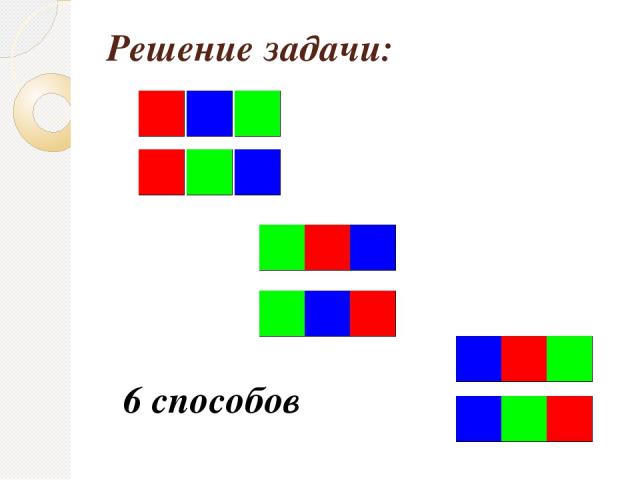
Решение задачи: 6 способов

Решение задач с помощью дерева возможных вариантов Существует более общий подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название - дерево возможных вариантов. При правильном построении дерева ни один из возможных вариантов решения не будет потерян.

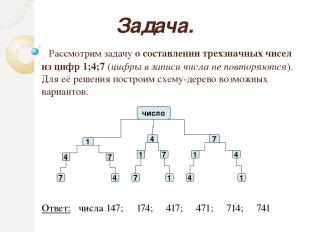
Задача. Рассмотрим задачу о составлении трехзначных чисел из цифр 1;4;7 (цифры в записи числа не повторяются). Для её решения построим схему-дерево возможных вариантов. число 1 4 7 4 7 7 4 1 7 7 1 1 4 4 1 Ответ: числа 147; 174; 417; 471; 714; 741

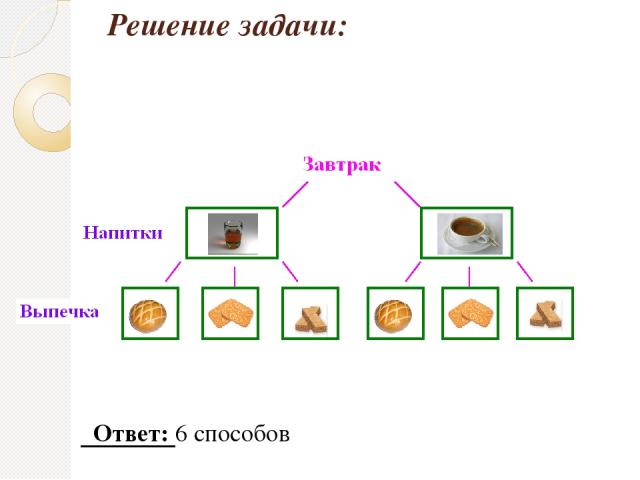
Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая, кофе, булочки, печенья и вафель?

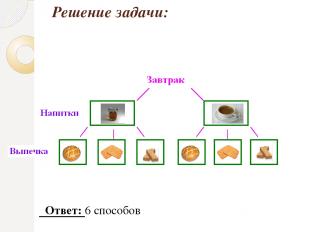
Решение задачи: Ответ: 6 способов

Правило умножения в комбинаторных задачах. Для комбинаторной задачи с умножением можно построить дерево вариантов, но такое дерево строить станет намного сложнее, именно поэтому используется метод умножения, чтобы запись была короче. Рассмотрим этот метод на примере одной задачи: На обед в школьной столовой предлагается 2 вида супа, 3 вторых блюда и 4 разных сока. Сколько различных обедов можно составить по предложенному меню? Рассуждение: Первое блюдо можно выбрать 2 способами, для каждого вида супа можно выбрать второе блюдо из трёх предложенных, уже получается 6 вариантов , осталось выбрать напиток: для каждого из 6 полученных наборов существует 4 способа выбора напитка. Итог: 24 способа.

Оформление: Суп - 2 способа Вторые блюда - 3 способа Сок - 4 способа Решение: 2 x 3 x 4= 24 Ответ: Можно составить 24 варианта различных обедов

Перестановки в комбинаторных задачах. В комбинаторике часто приходиться решать задачу о том, сколькими способами можно расположить в ряд или, как говорят математики, упорядочить все элементы некоторого множества. Каждое из таких расположений называют перестановкой.

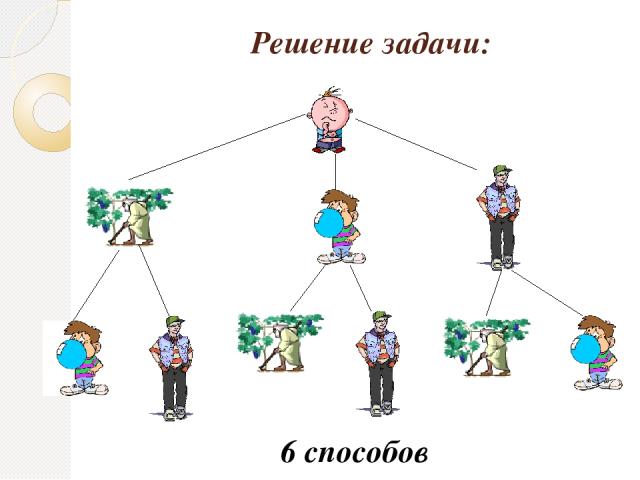
Миша решил в воскресенье навестить дедушку, своего друга Петю и старшего брата Володю. В каком порядке он может организовать визиты? Сколько вариантов получилось ?

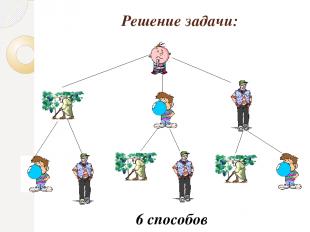
Решение задачи: 6 способов

Здесь речь идет о числе перестановок, т.е. о выполнении трех визитов в разной последовательности. Сначала Миша выбирает, к кому отправится в первую очередь – 3 способа, затем он идет в гости к кому – то из 2 оставшихся, ну а затем – к последнему. 3•2•1= 6 способов

Задача. В турнире участвуют четыре человека. Сколькими способами могут быть распределены места между ними? Решение. Первое место может занять любой из 4 участников. При этом второе место может занять любой из трёх оставшихся, третье – любой из двух оставшихся, а на четвёртом месте остаётся последний участник. Значит, места между участниками могут быть распределены следующим образом 4•3•2•1=24. Ответ: 24 способами.

Заметим, что в решении каждой задачи получили произведение всех натуральных чисел от 1 до 3 ( в первой задаче) до 4 ( во второй задаче) Такое произведение записывается короче: 3•2•1 = 3! ( «три факториал») 4•3•2•1=4! ( «четыре факториал»)

Андрей, Боря, Витя и Дима решили покататься на карусели. На ней было 4 сиденья с изображением льва, слона, тигра и медведя. Ребята заспорили, кому где сидеть, поэтому решили перепробовать все способы. Сколько раз нужно в таком случае прокатиться на карусели? Решение: Здесь речь идет о числе перестановок, т.е. о размещении 4 мальчиков по 4 местам разными способами: 4! = 24