Презентация на тему: Комбинаторика

Сидоренко Ольга группа «СО-11»

Введение Комбинато рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике). Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Основные формулы комбинаторики Перестановки: Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения, а их число равно Pn = n! = 1·2·3…·(n – 1)·n Символ n! называется факториалом и обозначает произведение всех целых чисел от 1 до n. По определению, считают, что 0!=1, 1!=1 Пример всех перестановок из n = 3 объектов (различных фигур) - на картинке справа.  Согласно формуле, их должно быть ровно P3 = 3! = 1·2·3 = 6 так и получается. С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов - уже 3628800 (больше 3 миллионов!).

Размещения Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком, а их число равно Anm = = n·(n – 1)·…·(n – m + 1) Пример всех размещений из n = 3 объектов (различных фигур) по m = 2  на картинке справа. Согласно формуле, их должно быть ровно A32 = 3·(3 – 2 + 1) = 3 · 2 = 6

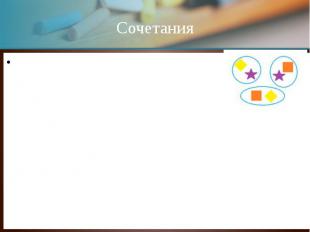
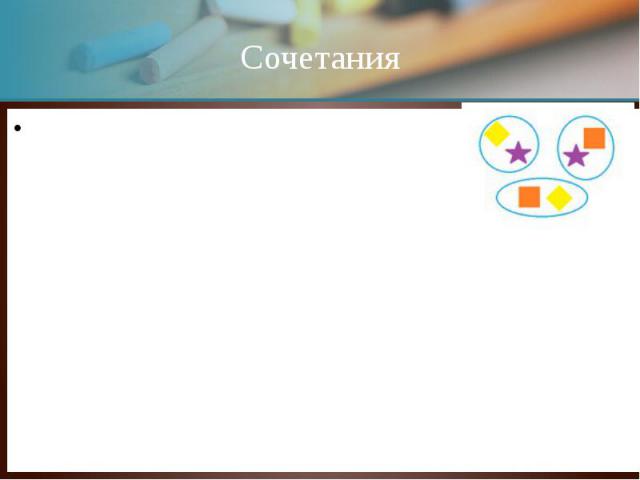
Сочетания Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом, а их число равно Cnm = Пример всех сочетаний из n = 3 объектов (различных фигур) по  m = 2 на картинке справа. Согласно формуле, их должно быть ровно C32 = = 3

Перестановки. Задача

Сочетания. Задача

Размещения. Задача

Спасибо за просмотр!