Презентация на тему: Функции, их свойства и графики

Государственное бюджетное образовательное учреждениелицей № 1547 г. Москва Работа выполнена:Емельяненко Святославом,(ученик 9 «А» класс)Руководитель:учитель математики Карпова Светлана Владимировна2012 год

Функции,их свойства и графики

Темы:Функция.Использования функций в физике.Свойства функций.Квадратичная функция.Преобразование графиков функций.

Свойства функцийВозрастание и убывание функций.Свойства монотонных функций.Четные и нечетные функции.Ограниченные и неограниченные функции.

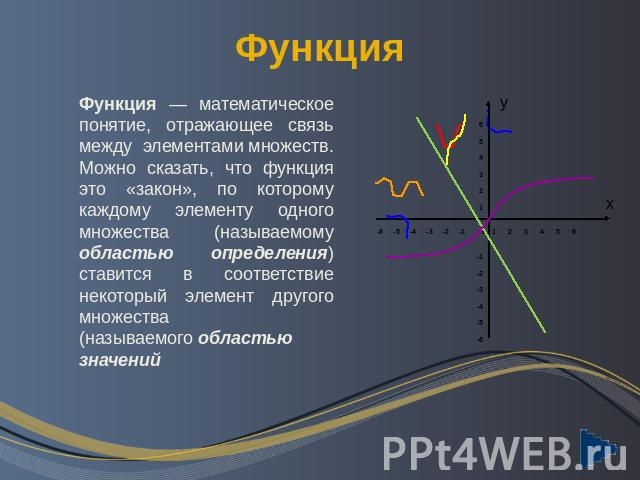
Функция Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений

Функция

Пример:Волновая функция, или пси-функция — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису , так же функции используют для графического показания волновых колебаний звука.

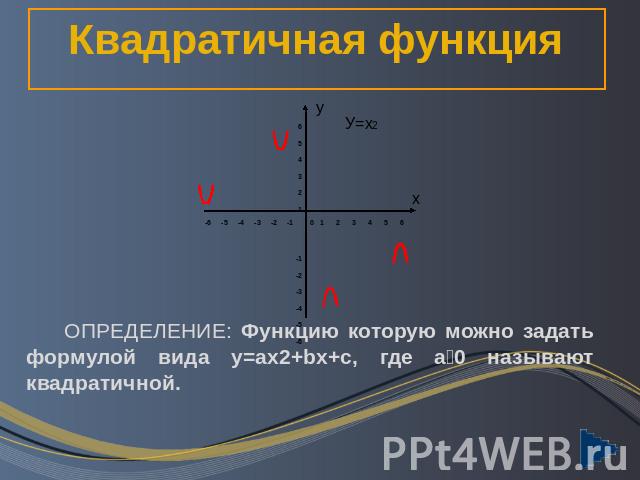
Квадратичная функция ОПРЕДЕЛЕНИЕ: Функцию которую можно задать формулой вида y=ax2+bx+c, где а0 называют квадратичной.

Квадратичная функция При а1 (a0), b=c=0, квадратичная функция имеет вид y=ax2 График – парабола. Свойства функции:D(y)=R (симметричное множество).Функция четная т.к. y(-x) = y(x). Ось симметрии x=0.Если х=0, то у=0. т.е проходит через начало координат (0,0).Если х > 0,то у>0; если x<0, то у>0.Функция возрастает на [0; ∞), убывает (- ∞;0].6. E(y)= [0; ∞).7. Yнаим=0.8. Ограничена снизу.

Квадратичная функция При а1 (a0), b=c=0, квадратичная функция имеет вид y=ax2 График – парабола. Свойства функции:D(y)=R (симметричное множество).Функция четная т.к. y(-x) = y(x). Ось симметрии x=0.Если х=0, то у=0. т.е проходит через начало координат (0,0).Если х > 0,то у0; если x<0, то у0.Функция возрастает на (-∞;0, убывает [∞;0).6. E(y)= (∞;0].7. Yнаим=0.8. Ограничена сверху.

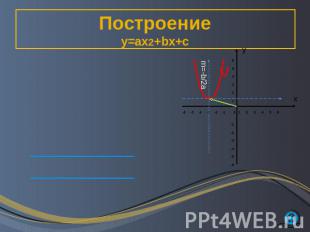
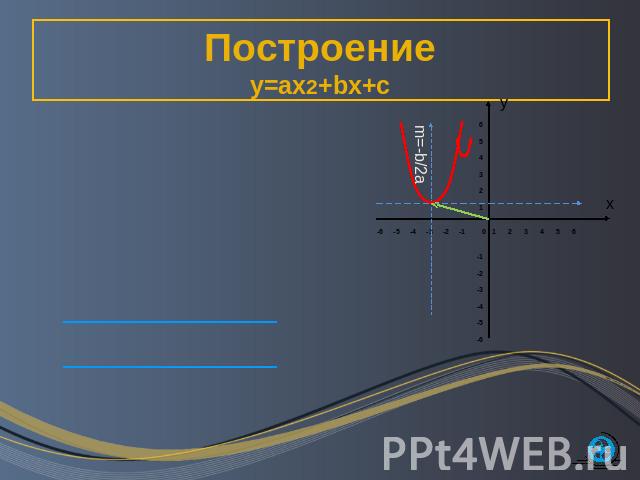
Построениеy=ax2+bx+c y=ax2+bx+c (1) y=a(x-m)2+n (2)(Выделив квадрат двучлена)m=−b/2a, n=D/4aГрафик функции (1) можно получить из графика y=ax2 с помощью двух параллельных переносов.Вдоль оси х на m единиц, (m<0 влево, m>0 вправо). Вдоль оси у на n единиц , (n<0 вниз, n>0 вверх)

Преобразование графиков функций Растяжение и сжатие графиков функций к оси ординат.Графики функций y=|f(x)| и y=f(|x|).

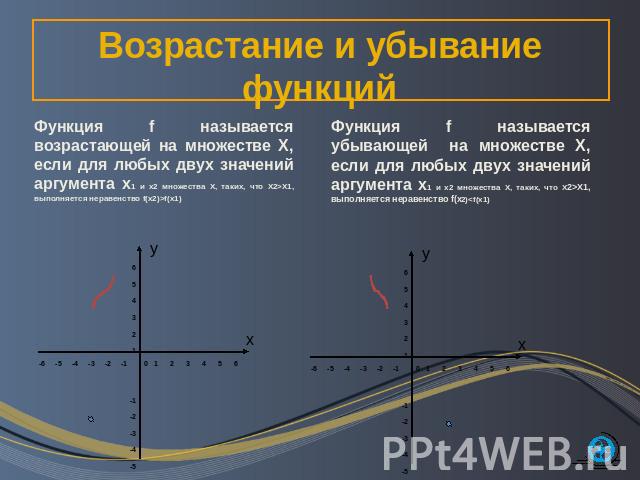
Возрастание и убывание функций Функция f называется возрастающей на множестве Х, если для любых двух значений аргумента х1 и х2 множества Х, таких, что Х2>X1, выполняется неравенство f(x2)>f(x1) Функция f называется убывающей на множестве Х, если для любых двух значений аргумента х1 и х2 множества Х, таких, что Х2>X1, выполняется неравенство f(x2)<f(x1)

Свойства монотонных функций Монотонная функция каждое свое значение принимает лишь при одном значении аргумента.Если функция y=f(x) является возрастающей (убывающей), то функция y=-f(x) является убывающей (возрастающей).Сумма двух возрастающих функций является возрастающей функцией, а сумма двух убывающих функций является убывающей функцией.Если обе функции f и g возрастающие или обе убывающие, то функция ф(х)=f(g(x))- возрастающая функция.Если функция y=f(x) монотонная на множестве Х и сохраняет на этом множестве знак, то функция g(x)=1:f(x) на множестве Х имеет противоположный характер монотонности.

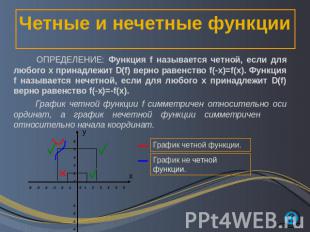
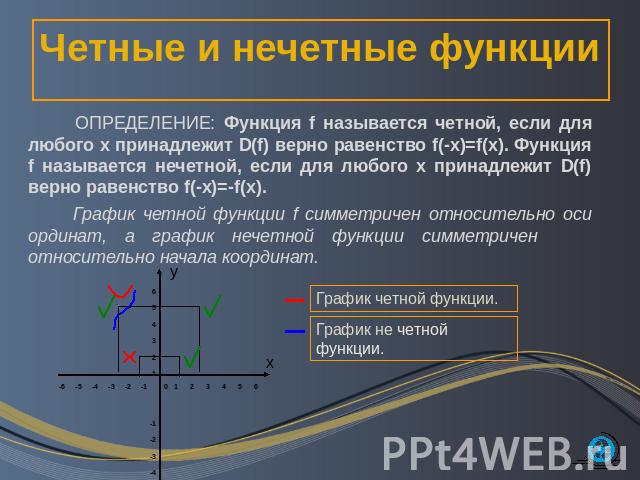
Четные и нечетные функции ОПРЕДЕЛЕНИЕ: Функция f называется четной, если для любого х принадлежит D(f) верно равенство f(-x)=f(x). Функция f называется нечетной, если для любого х принадлежит D(f) верно равенство f(-x)=-f(x). График четной функции f симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

Ограниченные и неограниченные функции ОПРЕДЕЛЕНИЕ: Функция называется ограниченной, если существует два числа а и b такие, что для любого аргумента х и y выполняется неравенство a f(x) b.

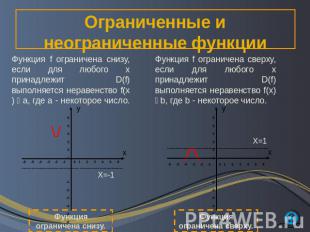
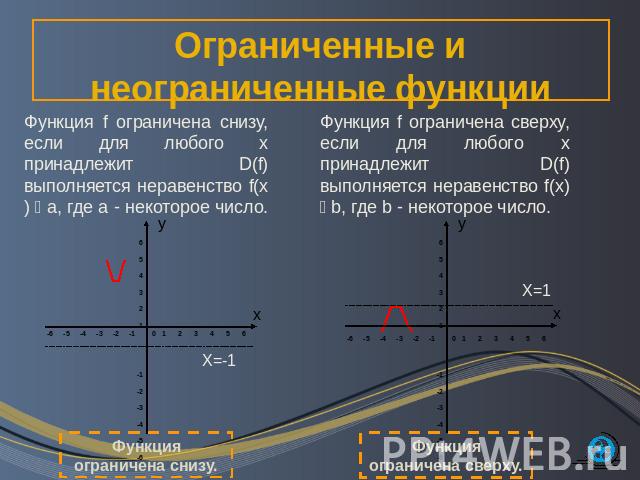
Ограниченные и неограниченные функции Функция f ограничена снизу, если для любого х принадлежит D(f) выполняется неравенство f(x) а, где а - некоторое число. Функция f ограничена сверху, если для любого х принадлежит D(f) выполняется неравенство f(x) b, где b - некоторое число. Функция ограничена снизу. Функция ограничена сверху.

Растяжение и сжатие графиков функций к оси ординат График функции y = k f (x) при k > 1 можно получить из графика функции y = f (x) растяжением от оси x исходного графика в k раз, а при 0 < k < 1 - сжатием к оси x графика функции y = f (x) в 1/k раз. График функции y = f (k x) получается из графика функции y = f (x) сжатием в k раз к оси OY при k > 1 и растяжением в 1/k   раз от оси OY при 0 < k < 1.При k = 1 исходный и конечный графики совпадают. При k < 0 график не только растягивается (сжимается), но и отражается относительно оси OY.

График функций y=|f(x)| Построить y=|f(x)|Оставить без изменений ту часть графика функции y=f(x), где f(x)0,Вместо участков графика функции y=f(x), где f(x)<0, построить их зеркальное отражение относительно оси х.

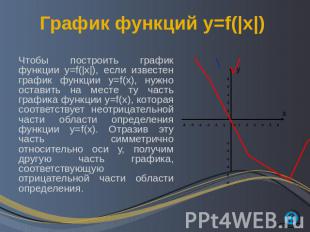
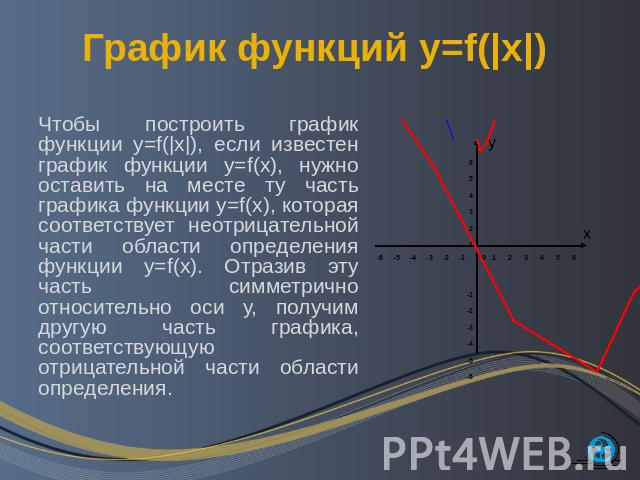
График функций y=f(|x|) Чтобы построить график функции y=f(|x|), если известен график функции y=f(x), нужно оставить на месте ту часть графика функции y=f(x), которая соответствует неотрицательной части области определения функции y=f(x). Отразив эту часть симметрично относительно оси у, получим другую часть графика, соответствующую отрицательной части области определения.

Информация Стиль оформления взят с бесплатного интернет ресурса microsoft.com Список литературы: Ю.Н.Макарычев Алгебра. 9 класс. – Мнемозина, 2010