Презентация на тему: четырехугольники2

Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 7» Автор: Данилов Н., Игнатьева К., учащиеся 8 Б класса Мирный, 2015 Четырехугольники

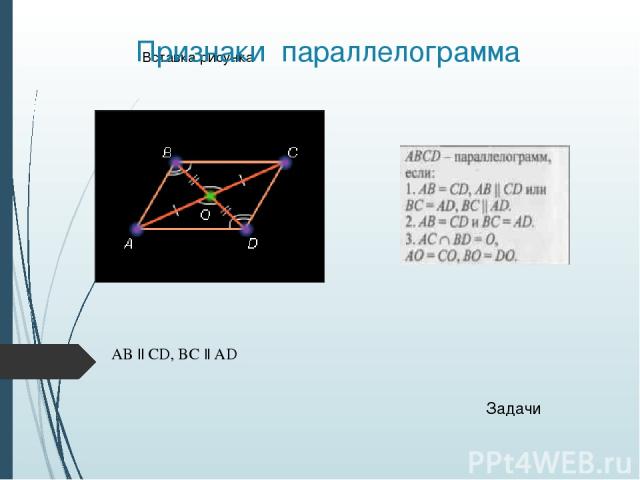
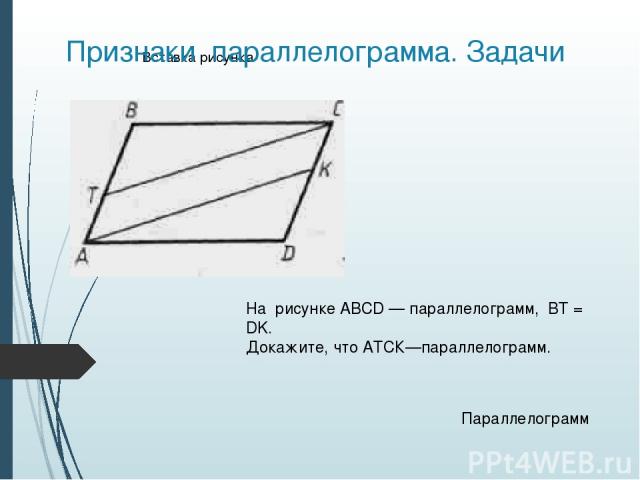
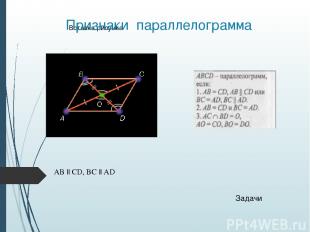
Параллелограмм Четырехугольник, у которого противоположные стороны параллельны, называется параллелограммом Свойства Признаки

Смежными являются стороны: [AB] и [CB], [BC] и [CD], [CD] и [AD], [AB] и [AD]. Каждая пара: [AB] и [CD], [BC] и [AD] – содержит противолежащие стороны. Четыре пары вершин: A и B, B и C, C и D, A и D – содержат все возможные соседние вершины четырехугольника. Пара вершин A и C (B и D ) являются противолежащими. Стороны, исходящие из одной вершины, называются смежными. Вершины, являющиеся концами одной стороны, называются соседними. Стороны, не имеющие общих вершин, называются противолежащими. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины, называются диагоналями.

Параллелограмм Четырехугольник, у которого противоположные стороны параллельны, называется параллелограммом Свойства Признаки

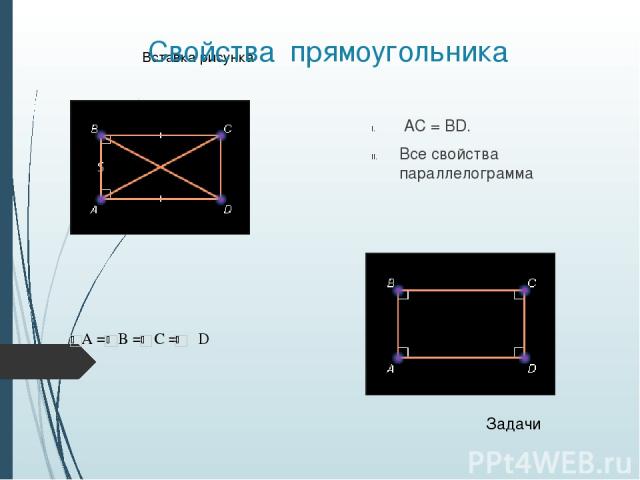
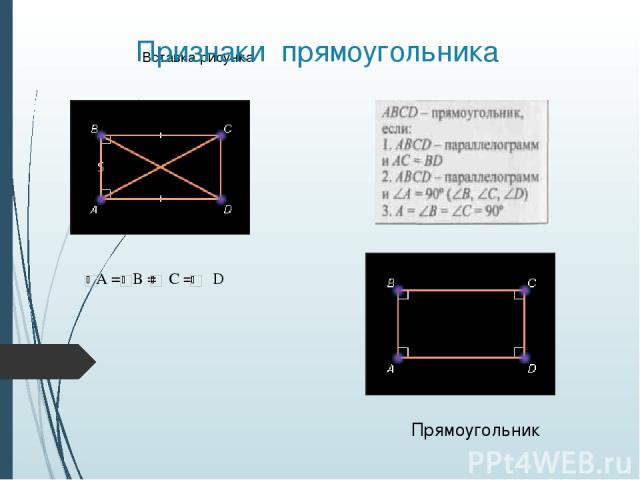
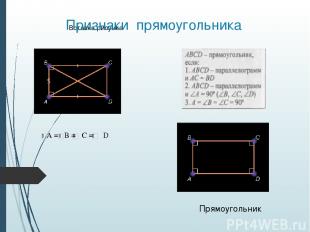
Прямоугольник Параллелограмм, у которого все углы прямые, называется прямоугольником Свойства Признаки

Прямоугольник Параллелограмм, у которого все углы прямые, называется прямоугольником Свойства Признаки

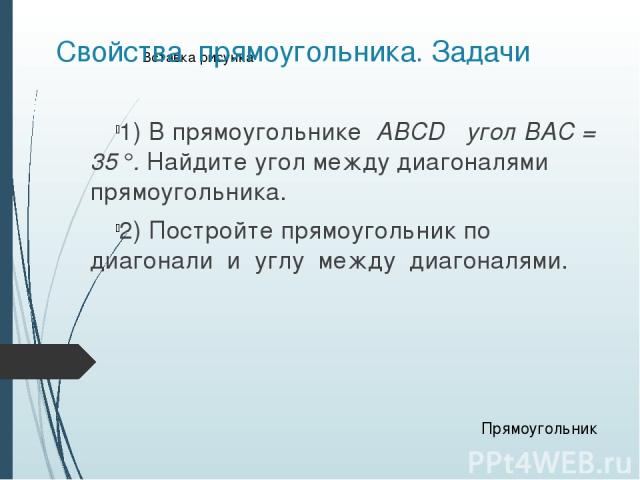
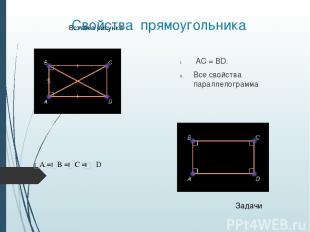
Свойства прямоугольника. Задачи 1) В прямоугольнике ABCD угол BAC = 35°. Найдите угол между диагоналями прямоугольника. 2) Постройте прямоугольник по диагонали и углу между диагоналями. Прямоугольник

Свойства и признаки квадрата. Задачи Квадрат Внутри квадрата ABCD взята точка K и на отрезке АК как на стороне построен квадрат AKLM, у которого сторона KL пересекает сторону AD. Докажите, что отрезки ВК и DM равны. 2) ABCD — квадрат, точка М принадлежит стороне CD, АК — биссектриса угла ВАМ (К ВС). Докажите, что AM = BK + DM.

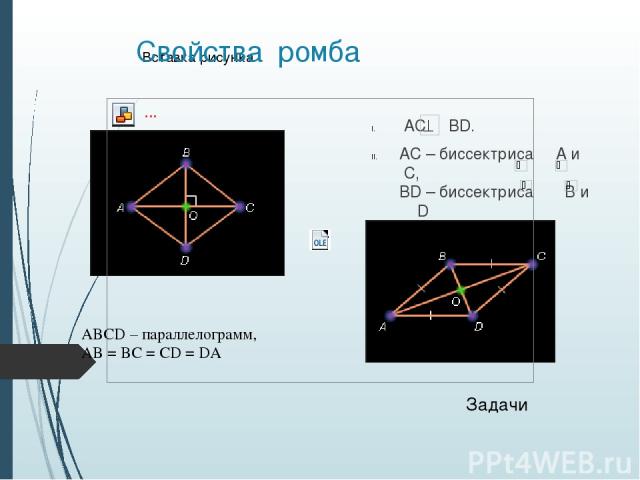
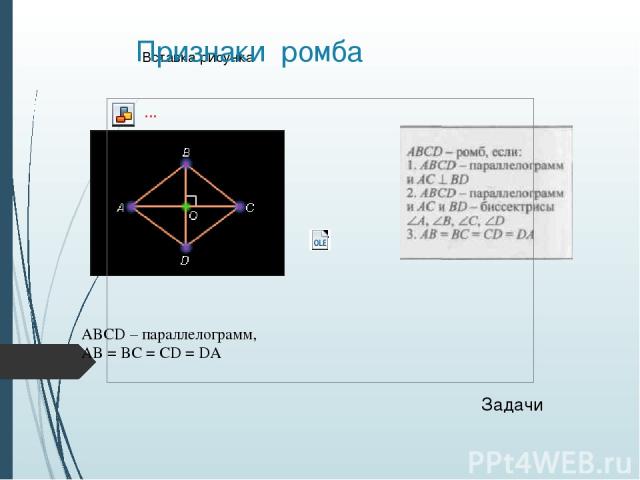
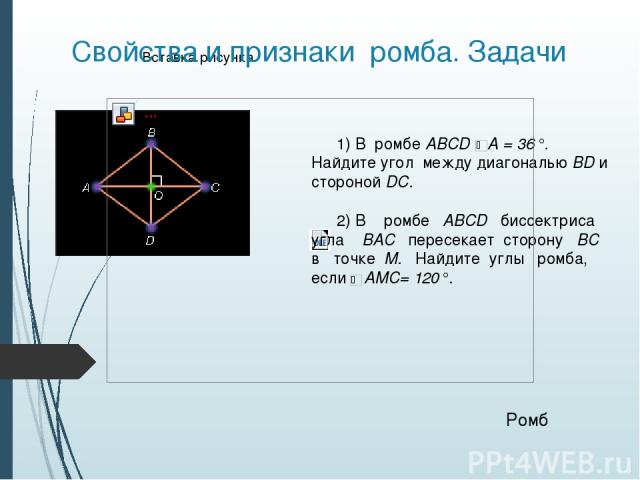
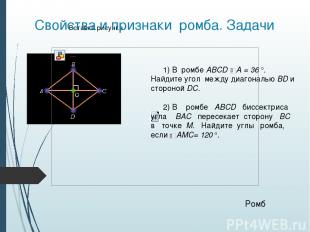
Свойства и признаки ромба. Задачи Ромб 1) В ромбе ABCD А = 36°. Найдите угол между диагональю BD и стороной DC. 2) В ромбе ABCD биссектриса угла ВАС пересекает сторону ВС в точке М. Найдите углы ромба, если АМС= 120°.

Трапеция Четырехугольник, у которого две противоположные стороны параллельны, а две другие – непараллельные, называется трапецией

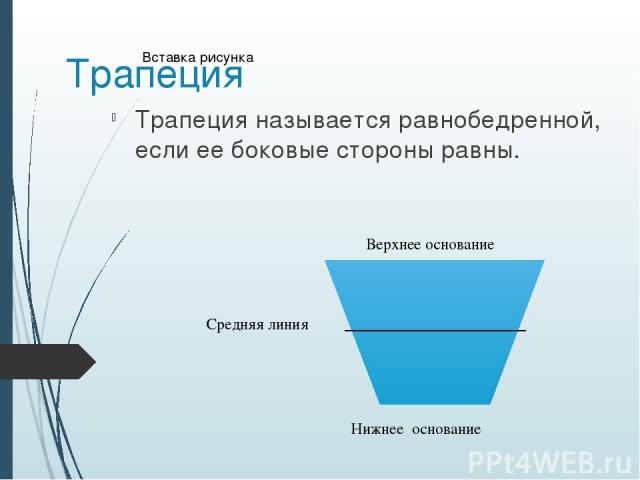
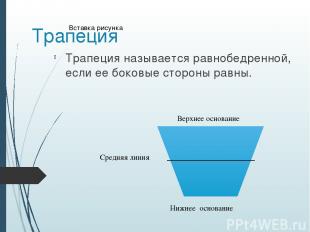
Трапеция Трапеция называется равнобедренной, если ее боковые стороны равны. Верхнее основание Нижнее основание Средняя линия

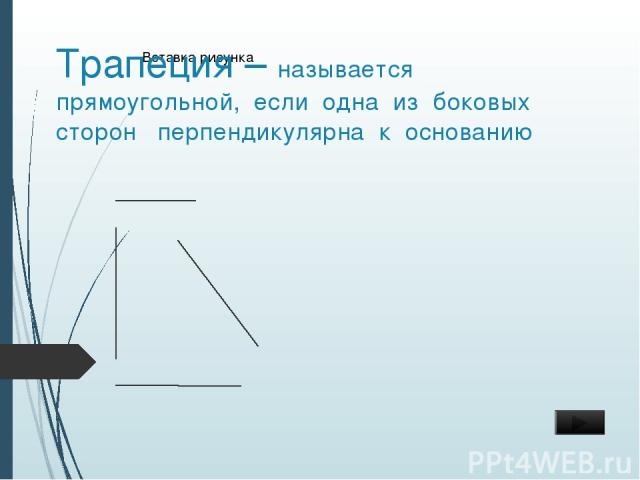
Трапеция – называется прямоугольной, если одна из боковых сторон перпендикулярна к основанию

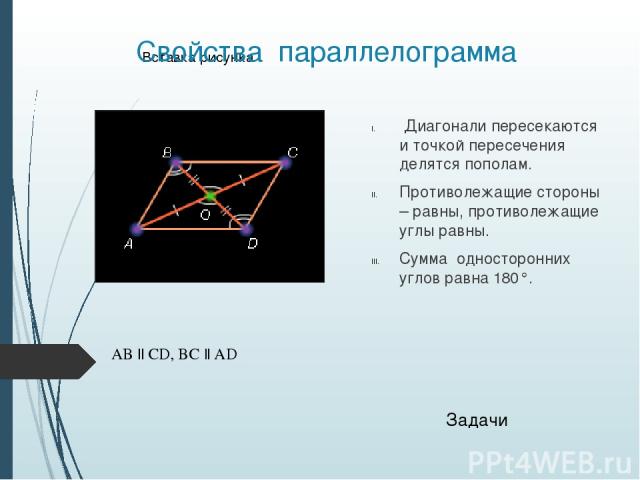
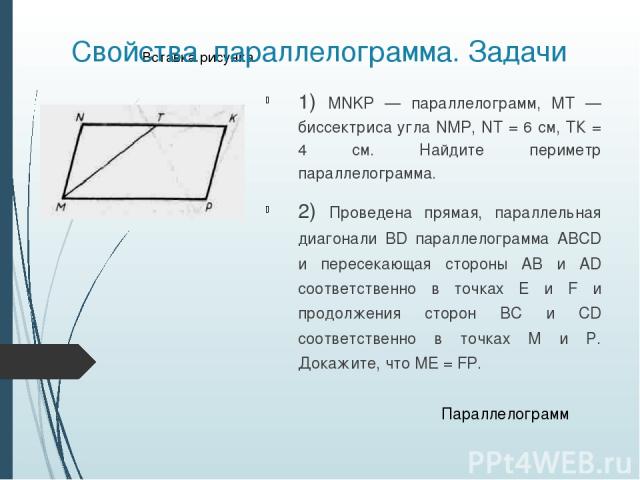
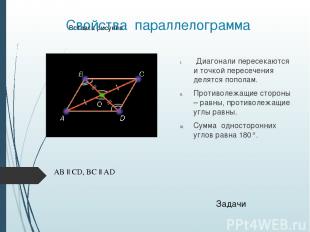
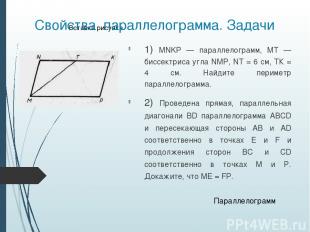
Свойства параллелограмма Диагонали пересекаются и точкой пересечения делятся пополам. Противолежащие стороны – равны, противолежащие углы равны. Сумма односторонних углов равна 180°. AB || CD, BC || AD Задачи