Презентация на тему: Законы алгебры логики

1.6.2 Законы алгебры логики.

Логическая формула-это выражение, содержащее логические константы, логические переменные, знаки логических операций. Логическая функция – зависимость значения одной переменной логической величины от других независимых логических величин аргументов. Таблица истинности – перечень значений функции для всех сочетаний значений аргументов. Содержит 2 в степени n строк – где n число аргументов.

Рассмотрим пример равносильных высказываний 1. Квадратное уравнение имеет действительные корни тогда и только тогда, когда его дискриминант положительный. 2. Если квадратное уравнение имеет действительные корни, то его дискриминант положительный и если дискриминант квадратного уравнения положительный, то оно имеет действительные корни.

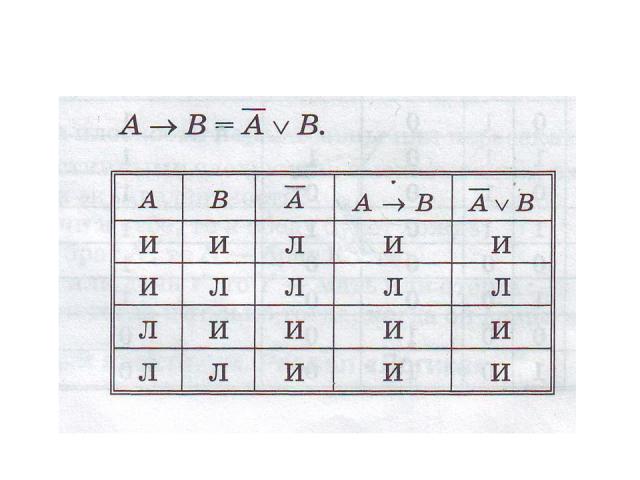
= (1) Соотношение (1) является тождеством двух логических формул. Каким способом можно доказать справедливость равенства?

Построим таблицу истинности

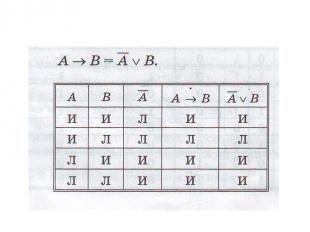
Таким образом получаем: Это выражение закона алгебры логики, сводящего операцию эквивалентности к последовательности операций отрицания, дизъюнкции и конъюнкции.

Любую логическую формулу путем тождественных преобразований можно привести к формуле, содержащей только операции отрицания, дизъюнкции и конъюнкции. Такой способ представления логической формулы называется нормальной формой.

Пример: Шахматы Есть 4 друга: Антон, Виктор, Семен и Дмитрий. Относительно их умение играть в шахматы, справедливы следующие высказывания: Семен играет в шахматы Если Виктор не играет в шахматы, то играет Семен и Дмитрий Если Антон или Виктор играет, то Семен не играет. Преобразуем эти высказывания к алгебраической форме. Введем логические переменные для обозначения четырех простых высказываний: А = «Антон играет в шахматы» В = «Виктор играет в шахматы» С= «Семен играет в шахматы» D = «Дмитрий играет в шахматы»

Давайте узнаем кто же играл в шахматы.

Домашнее задание №4,5,6 стр.108