Презентация на тему: Основные законы алгебры логики

ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ Учитель информатики отделения основного общего образования ГОБУ СПО ВО «Бутурлиновский механико-технологический колледж» г.Бутурлиновка Вылегжанина Татьяна Викторовна

Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия)

В основе современной логики лежат учения, созданные древнегреческими мыслителями (Аристотель, Геродот) Аристотель 384-322 до н.э Геродот ок 490-425 до н.э

ЛОГИКА – наука о формах и способах мышления

Законы мышления отражают в сознании человека свойства, связи и отношения объектов окружающего мира

Высказывание Понятие Умозаключение

Высказывание –логическое выражение, истинность которого требуется доказать

Высказывание не может быть выражено повелительным или вопросительным предложением

Высказывание имеет 2 значения: ложь – (false) – 0 истина – (true) - 1

Высказывание – обозначается большими буквами латинского алфавита (А, В, С)

ЛОГИЧЕСКИЕ ОПЕРАЦИИ

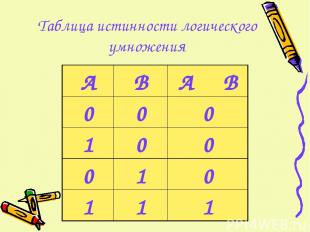
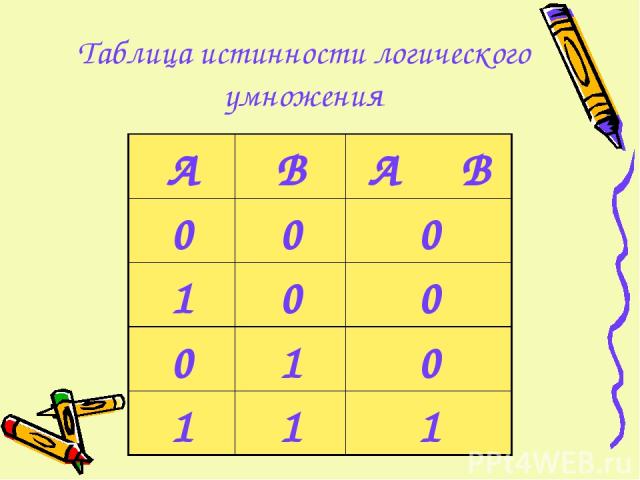
Таблица истинности логического умножения

Дизъюнкция (логическое сложение) читается обозначается А ν B Дизъюнкция истинна, когда хотя бы одно высказывание истинно ИЛИ

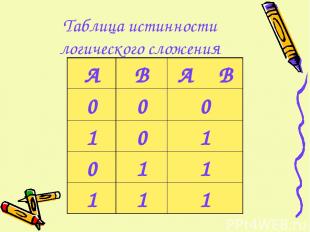
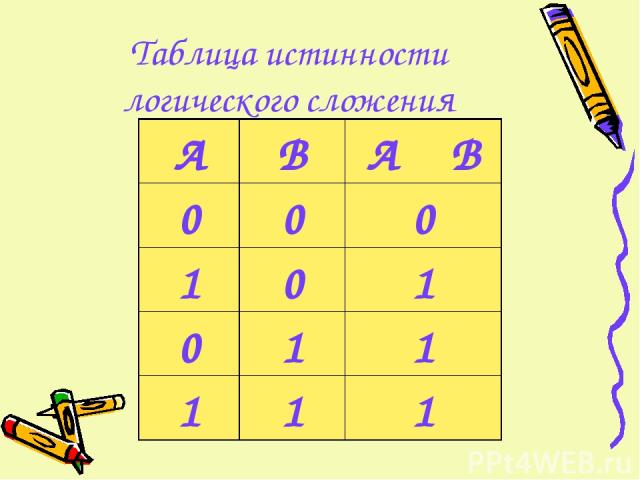
Таблица истинности логического сложения

Инверсия (логическое отрицание) читается обозначается А (не А) НЕ

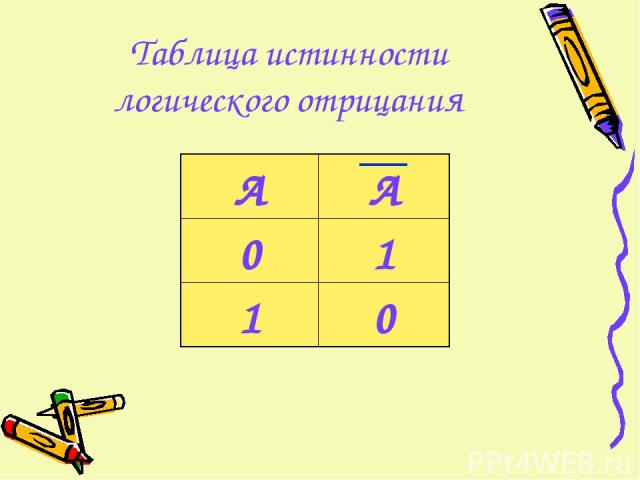
Таблица истинности логического отрицания

Импликация (логическое следование) обозначается А B Импликация ложна, тогда и только тогда, когда из истины следует ложный вывод

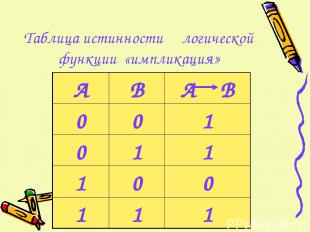
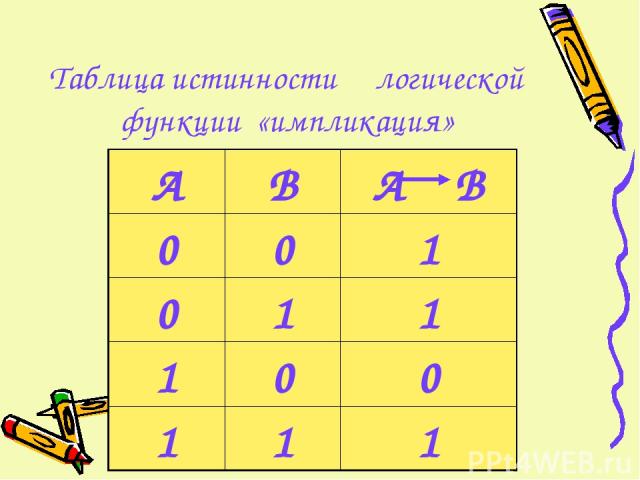
Таблица истинности логической функции «импликация»

Эквивалентность (логическое равенство) обозначается А ~ B Эквивалентность истинна, тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны

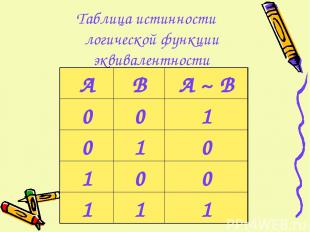
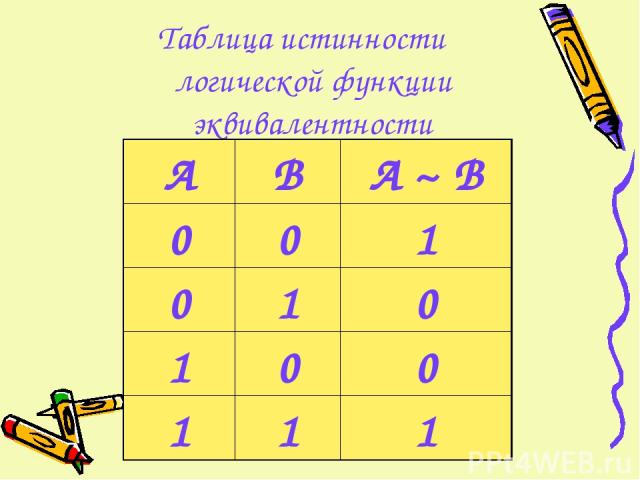
Таблица истинности логической функции эквивалентности

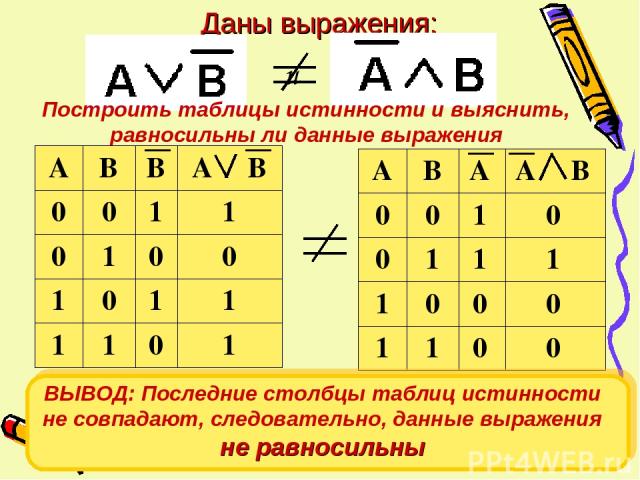
Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными

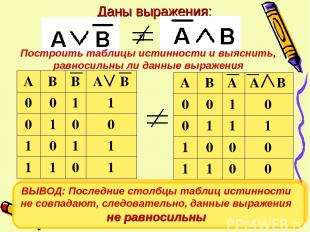
Даны выражения: и Построить таблицы истинности и выяснить, равносильны ли данные выражения

Список источников 1. Учебник «Информатика и ИКТ» Семакин И.Г., изд. Москва «БИНОМ», 2014 г. 2. Изображение: Древний Восток: http://www.yana.kiev.ua/img/resortsb/1965387912.jpg http://apxeo.info/wp-content/uploads/2012/07/pers.jpg Аристотель: http://modafix.ru/images/arist1.jpg Геродот: http://www.stadtwanderer.net/media/sherodot.jpg Логика: http://gcvhf.biz/images/55daf80fc2ffc.jpg http://www.stihi.ru/pics/2011/04/05/3574.gif