Презентация на тему: Параметрическое линейное программирование

Параметрическое линейное программирование Выполнила: студентка 3 курса, группы ММ-61 Лучинина Екатерина Проверил: Щиканов Алексей Юрьевич

Сущность задачи параметрического ЛП Параметрическое линейное программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров. С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.

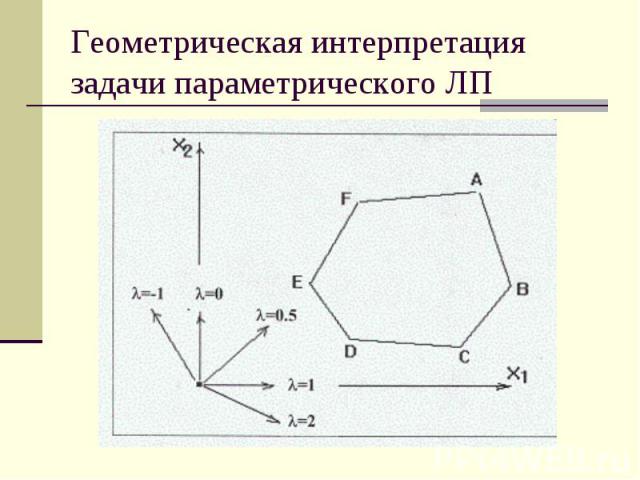
Геометрическая интерпретация задачи параметрического ЛП Если обратиться к геометрической интерпретации задачи, то можно заметить, что вектор-градиент линейной формы определяется её параметром. Например, для целевой функции L(X, λ) = λX1 + (1-λ)X2 при различных значениях параметра λ градиент определяет различные направления роста функции. Нетрудно видеть, что, если при некотором значении параметра максимум достигается в вершине A, то небольшая вариация этого значения несколько изменит направление градиента, но не изменит положение точки максимума. Отсюда напрашивается вывод, что некоторый план, оптимальный при λ = λ0 оптимален и в окрестности λ0, т.е. при α ≤ λ ≤ β где λ0   [α, β].

Геометрическая интерпретация задачи параметрического ЛП

Алгоритм решения задачи параметрического ЛП Считая значение параметра равным некоторому числу , находим оптимальный план Х* или устанавливаем неразрешимость полученной задачи линейного программирования. Определяют множество значений параметра , для которых найденный оптимальный план является оптимальным или задача неразрешима. Эти значения параметра исключаются из рассмотрения. Полагают значение параметра равным некоторому числу, принадлежавшему оставшейся части промежутка, и находят решение полученной задачи линейного программирования. Определяют множество значений параметра , для которых новый оптимальный план остается оптимальным или задача неразрешима. Вычисления повторяются до тех пор, пока не будут исследованы все значения параметра .

Пример задачи параметрического ЛП Предприятие должно выпустить два вида продукции А и В, для изготовления которых используется три вида сырья, нормы расходов заданы в таблице. Известно, что цена на А единицу продукции может изменяться от 2 до 12 у.е., для В от 13 до 3 у.е. Найти оптимальные планы выпуска для заданных интервалов цен.

Решение задачи:

В соответствии с ограничениями и полученными параметрами строим первую симплекс таблицу: В соответствии с ограничениями и полученными параметрами строим первую симплекс таблицу: Решение начинаем при

При решение найдено. Найдем интервал изменения , при котором решение будет оставаться оптимальным. При решение найдено. Найдем интервал изменения , при котором решение будет оставаться оптимальным. При > выбранный столбец является разрешающим. Для нахождения нового оптимального решения при >

Ищем решение при Ищем решение при

Ответ: Ответ: