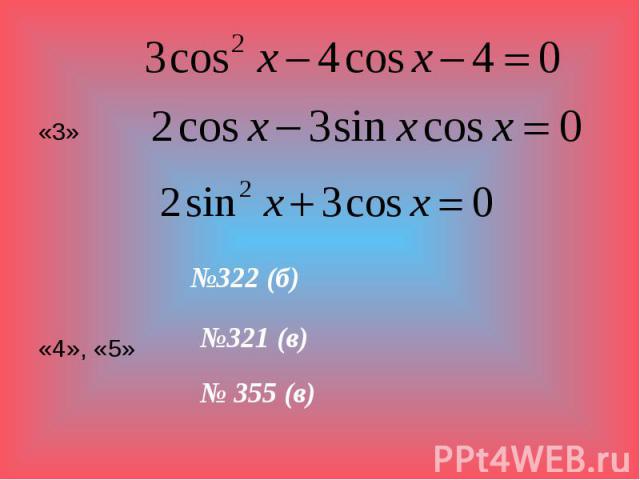Презентация на тему: Тригонометрические уравнения

Анатоль Франс 1844 - 1924

Тригонометрические уравнения вида cost =а, sint =a .

Исторические сведения о развитии тригонометрии.

В школе с тригонометрическим материалом впервые мы знакомимся в курсе планиметрии. С помощью тригонометрии решали плоские треугольники. Тригонометрические соотношения получили названия «синус», «тангенс» и т.д., а их значения были уже вычисленными и сведенными в таблицы. В школе с тригонометрическим материалом впервые мы знакомимся в курсе планиметрии. С помощью тригонометрии решали плоские треугольники. Тригонометрические соотношения получили названия «синус», «тангенс» и т.д., а их значения были уже вычисленными и сведенными в таблицы.

Тригонометрические соотношения определяются теперь с помощью окружности (её обычно называют производящей окружностью), а не прямоугольного треугольника. Хотя они по-прежнему определяются как функции углов, но эти углы уже произвольно велики, их меры выражаются в радианах. Иначе выглядит и тригонометрические тождества, и постановка задач, и трактовка их решений. Вводится графики тригонометрических функций. Наконец, появляются тригонометрические уравнения. И весь этот материал представлен перед нами, учащимися, уже как часть алгебры, а не геометрии, как прежде. Тригонометрические соотношения определяются теперь с помощью окружности (её обычно называют производящей окружностью), а не прямоугольного треугольника. Хотя они по-прежнему определяются как функции углов, но эти углы уже произвольно велики, их меры выражаются в радианах. Иначе выглядит и тригонометрические тождества, и постановка задач, и трактовка их решений. Вводится графики тригонометрических функций. Наконец, появляются тригонометрические уравнения. И весь этот материал представлен перед нами, учащимися, уже как часть алгебры, а не геометрии, как прежде.

Затем тригонометрия появляется в системе начал математического анализа. Здесь речь идет о классе аналитических функций, называемых тригонометрическими, об их структуре, свойствах и приложениях. Их специфические свойства (периодичность, четность или нечетность и др.) позволяют с помощью формул приведения и иных формул тригонометрии и существенно упрощать аналитический аппарат выражений, связанных с этими функциями, и значительно облегчают операцию с ними. Затем тригонометрия появляется в системе начал математического анализа. Здесь речь идет о классе аналитических функций, называемых тригонометрическими, об их структуре, свойствах и приложениях. Их специфические свойства (периодичность, четность или нечетность и др.) позволяют с помощью формул приведения и иных формул тригонометрии и существенно упрощать аналитический аппарат выражений, связанных с этими функциями, и значительно облегчают операцию с ними.

История становления тригонометрии Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.

Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями. Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604. Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Долгое время тригонометрия носила чисто геометрический характер, т. е. факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Долгое время тригонометрия носила чисто геометрический характер, т. е. факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения.

После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще, Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

Синус sin Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия. Современный синус, например, изучался как полухорда, на которую опирается центральный угол, или как хорда удвоенной дуги. В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Отрезок АМ он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна).

y = sin x, D(y) = R, E(y) = [-1;1]

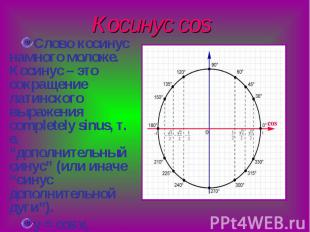
Косинус cos Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”). y = cos x, D (y) = R, E(y) = [-1;1]

Значение обратных тригонометрических функций arccos = arcsin (-1) = arccos 0 = arccos 1 = arccos = arcsin = arcsin =

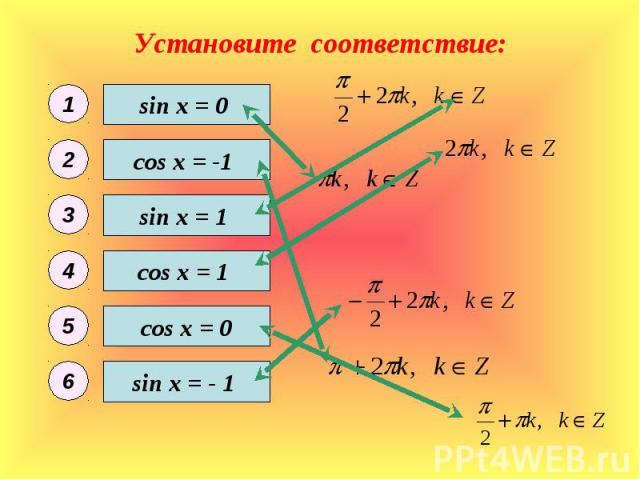
Установите соответствие:

Установите соответствие:

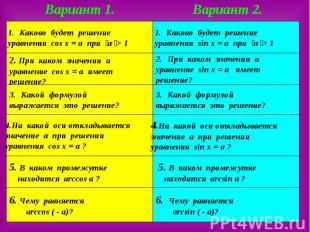
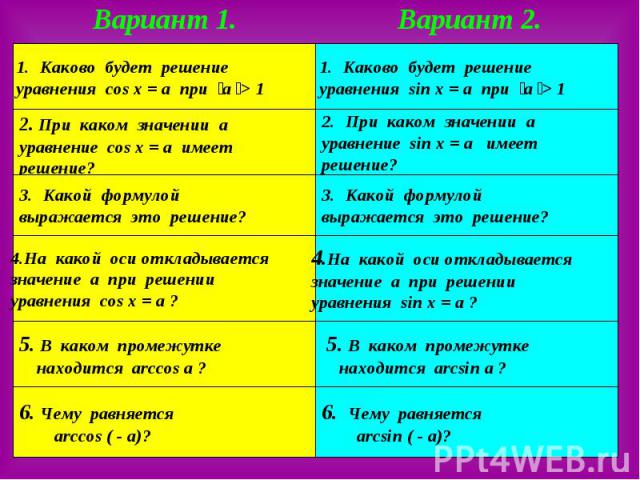
Методы решения тригонометрических уравнений.

Методы решения тригонометрических уравнений.

Методы решения тригонометрических уравнений.

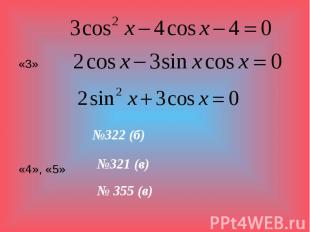
«3» «3» «4», «5»

Домашнее задание: