Презентация на тему: Скалярное произведение

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ Угол между векторами пространстве определяется аналогично тому, как это делалось для векторов на плоскости. А именно, угол между одинаково направленными векторами считается равным нулю. В остальных случаях векторы откладываются от общего начала, и угол между ними определяется как угол между векторами, лежащими в одной плоскости. Скалярное произведение векторов и обозначается По определению, где φ – угол между векторами и . Произведение называется скалярным квадратом и обозначается . Из формулы скалярного произведения следует равенство Скалярным произведением двух ненулевых векторов называется произведение их длин на косинус угла между ними. Если хотя бы один из векторов нулевой, то скалярное произведение таких векторов считается равным нулю. 900igr.net

СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ Для скалярного произведения векторов справедливы свойства, аналогичные свойствам произведения чисел: 1. 2. 3. Используя формулу и формулу скалярного произведения, можно находить угол между векторами. Теорема. Скалярное произведение векторов , выражается формулой
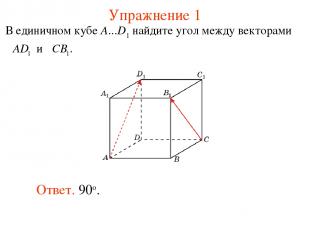
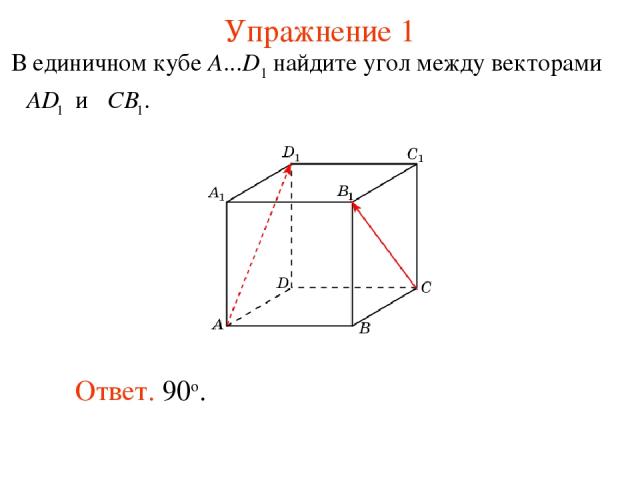
Упражнение 1 Ответ. 90о.
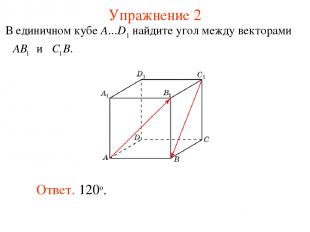
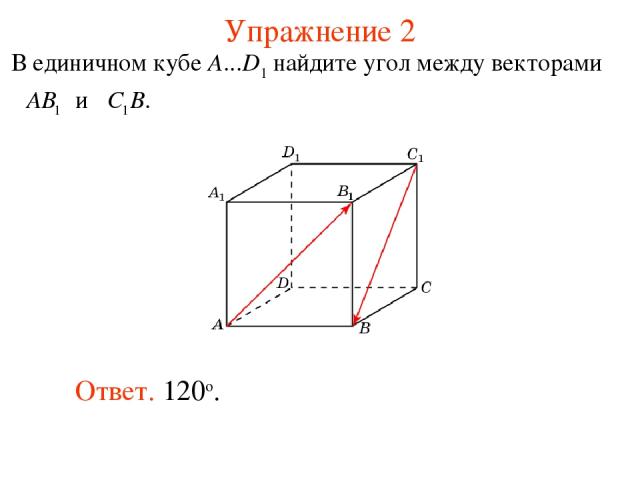
Упражнение 2 Ответ. 120о.
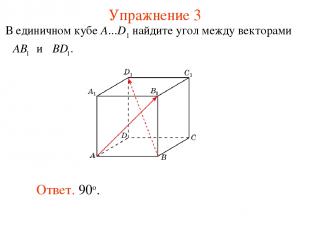
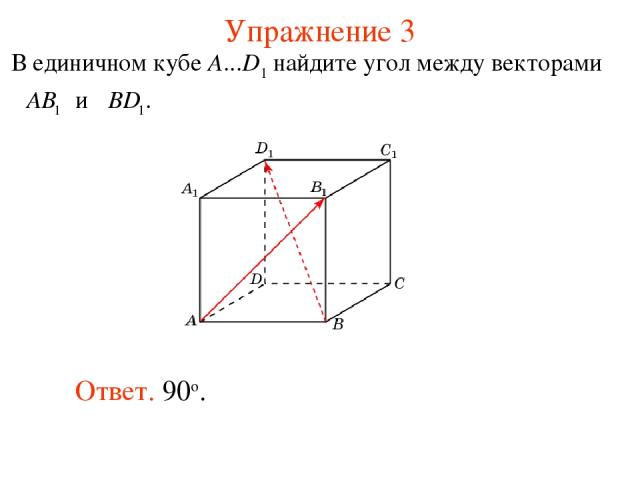
Упражнение 3 Ответ. 90о. В единичном кубе A...D1 найдите угол между векторами и
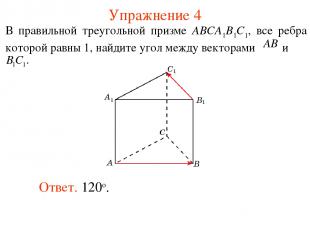
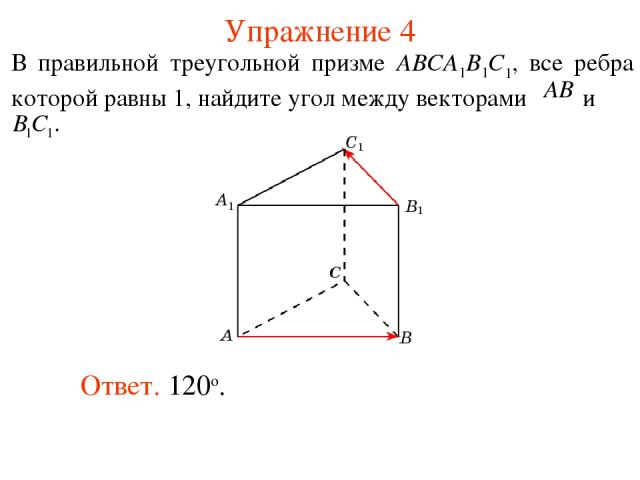
Упражнение 4 Ответ. 120о.

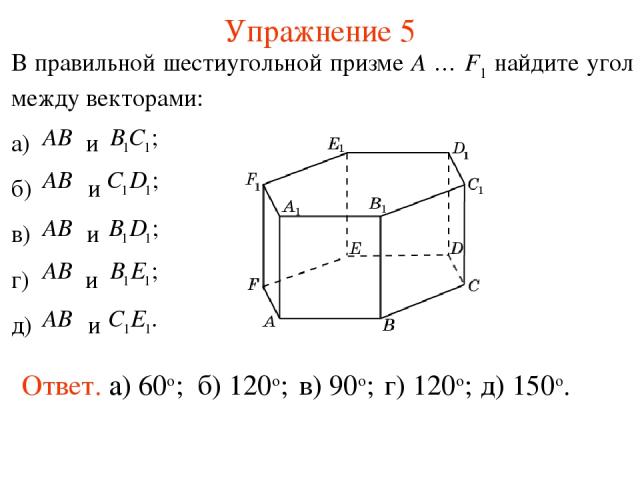
Упражнение 5 Ответ. а) 60о; б) 120о; в) 90о; г) 120о; д) 150о.

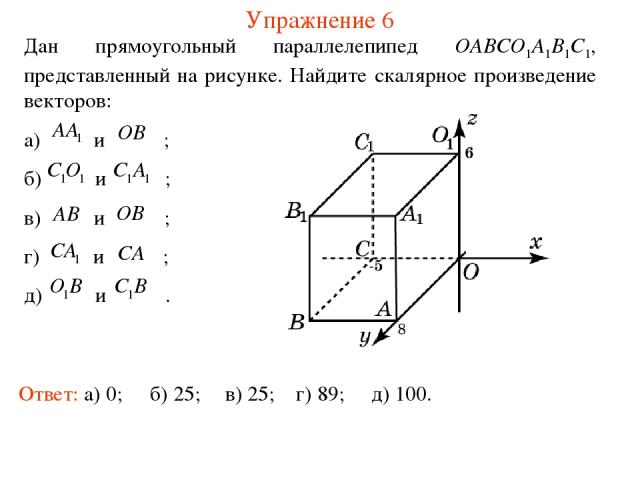
Упражнение 6 Дан прямоугольный параллелепипед OABCO1A1B1C1, представленный на рисунке. Найдите скалярное произведение векторов: а) и ; б) и ; в) и ; г) и ; д) и . Ответ: а) 0; б) 25; в) 25; г) 89; д) 100.

Упражнение 7 Найдите скалярное произведение векторов (-1, 2, 3) и (2, -1, 0). Ответ: –4.

Упражнение 8 Какой знак имеет скалярное произведение векторов, если угол между ними: а) острый; б) тупой? Ответ: а) Плюс; б) минус.

Упражнение 9 В каком случае скалярное произведение двух ненулевых векторов равно нулю? Ответ: Если они перпендикулярны.

Упражнение 10 Найдите угол между векторами: а) (2, 3, -1) и (1, -2, 4); б) (1, 2, -2) и (1, 0, -1). б) = 45о.

Упражнение 11 При каком значении z векторы и перпендикулярны? Ответ: z = -2.

Упражнение 12 Точки M, N, P – середины ребер AB, AD, DC правильного тетраэдра с ребром 4. Найдите скалярные произведения: а) б) в) г) д) е) Ответ: а) 2; б) -2; в) -2; г) 1; д) -1; е) 0.

Упражнение 13 Найдите углы, которые образует с координатными векторами вектор: а) б) в) г) (0, 3, 4). в) 180о, 90о, 90о;

Упражнение 14 Найдите координаты единичного вектора, если известно, что он перпендикулярен векторам с координатами (1,1,0), (0,1,1).