Презентация на тему: Правильная пирамида

Тема урока: «Правильная пирамида».

Цели урока: введение понятия правильной пирамиды;рассмотрение свойств правильной пирамиды;введение понятия апофема;рассмотрение задач на нахождение элементов правильной пирамиды

Ответить на вопросы Сформулируйте определение пирамиды. Покажите на модели (чертеже) ее элементы. Сформулируйте определение высоты пирамиды.Сколько граней, перпендикулярных к плоскости основания, может иметь пирамида?Существует ли четырехугольная пирамида, у которой противоположные боковые грани перпендикулярны к основанию?Могут ли все грани треугольной пирамиды быть прямоугольными треугольниками?Что называется площадью боковой поверхности пирамиды, площадью полной поверхности пирамиды?

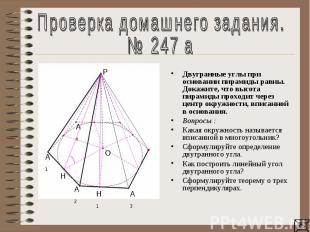
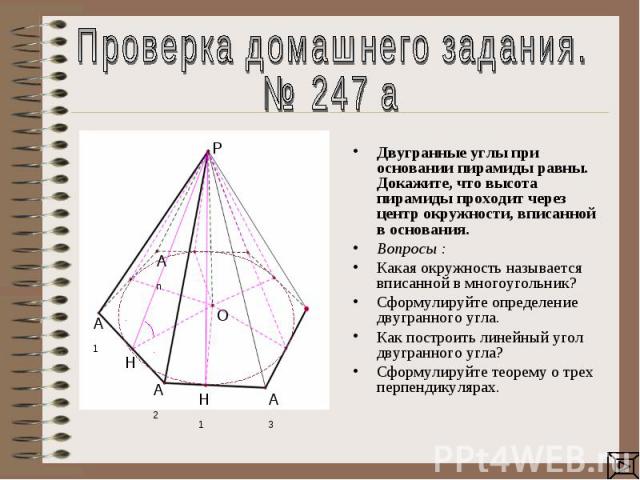
Проверка домашнего задания.№ 247 а Двугранные углы при основании пирамиды равны. Докажите, что высота пирамиды проходит через центр окружности, вписанной в основания. Вопросы : Какая окружность называется вписанной в многоугольник?Сформулируйте определение  двугранного угла.Как построить линейный угол двугранного угла?Сформулируйте теорему о трех перпендикулярах.

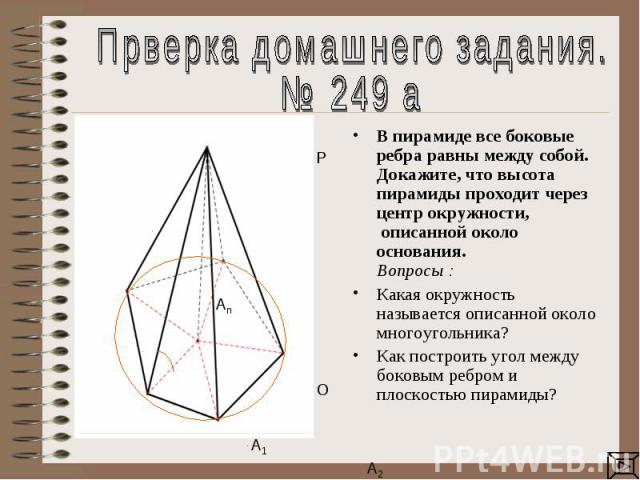
Прверка домашнего задания.№ 249 аВ пирамиде все боковые ребра равны между собой. Докажите, что высота пирамиды проходит через центр окружности,  описанной около основания. Вопросы : Какая окружность называется описанной около многоугольника?Как построить угол между боковым ребром и плоскостью пирамиды?

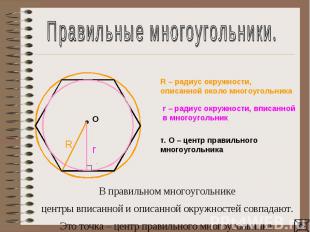
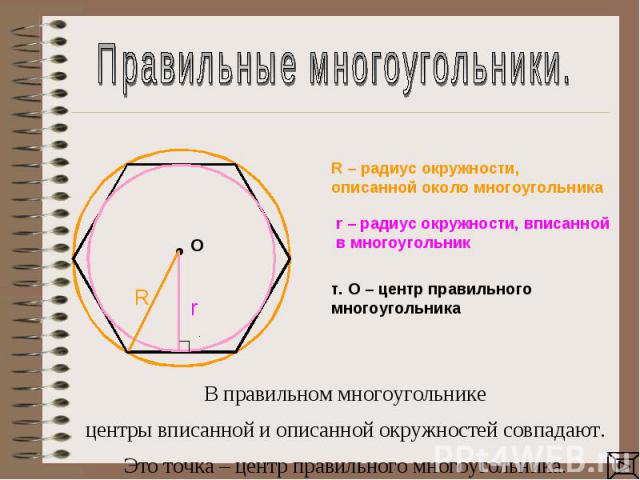
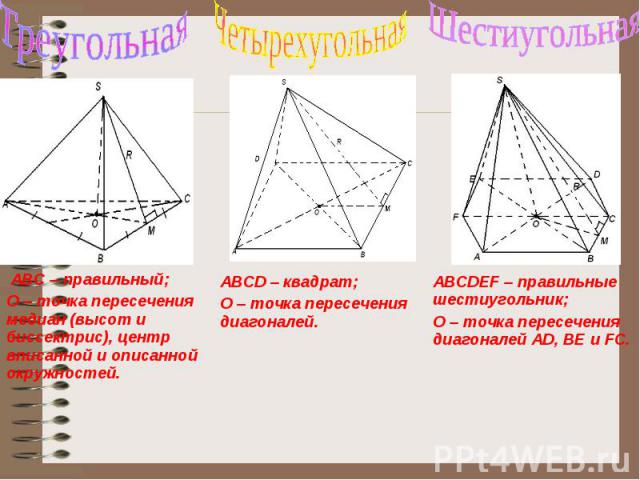
Правильные многоугольники.В правильном многоугольникецентры вписанной и описанной окружностей совпадают. Это точка – центр правильного многоугольника.

Правильные многоугольники.Формулы для вычисления элементов правильного многоугольника:

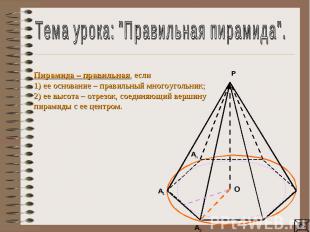
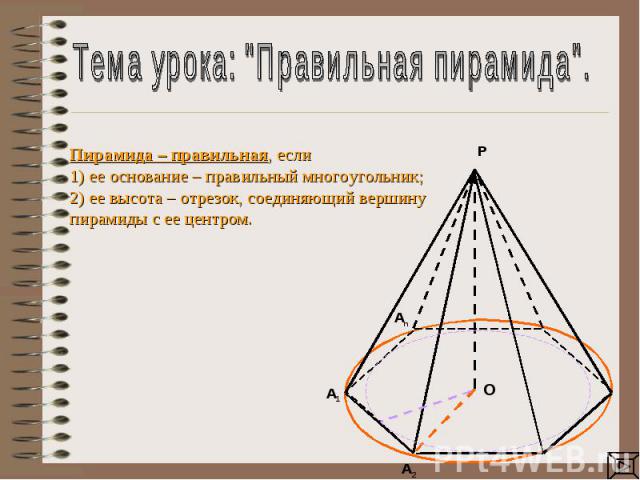
Тема урока: "Правильная пирамида".Пирамида – правильная, если1) ее основание – правильный многоугольник;2) ее высота – отрезок, соединяющий вершину пирамиды с ее центром.

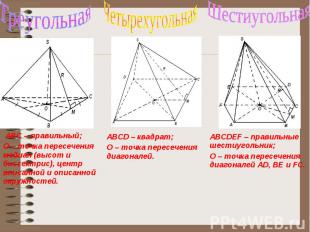
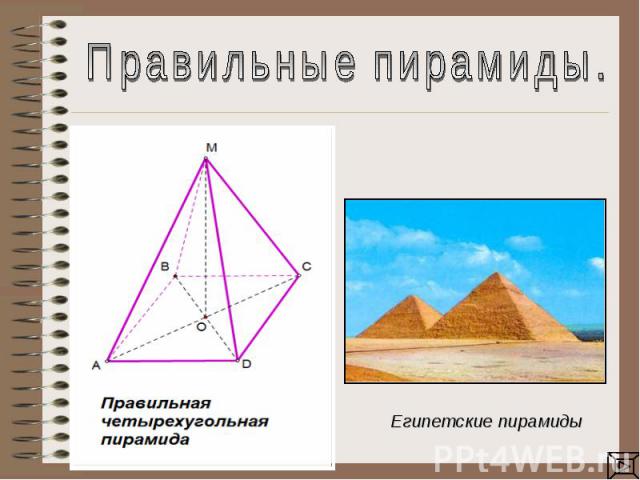
Правильные пирамиды.

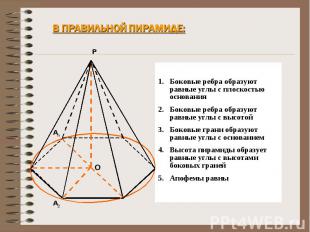
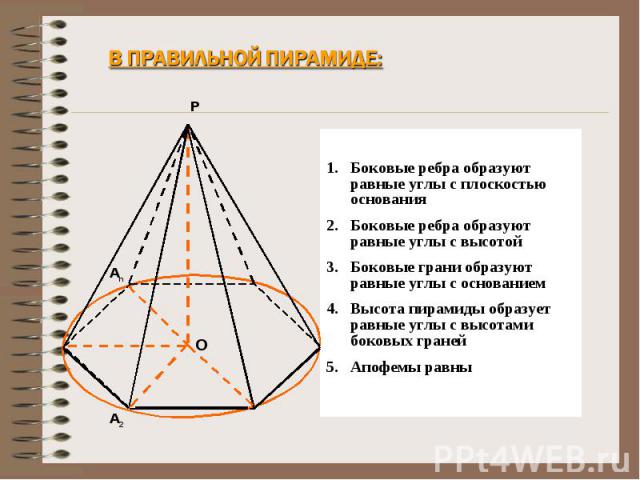
В правильной пирамиде: Боковые ребра образуют равные углы с плоскостью основанияБоковые ребра образуют равные углы с высотойБоковые грани образуют равные углы с основаниемВысота пирамиды образует равные углы с высотами боковых гранейАпофемы равны

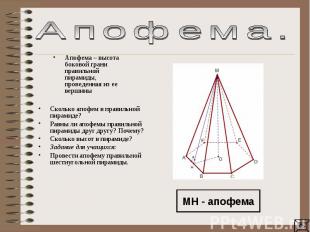
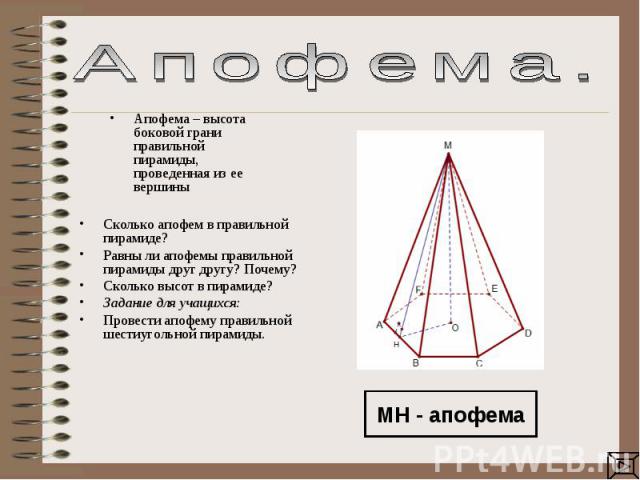
Апофема. Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины Сколько апофем в правильной пирамиде? Равны ли апофемы правильной пирамиды друг другу? Почему?Сколько высот в пирамиде?Задание для учащихся: Провести апофему правильной шестиугольной пирамиды.

Задача. В правильной четырехугольной пирамиде построить:а) угол между боковым ребром и плоскостью основания;б) линейный угол двугранного угла при основании;в) линейный угол двугранного угла между боковыми гранями.

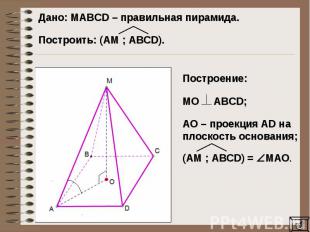
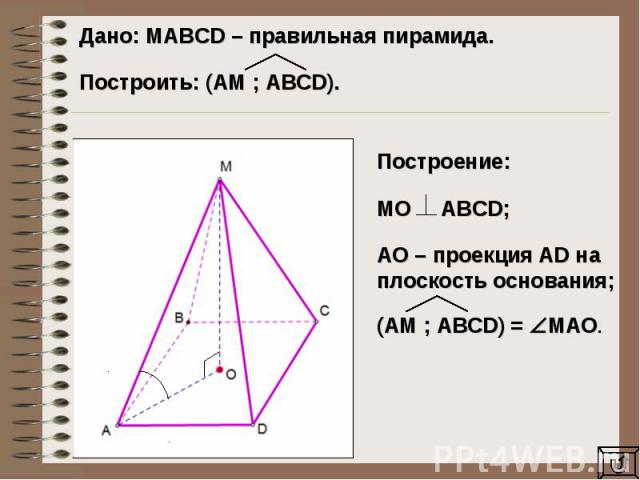
Дано: MAВCD – правильная пирамида. Построить: (AM ; ABCD). Построение: МО ABCD;AO – проекция AD на плоскость основания;(AM ; ABCD) = МAO.

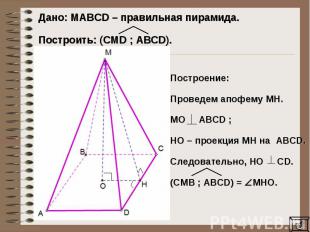
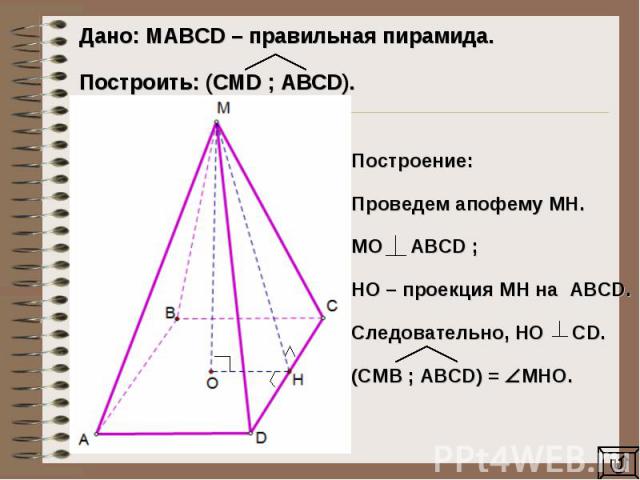
Дано: MAВCD – правильная пирамида. Построить: (CMD ; ABCD).Построение: Проведем апофему МН.МO AВСD ;НО – проекция МН на ABCD.Следовательно, НО CD.(СMВ ; ABCD) = МНО.

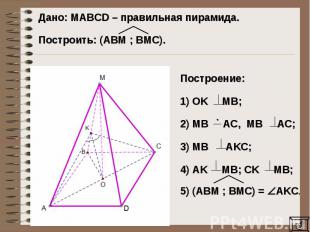
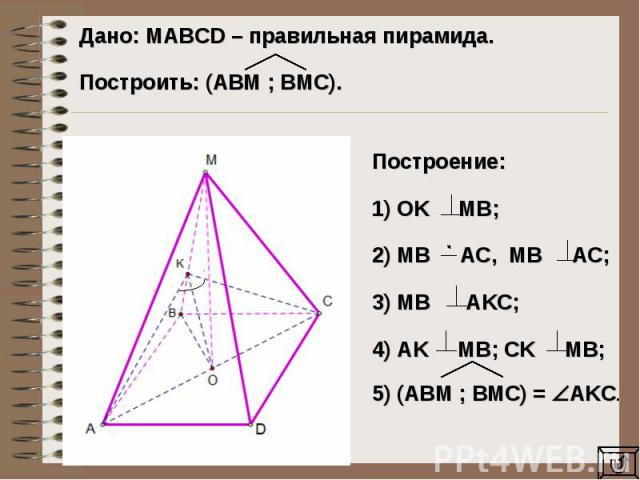
Дано: MAВCD – правильная пирамида. Построить: (AВM ; BМC).Построение: 1) OK MB;2) MB AC, MB AC;3) MB AKC;4) AK MB; CK MB;5) (ABM ; BMC) = AKC.

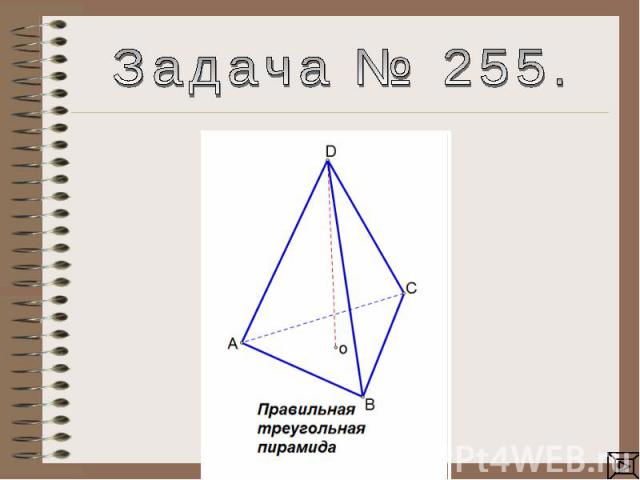
Задача № 255.

Итоги урока.Какая пирамида называется правильной? Являются ли равными боковые ребра правильной пирамиды?Чем являются боковые грани правильной пирамиды?Что называется апофемой?Сколько высот в пирамиде? Сколько апофем в пирамиде?

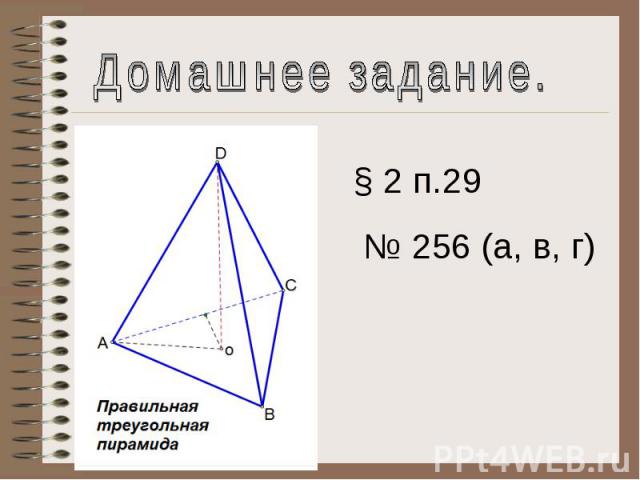
Домашнее задание.§ 2 п.29 № 256 (а, в, г)