Презентация на тему: Пирамида. Построение пирамиды и её плоских сечений. Усечённая пирамида. Правильная пирамида.

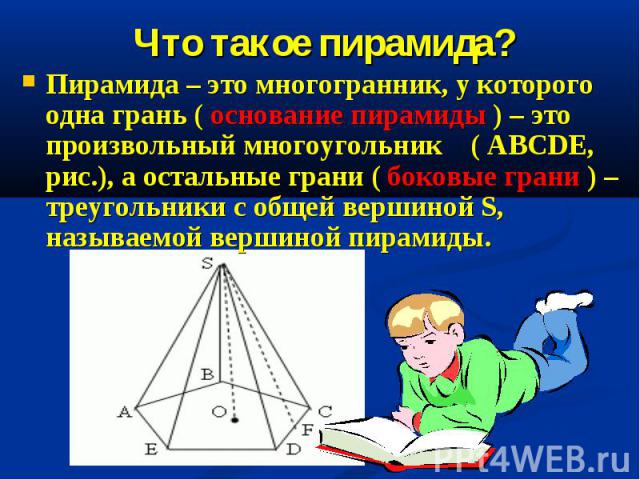
Пирамида – это многогранник, у которого одна грань ( основание пирамиды ) – это произвольный многоугольник ( ABCDE, рис.), а остальные грани ( боковые грани ) – треугольники с общей вершиной S, называемой вершиной пирамиды. Пирамида – это многогранник, у которого одна грань ( основание пирамиды ) – это произвольный многоугольник ( ABCDE, рис.), а остальные грани ( боковые грани ) – треугольники с общей вершиной S, называемой вершиной пирамиды.

Перпендикуляр SO, опущенный из вершины пирамиды на её основание, называется высотой пирамиды. В зависимости от формы многоугольника, лежащего в основании, пирамида может быть соответственно: Перпендикуляр SO, опущенный из вершины пирамиды на её основание, называется высотой пирамиды. В зависимости от формы многоугольника, лежащего в основании, пирамида может быть соответственно:

Пирамида называется правильной, если в основании лежит правильный многоугольник, а её высота падает в центр основания. Все боковые рёбра правильной пирамиды равны; все боковые грани – равнобедренные треугольники. Высота боковой грани (SF) называется апофемой правильной пирамиды. Пирамида называется правильной, если в основании лежит правильный многоугольник, а её высота падает в центр основания. Все боковые рёбра правильной пирамиды равны; все боковые грани – равнобедренные треугольники. Высота боковой грани (SF) называется апофемой правильной пирамиды.

Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.

Если сторона основания a, число сторон n, то боковая поверхность пирамиды равна: Если сторона основания a, число сторон n, то боковая поверхность пирамиды равна: где l - апофема, а p - периметр основания пирамиды.Теорема доказана.

Если провести сечение abcde, параллельное основанию ABCDE ( рис. ) пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани ABCDE и abcde называются основаниями; расстояние Oo между ними – высотой. Если провести сечение abcde, параллельное основанию ABCDE ( рис. ) пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани ABCDE и abcde называются основаниями; расстояние Oo между ними – высотой.