Презентация на тему: Вероятность и геометрия

Для нахождения вероятности случайного события A при проведении некоторого числа опытов следует: Для нахождения вероятности случайного события A при проведении некоторого числа опытов следует: Найти число N всех возможных исходов данного испытания; Найти количество N(A) тех исходов опыта, в которых наступает событие A; Найти частное N(A)/N; оно и будет равно вероятности события A.

Вероятностью события A при проведении некоторого испытания называют отношение числа тех исходов, в результате которых наступает событие A, к общему числу всех (равновозможных между собой) исходов этого испытания. Вероятностью события A при проведении некоторого испытания называют отношение числа тех исходов, в результате которых наступает событие A, к общему числу всех (равновозможных между собой) исходов этого испытания.

Если площадь S(A) фигуры A разделить на площадь S(X) фигуры X, которая целиком содержит фигуру A, то получится вероятность того, что случайно выбранная точка фигуры X окажется в фигуре A: Если площадь S(A) фигуры A разделить на площадь S(X) фигуры X, которая целиком содержит фигуру A, то получится вероятность того, что случайно выбранная точка фигуры X окажется в фигуре A: P=S(A)/S(X)

Отрезок единичной длины случайным образом разделяют на три отрезка. Какова вероятность того, что из них можно сложить треугольник? Отрезок единичной длины случайным образом разделяют на три отрезка. Какова вероятность того, что из них можно сложить треугольник?

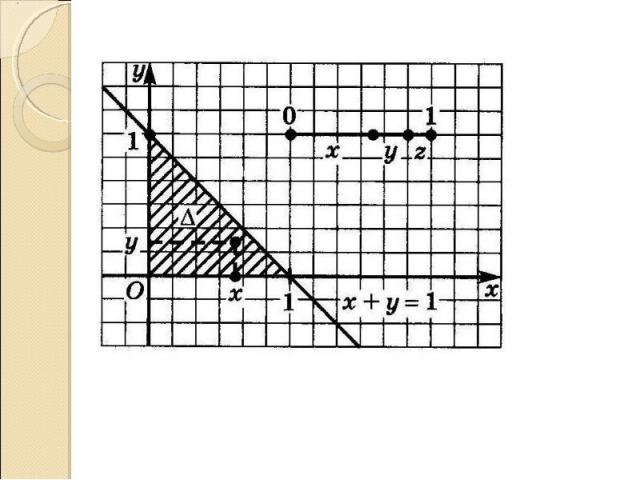
Пронумеруем отрезки слева направо и обозначим их длины за x, y и z. Так как x+y+z=1, то z=1-x-y>0. Значит, x>0, y>0 и при этом x+y<1. В координатной плоскости изобразим множество решений системы трех неравенств: Пронумеруем отрезки слева направо и обозначим их длины за x, y и z. Так как x+y+z=1, то z=1-x-y>0. Значит, x>0, y>0 и при этом x+y<1. В координатной плоскости изобразим множество решений системы трех неравенств: x>0 y>0 x+y<1

Получим треугольник с вершинами (0;0) (1;0) (0;1) без учета его сторон. Каждому способу деления заданного отрезка на три части x,y,z поставим в соответствие точку (x,y) из треугольника. Выбрав точку(x,y) мы однозначно зададим и разбиение заданного отрезка единичной длины на три отрезка [0;x] [x;x+y] [x+y;1]. Получим треугольник с вершинами (0;0) (1;0) (0;1) без учета его сторон. Каждому способу деления заданного отрезка на три части x,y,z поставим в соответствие точку (x,y) из треугольника. Выбрав точку(x,y) мы однозначно зададим и разбиение заданного отрезка единичной длины на три отрезка [0;x] [x;x+y] [x+y;1].

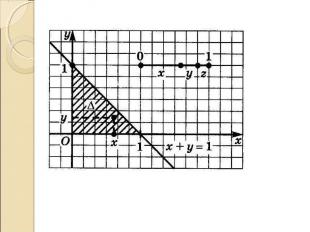
x+y>z x+y>1-x-y x+y>0.5 x+y>z x+y>1-x-y x+y>0.5 x+z>y x+1-x-y>y y<0.5 y+z>x y+1-x-y>x x<0.5 Получаем треугольник, подобный первому с коэффициентом подобия 0,5 S1/S2=1/4

Вероятность того, что точка окажется окажется в меньшем треугольнике P(A)=0.25 Вероятность того, что точка окажется окажется в меньшем треугольнике P(A)=0.25

Случайным образом нарисовали треугольник. Какова вероятность того, что он является остроугольным? Случайным образом нарисовали треугольник. Какова вероятность того, что он является остроугольным?

Переформулируем задачу: Переформулируем задачу: Число 180 случайным образом представили в виде суммы трех положительных слагаемых. Какова вероятность того, что все слагаемые меньше 90?

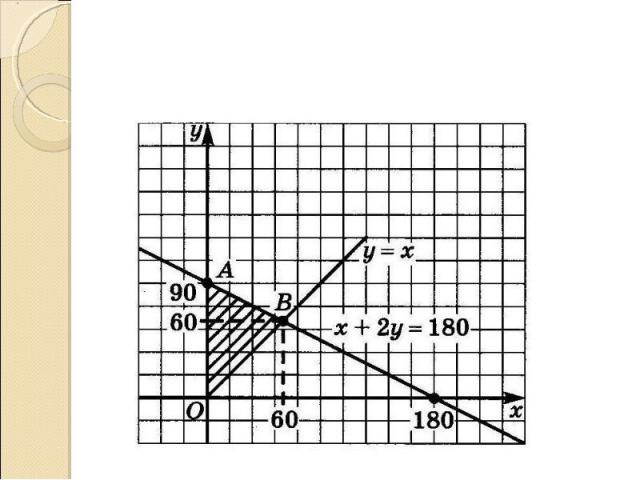
Пусть 0<x<y x+y+z=180 z=180-x-y Пусть 0<x<y x+y+z=180 z=180-x-y 0<x 0<x x<y x<y y<180-x-y x+2y<180 Получим треугольник с вершинами О(0;0) А(0;90) В(60;60). Каждая точка однозначно «отвечает» за треугольник с углами x, y, 180-x-y.

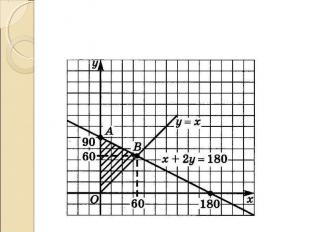
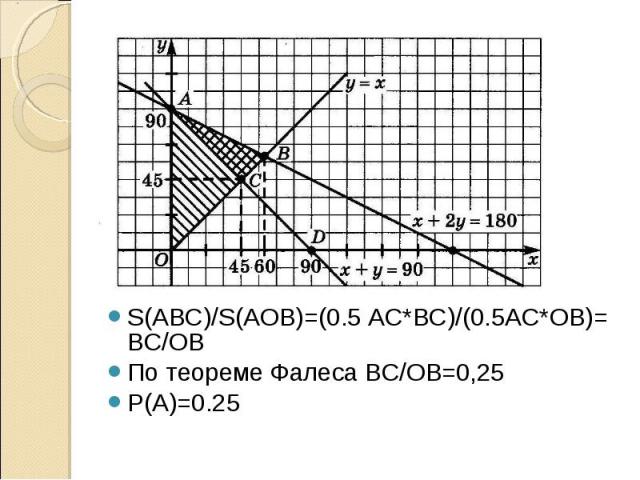
Отметим в нашей модели точки, соответствующие остроугольным треугольникам. Отметим в нашей модели точки, соответствующие остроугольным треугольникам. x<y<90 x<y<90 y<180-x-y<90 x+2y<90 x+y>90 Получаем треугольник с вершинами А(0;90) В(60;60) С(45;45)

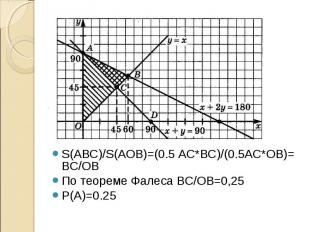
S(ABC)/S(AOB)=(0.5 AC*BC)/(0.5AC*OB)= BC/OB S(ABC)/S(AOB)=(0.5 AC*BC)/(0.5AC*OB)= BC/OB По теореме Фалеса BC/OB=0,25 P(A)=0.25

Два шпиона решили встретиться у фонтана. Каждый из них может гарантировать только то, что он появится у фонтана с 12-00 до 13-00. По инструкции шпион после прихода ждет встречи у фонтана 15 минут и по их истечении (или ровно в 13:00) уходит. Какова вероятность встречи? Два шпиона решили встретиться у фонтана. Каждый из них может гарантировать только то, что он появится у фонтана с 12-00 до 13-00. По инструкции шпион после прихода ждет встречи у фонтана 15 минут и по их истечении (или ровно в 13:00) уходит. Какова вероятность встречи?

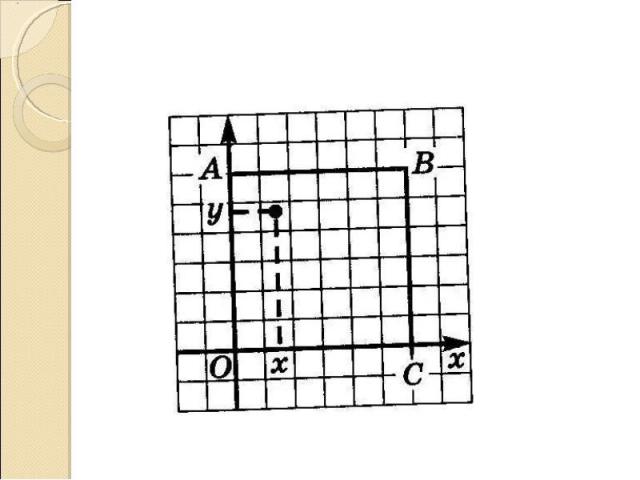
За единицу отсчета возьмем 1 час, а за начало отсчета возьмем 12:00. Пусть x - время прихода первого шпиона, а y - время прихода второго. Тогда o≤x≤1, 0 ≤y ≤1 и точка (x,y) квадрата с вершинами О(0;0) А(0;1) В(1;1) С(1;0) будет соответствовать времени прихода первого и второго шпионов. За единицу отсчета возьмем 1 час, а за начало отсчета возьмем 12:00. Пусть x - время прихода первого шпиона, а y - время прихода второго. Тогда o≤x≤1, 0 ≤y ≤1 и точка (x,y) квадрата с вершинами О(0;0) А(0;1) В(1;1) С(1;0) будет соответствовать времени прихода первого и второго шпионов.

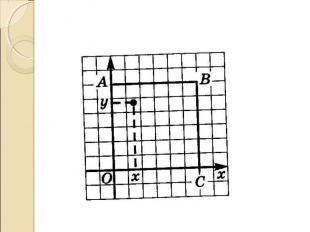
Встреча произойдет, только если время прихода первого шпиона отличается от времени прихода второго не более чем на 15 минут. Т.е. Встреча произойдет, только если время прихода первого шпиона отличается от времени прихода второго не более чем на 15 минут. Т.е. 0 ≤x ≤1 0 ≤x ≤1 0 ≤y ≤1 0 ≤y ≤1 |y-x| ≤0.25 x-0.25 ≤y ≤x+0.25 Получается часть квадрата ОАВС, лежащая между прямыми y=x-0.25 и y=x+0.25

Незаштрихованная часть состоит из двух прямоугольных треугольников, катеты которых равны 0,75. Значит их площадь равна 0,5625. Т.е. заштрихованная часть составляет 0,4375 от площади всего квадрата. Это и есть искомая вероятность P(A)=0.4375 Незаштрихованная часть состоит из двух прямоугольных треугольников, катеты которых равны 0,75. Значит их площадь равна 0,5625. Т.е. заштрихованная часть составляет 0,4375 от площади всего квадрата. Это и есть искомая вероятность P(A)=0.4375

Презентацию выполнила: Презентацию выполнила: Горбунова Елена, ученица 11Б класса, МОУ «Гимназия №11»