Презентация на тему: История тригонометрии


Определения Определения История Синус, косинус, тангенс Дальнейшее развитие Аналитическая теория Список литературы

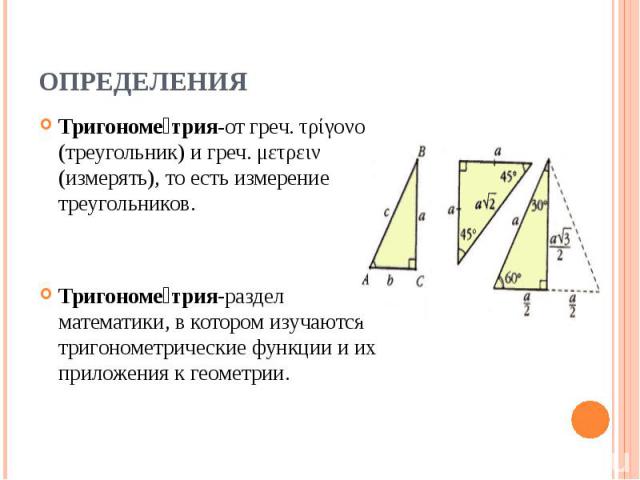
Тригономе трия-от греч. τρίγονο (треугольник) и греч. μετρειν (измерять), то есть измерение треугольников. Тригономе трия-от греч. τρίγονο (треугольник) и греч. μετρειν (измерять), то есть измерение треугольников. Тригономе трия-раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.

Тригонометрия возникла из практических нужд человека. С ее помощью можно определить расстояние до недоступных предметов и, вообще существенно упрощать процесс геодезической съемки местности для составления географических карт. Тригонометрия возникла из практических нужд человека. С ее помощью можно определить расстояние до недоступных предметов и, вообще существенно упрощать процесс геодезической съемки местности для составления географических карт. Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.

Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме. Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме.

Другие источники сообщают, что именно замена хорд синусами стала главным достижением Средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах. Другие источники сообщают, что именно замена хорд синусами стала главным достижением Средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах. Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются так: sin2α + cos2α = 1

Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности встречаются уже в III веке до н.э. в работах великих математиков Древней Греции Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия. Современный синус , например, изучался как полухорда, на которую опирается центральный угол величиной , или как хорда удвоенной дуги. Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности встречаются уже в III веке до н.э. в работах великих математиков Древней Греции Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия. Современный синус , например, изучался как полухорда, на которую опирается центральный угол величиной , или как хорда удвоенной дуги.

Слово косинус намного моложе. Косинус это сокращение латинского выражения completely sinus, т. е. “дополнительный синус”. Слово косинус намного моложе. Косинус это сокращение латинского выражения completely sinus, т. е. “дополнительный синус”. Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов.

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным. Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения.

http://www.shkola.lv/index.php?mode=learn&page=refs&ref_id=14 http://www.shkola.lv/index.php?mode=learn&page=refs&ref_id=14 http://ru.wikipedia.org/wiki/Тригонометрия