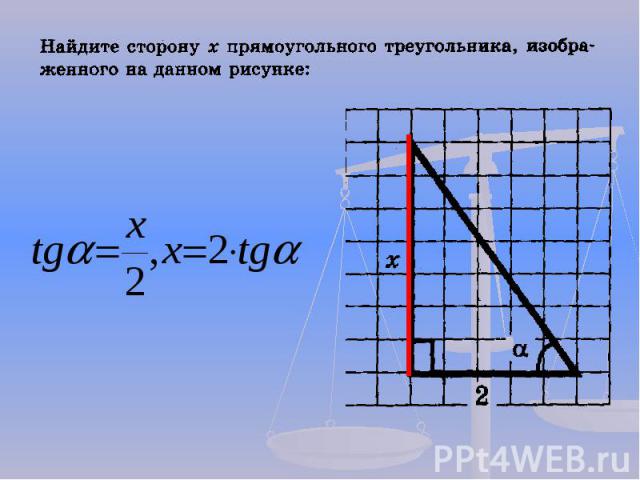
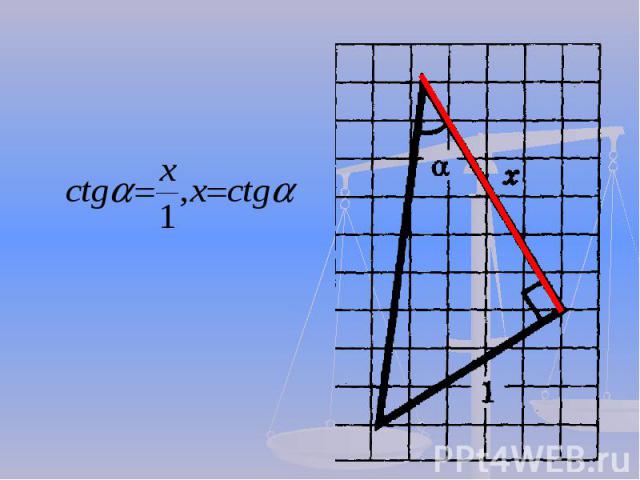
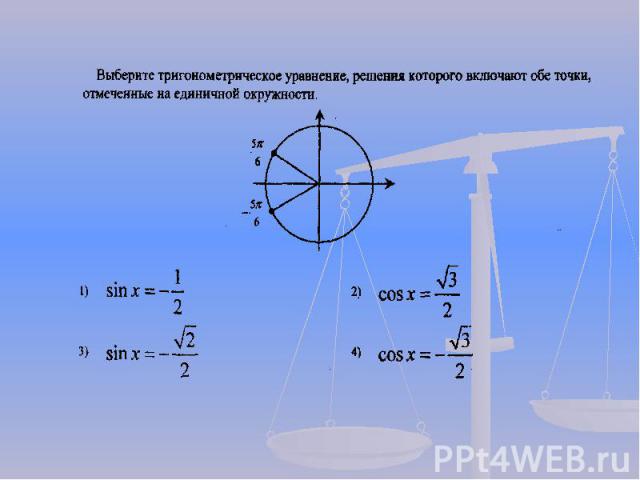
Презентация на тему: Решение задач по механике с использованием тригонометрии

Решение задач по механике с использованием тригонометрии Для профильного физико- математического 10 класса МОУ СОШ 34 Пихтовникова С.А., учитель математики, Бурлаков А.Д., учитель физики.

Наука начинается тогда, когда начинают считать. Д.И.Менделеев

Слеп физик без математики. М.В.Ломоносов

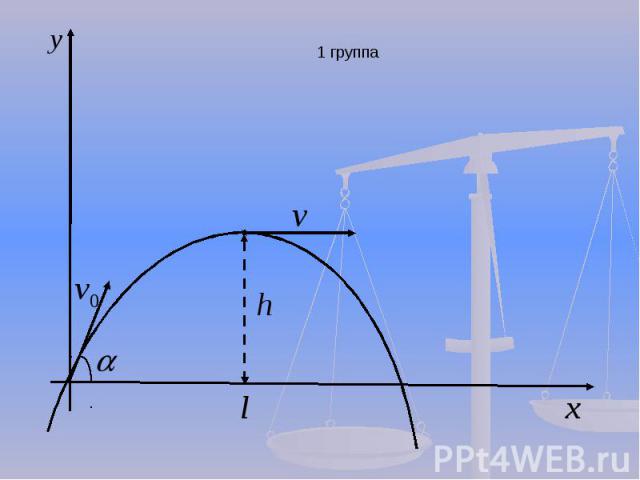
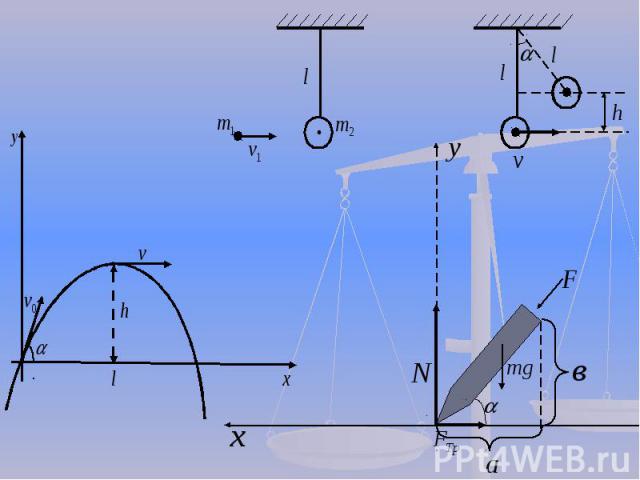
Устно: Уравнение скорости: Уравнение скорости: Перемещение при равноускоренном движении: Перемещение при равноускоренном движении: Тело брошено под углом к горизонту. Дальность полета, высота полета: Тело брошено под углом к горизонту. Дальность полета, высота полета:(дальность)(высота)

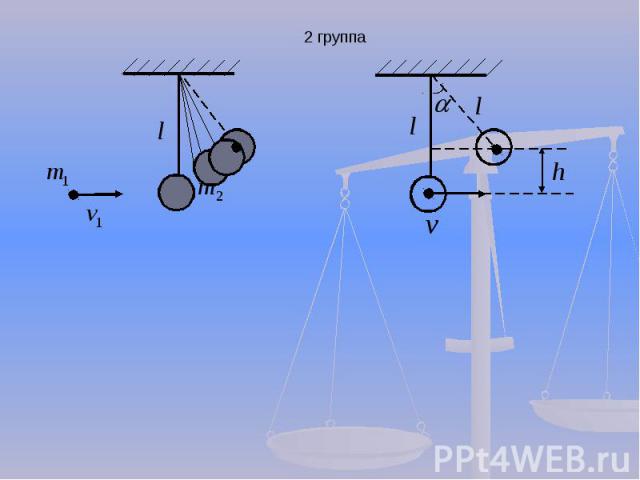
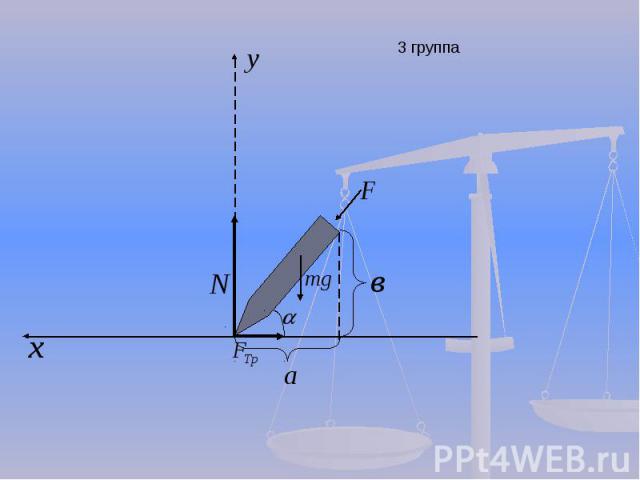
Формула для нахождения силы трения: Формула для нахождения силы трения: Закон сохранения импульса: Закон сохранения импульса: Закон сохранения механической энергии(без учета трения) Закон сохранения механической энергии(без учета трения)

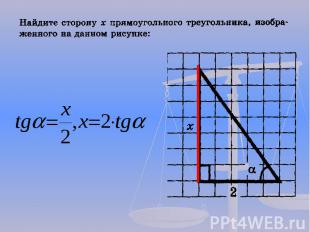
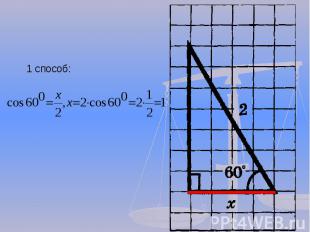
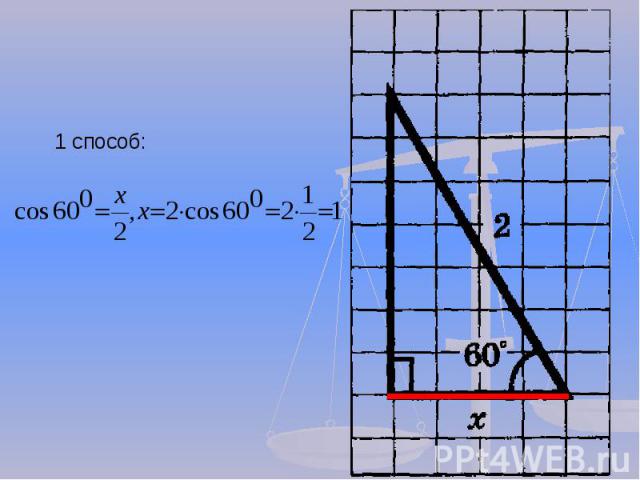
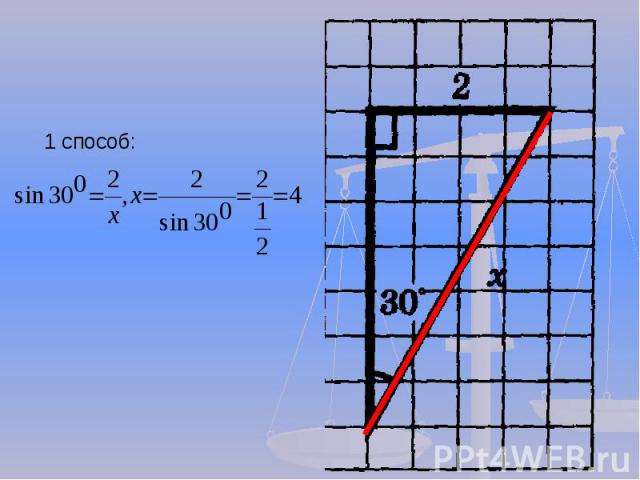
1 способ:

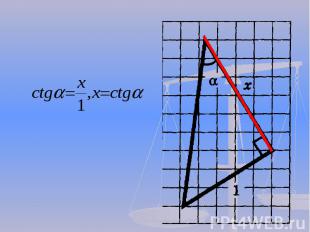
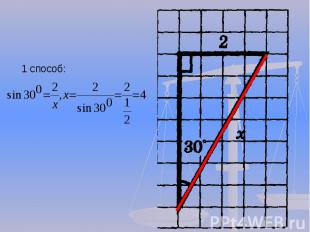
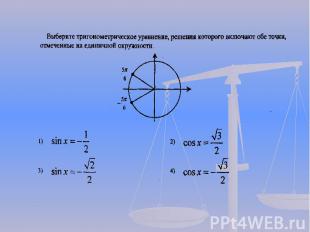
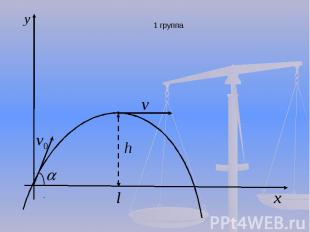
1 группа

2 группа

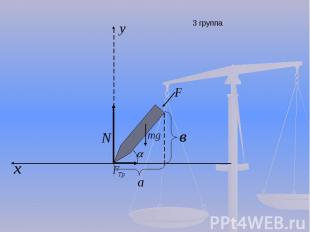
3 группа

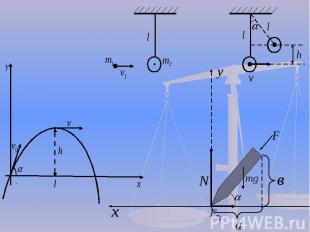
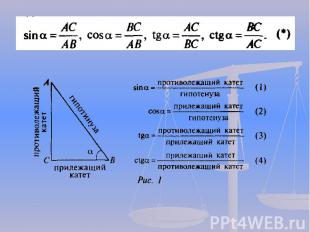
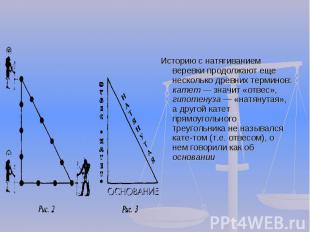
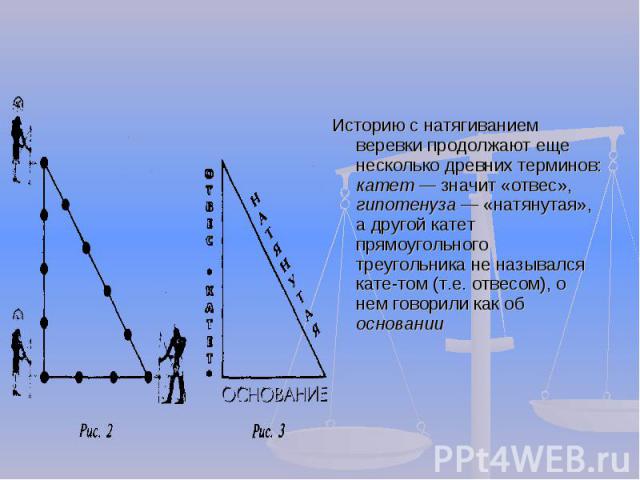
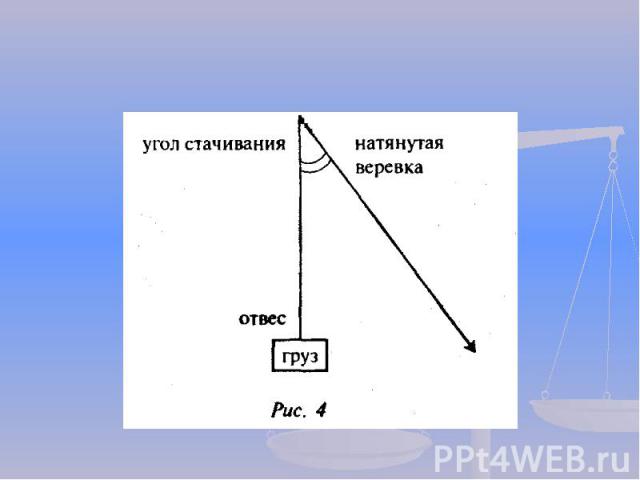
Историю с натягиванием веревки продолжают еще несколько древних терминов: катет значит «отвес», гипотенуза «натянутая», а другой катет прямоугольного треугольника не назывался катетом (т.е. отвесом), о нем говорили как об основании

Задача 1. Определить расстояние от корабля, находящегося в море, до берега

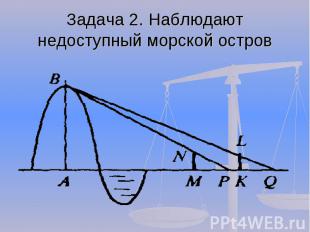
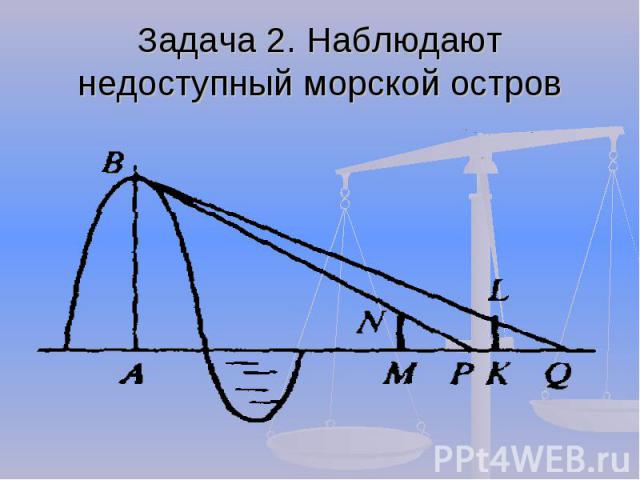
Задача 2. Наблюдают недоступный морской остров

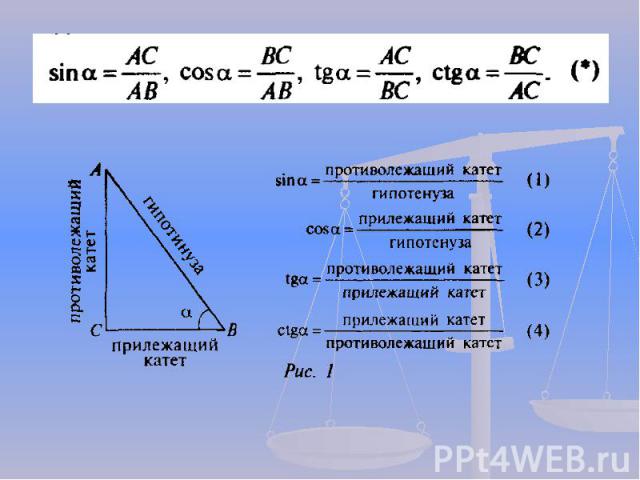
«Тригонометрия», которое буквально означает «измерение треугольника». Термин тригонометрия состоит из двух греческих слов: тригоном, что означает «треугольник» и метрейн, что означает «измерять».

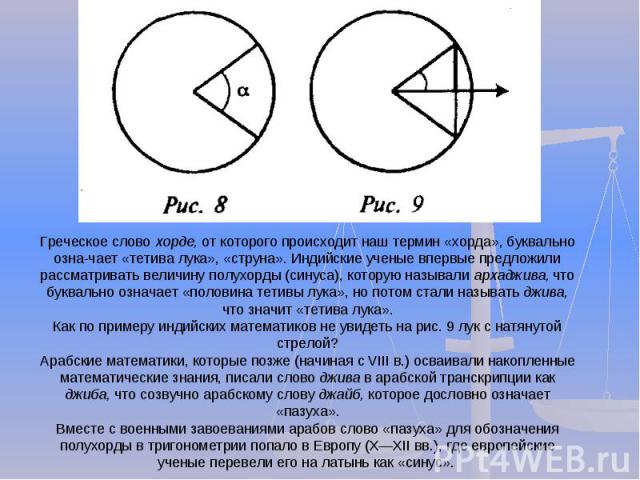
Греческое слово хорде, от которого происходит наш термин «хорда», буквально означает «тетива лука», «струна». Индийские ученые впервые предложили рассматривать величину полухорды (синуса), которую называли архаджива, что буквально означает «половина тетивы лука», но потом стали называть джива, что значит «тетива лука». Как по примеру индийских математиков не увидеть на рис. 9 лук с натянутой стрелой? Арабские математики, которые позже (начиная с VIII в.) осваивали накопленные математические знания, писали слово джива в арабской транскрипции как джиба, что созвучно арабскому слову джайб, которое дословно означает «пазуха». Вместе с военными завоеваниями арабов слово «пазуха» для обозначения полухорды в тригонометрии попало в Европу (XXII вв.), где европейские ученые перевели его на латынь как «синус».

Европейские математики XIIXVI вв. часто называли синус sinus rectus (прямой синус), а радиус тригонометрической окружности sinus totus, т.е. весь (полный) синус. Слово «косинус» это сокращение латинского выражения complementy sinus, т.е. «дополнительный синус» или, иначе, «синус дополнительной дуги»; вспомните: cos a = sin (90° - а).

Начиная с XIVXV вв. центр математических исследований перемещается в Европу. В XIII XIV вв. при переводе арабских произведений на латинский язык новые тригонометрические функции котангенс и тангенс были названы umbra recta -прямая тень, и umbra versa обратная тень. Известно, что линию тангенсов уже использовал в своих работах английский математик Томас Брадвар-дин (1290-1349). Начиная с XIVXV вв. центр математических исследований перемещается в Европу. В XIII XIV вв. при переводе арабских произведений на латинский язык новые тригонометрические функции котангенс и тангенс были названы umbra recta -прямая тень, и umbra versa обратная тень. Известно, что линию тангенсов уже использовал в своих работах английский математик Томас Брадвар-дин (1290-1349). Термин tangens (от лат. касающийся [отрезок касательной]) был введен только в 1583 г. датским математиком Томасом Финком в связи с ролью этой линии на тригонометрической окружности. Термин «котангенс» образован по аналогии с термином «косинус», и встречается впервые в 1620 г. у английского ученого Эдмунта Гутера. Термин tangens (от лат. касающийся [отрезок касательной]) был введен только в 1583 г. датским математиком Томасом Финком в связи с ролью этой линии на тригонометрической окружности. Термин «котангенс» образован по аналогии с термином «косинус», и встречается впервые в 1620 г. у английского ученого Эдмунта Гутера.

Если до этого главной целью тригонометрии считалось решение треугольников, вычисление элементов геометрических фигур, а учение о тригонометрических функциях строилось на геометрической основе, то развитие нового (аналитического) направления привело к тому, что тригонометрия постепенно стала одной из глав математического анализа. Начало этого преображения тригонометрии связано с именем знаменитого ученого много лет работавшего в Петербурге Леонарда Эйлера (17071783). Эйлер усовершенствовал как символику, так и содержание тригонометрии.

Практическая работа: