Презентация на тему: Параллельные прямые

ТЕМА: Параллельные прямые ТЕМА: Параллельные прямые

Дайте определение параллельных прямых. Дайте определение параллельных прямых. Что такое секущая? Назовите углы при пересечении двух прямых секущей. Перечислите признаки параллельности прямых. Что такое аксиома параллельности?

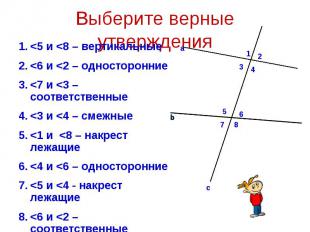
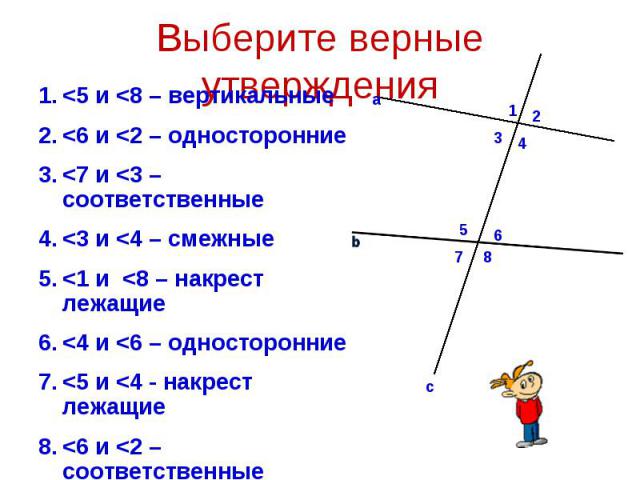
<5 и <8 – вертикальные <5 и <8 – вертикальные <6 и <2 – односторонние <7 и <3 – соответственные <3 и <4 – смежные <1 и <8 – накрест лежащие <4 и <6 – односторонние <5 и <4 - накрест лежащие <6 и <2 – соответственные <2 и <7 - вертикальные

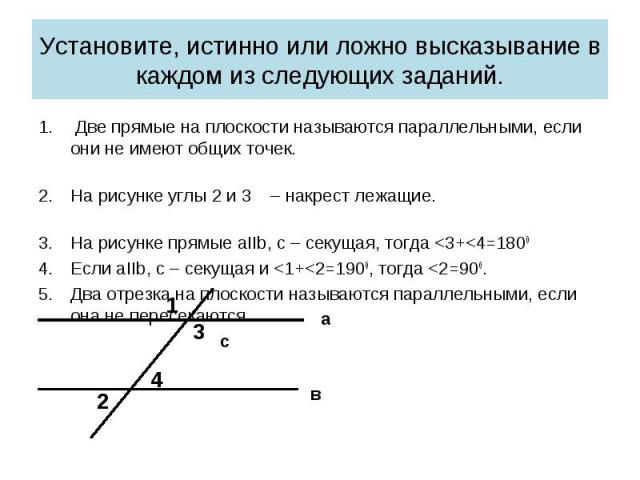
Две прямые на плоскости называются параллельными, если они не имеют общих точек. Две прямые на плоскости называются параллельными, если они не имеют общих точек. На рисунке углы 2 и 3 – накрест лежащие. На рисунке прямые aΙΙb, c – секущая, тогда <3+<4=1800 Если aΙΙb, c – секущая и <1+<2=1900, тогда <2=900. Два отрезка на плоскости называются параллельными, если она не пересекаются. c

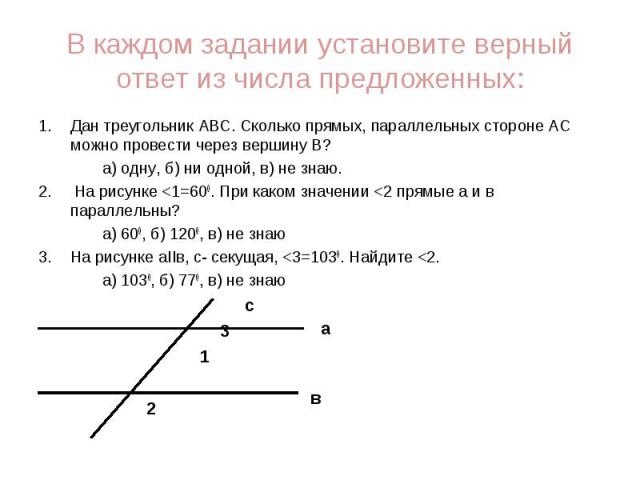
Дан треугольник АВС. Сколько прямых, параллельных стороне АС можно провести через вершину В? Дан треугольник АВС. Сколько прямых, параллельных стороне АС можно провести через вершину В? а) одну, б) ни одной, в) не знаю. 2. На рисунке <1=600. При каком значении <2 прямые а и в параллельны? а) 600, б) 1200, в) не знаю На рисунке аIIв, с- секущая, <3=1030. Найдите <2. а) 1030, б) 770, в) не знаю с 3 1 2

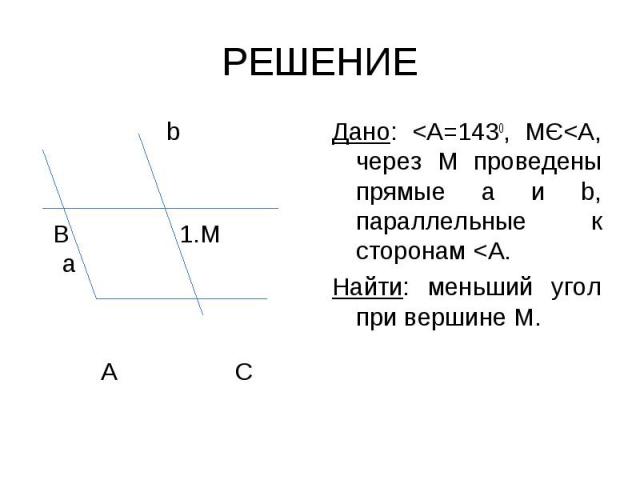
Из произвольной точки М, взятой внутри угла А, который равен 1430, проведены прямые, параллельные сторонам угла А. Найдите величину меньшего из углов, образовавшихся при вершине М. Из произвольной точки М, взятой внутри угла А, который равен 1430, проведены прямые, параллельные сторонам угла А. Найдите величину меньшего из углов, образовавшихся при вершине М. Варианты ответа: а) 370, б) 1430, в) не знаю Смотри решение

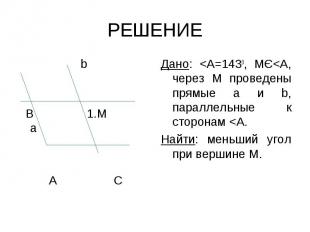
b b В 1.М а А С

1. По условию прямые аIIАС при секущей АВ. 1. По условию прямые аIIАС при секущей АВ. Т. К. <А=1430, то по 3 свойству параллельных прямых <А+<АВМ=1800 – односторонние, следовательно <АМВ=1800-1430=370 2. По условию прямые bIIАВ при секущей а. <АМВ=<1, как накрест лежащие углы по первому свойству параллельности, следовательно <1=370. ОТВЕТ: <1=370.