Презентация на тему: Объем прямоугольного параллелепипеда

Тема урока: Тема урока: Объем прямоугольного параллелепипеда

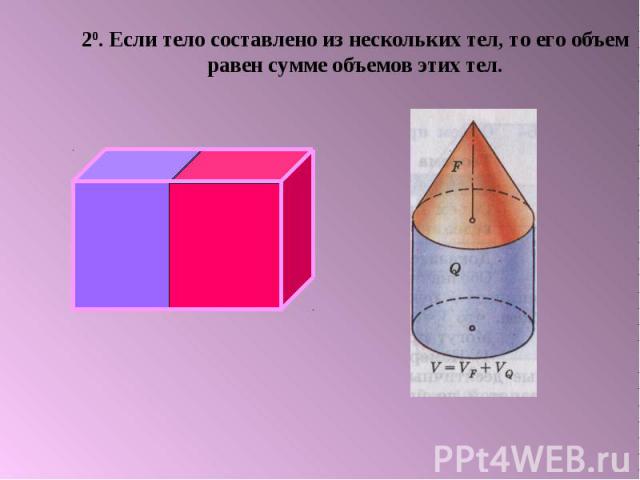
Величина части пространства, занимаемого геометрическим телом , называется объемом этого тела

Английские меры объема Бушель - 36,4 дм3 Галлон -4,5 дм3 Баррель (сухой)- 115,628 дм3 Баррель (нефтяной)- 158,988 дм3 Английский баррель для сыпучих веществ 163,65 дм3

Ведро - 12 дм3 Бочка - 490 дм3 Штоф - 1,23 дм3 = 10 чарок Чарка -0,123 дм3=0,1 штофа= = 2 шкалика Шкалик -0,06 дм 3 = 0,5 чарки

На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с вписанным шаром, а эпитафия говорила о величайшем открытии Архимеда - о том, что объемы этих тел относятся как 3: 2. На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с вписанным шаром, а эпитафия говорила о величайшем открытии Архимеда - о том, что объемы этих тел относятся как 3: 2. Когда Римский оратор и общественный деятель Цицерон, живший в 1 в. до н.э., был в Сицилии, он еще видел этот заросший кустами и терновником памятник с шаром и цилиндром.

Понятие объема За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называют кубическим сантиметром и обозначают см3.

Два тела называют равными, если их можно совместить наложением. Два тела называют равными, если их можно совместить наложением.

Объем прямоугольного параллелепипеда. Теорема. Объем прямоугольного параллелепипеда равен произведению трех его измерений. Дано: параллелепипед, а, b, c его измерения.V - объем Доказать: V = abc. Доказательство: 1 сл. Пусть а, b, c - конечные десятичные дроби ( n 1) . Числа а ·10n , b ·10 n, c·10 n - целые . Разобьем каждое ребро параллелепипеда на равные части длины и через точки разбиения проведем плоскости, перпендикулярные к этому ребру. Параллелепипед разобьется На abc·103 n равных кубов с ребром Т.к. объем каждого такого куба равен , то объем всего параллелепипеда равен Итак, V = abc.

2 сл.Пусть a, b, c –бесконечные десятичные дроби. Рассмотрим конечные десятичные дроби an, bn, cn anbncn abc an’bn’cn’, где Объем V параллелепипеда Р заключен между Vn=anbncn и V’n= an’bn’cn’ т.е. anbncn V an’bn’cn’ Неограниченно увеличим n. Тогда число an’bn’cn’ будет мало отличаться от числа anbncn . V=abc. Ч.т.д

№ 650. Измерения прямоугольного параллелепипеда равны 8 см, 12 см и 18 см. найдите ребро куба, объем которого равен объему этого параллелепипеда Дано: прямоугольный параллелепипед. а = 8см, b = 12см, с = 8см Vпар= Vкуба Найти: d - ребро куба. Решение: V пар = abc=8·12·18=1728 cм 3. Vпар.=Vкуба= 1728 cм3= d3, d 3= 23·22·3·32·2=26·33, d=12 см. Ответ: 12 см.

№ 653. Диагональ прямоугольного параллелепипеда равна 18 см и составляет угол в 30 0 с плоскостью боковой грани и угол в 45 0 с боковым ребром. Найдите объем прямоугольного параллелепипеда. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед,. B1D - диагональ, B1D = 18 см, (B1D; (АВВ1)) = 30 0, B1D D 1 = 450 Найти: V параллелепипеда Решение 1 )Δ В1ВА – прямоугольный, т.к. В1В АВ (по условию АВСDA1B1C1D1 – прямоугольный параллелепипед). Δ B1AD -прямоульный, т.е. В1А = ПР (АА1В) B1D, (B1D; (AA1B1)) = DB1A = 300. 2) Δ B1AD - прямоугольный c углом в 300: AD= 9 см. 3) Δ B1D1D – прямоугольный, т.к. 4)По свойству диагонали прямоугольного параллелепипеда B1D2=AD2+DC2+DD12. Ответ: см3

Домашнее задание п. 63, п. 64 учить №654, №656