Презентация на тему: МНОГОГРАННИКИ

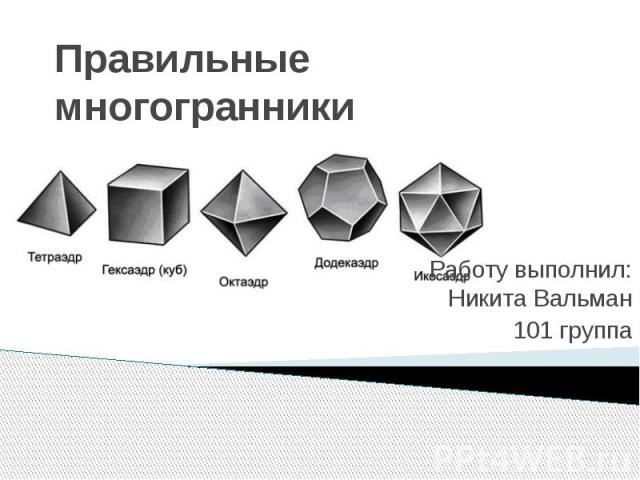
Правильные многогранники Работу выполнил: Никита Вальман 101 группа

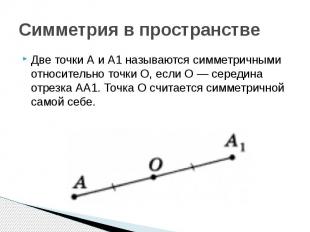
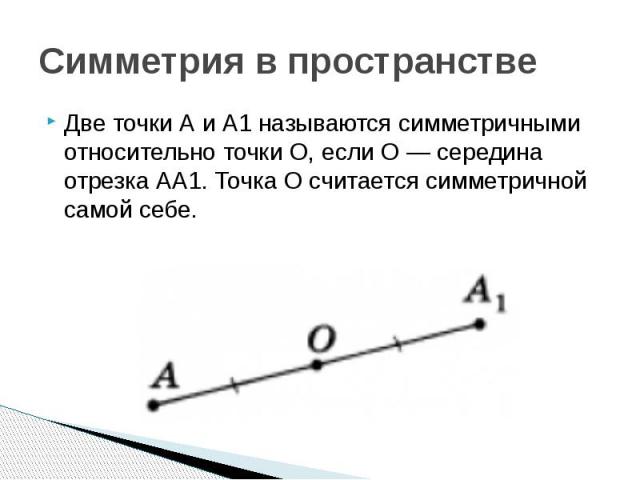
Симметрия в пространстве Две точки А и А1 называются симметричными относительно точки О, если О — середина отрезка АА1. Точка О считается симметричной самой себе.

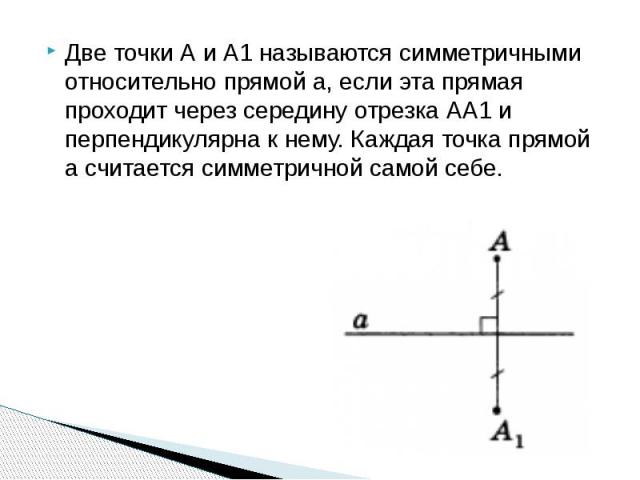
Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе. Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.

Две точки А и А1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости α считается симметричной самой себе. Две точки А и А1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости α считается симметричной самой себе.

Понятие правильного многогранника Правильный многогранник – это выпуклый многогранник с максимально возможной симметрией

Докажем, что не существует правильного многогранника, гранями которого являются n-угольники при n6. Из курса планиметрии вы знаете формулу для вычисления суммы внутренних углов выпуклого n-угольника: Sn =180°(n – 2), где n – число сторон, следовательно внутренний угол правильного многоугольника вычисляется по формуле: = При n6 120°, но при каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому, если бы существовал правильный многогранник, у которого грани – правильные n-угольники при n6, то сумма плоских углов при каждой вершине была бы не меньше 360°, а это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360°.

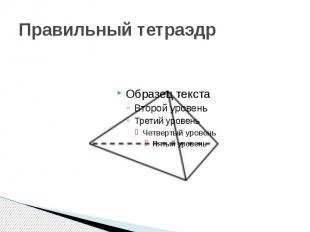
Правильный тетраэдр

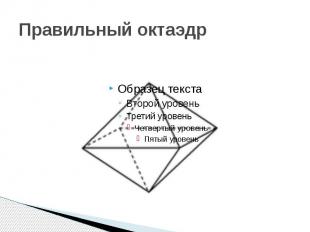
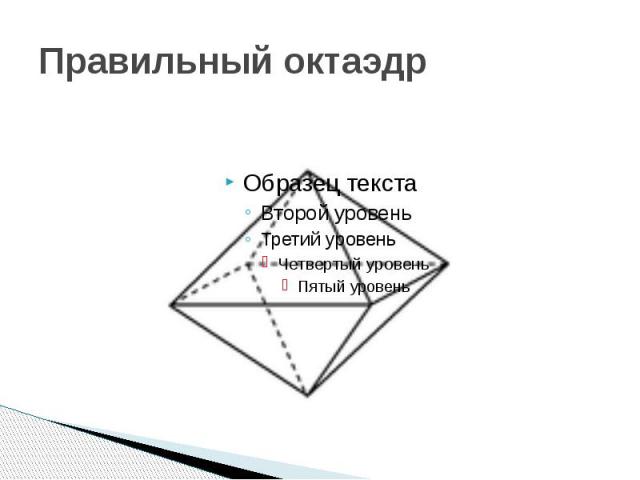
Правильный октаэдр

Правильный икосаэдр

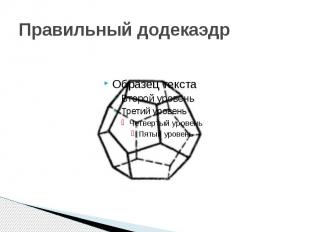
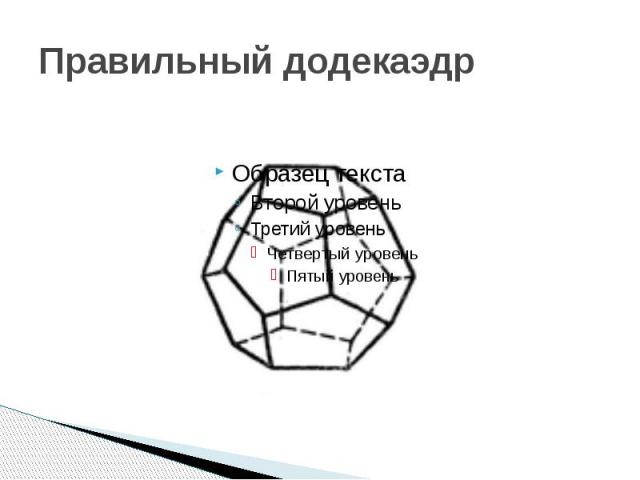
Правильный додекаэдр

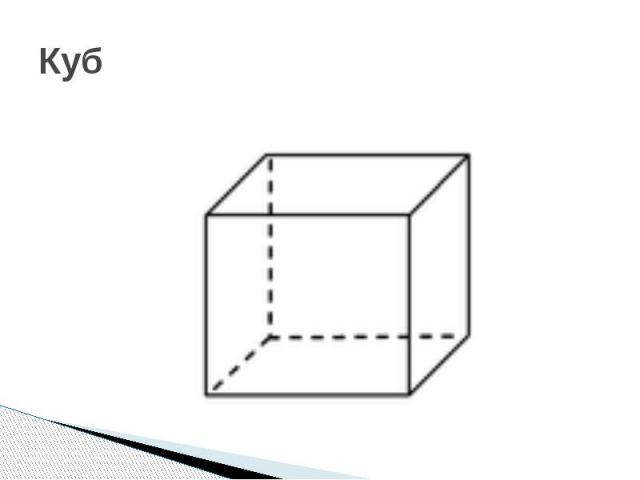
Куб

Элементы симметрии правильных многогранников Тетраэдр Центра симметрии тетраэдр не имеет. Правильный тетраэдр имеет 3 оси симметрии и шесть плоскостей симметрии. Куб У куба 1 центр симметрии - точка пересечения диагоналей куба. Куб имеет 9 плоскостей симметрии.

Правильный октаэдр, правильный икосаэдр и правильный додекаэдр Правильный октаэдр, правильный икосаэдр и правильный додекаэдр Имеют центр симметрии и несколько осей и плоскостей симметрии

Конец