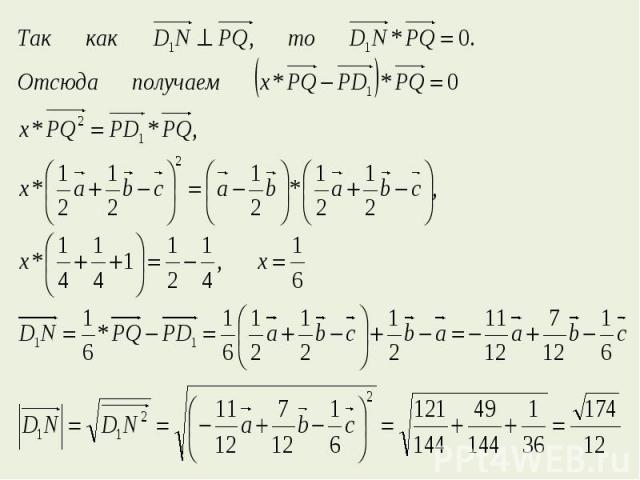Презентация на тему: Многогранники: виды задач и методы их решения (типовые задания С2) - 2

Многогранники: виды задач и методы их решения (типовые задания С2) - 2 Методическая разработка Амачкиной А.А.МОУ СОШ №12, г. Балашиха, Московской области.

1.2. Расстояние от точки до прямойРасстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра.Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.

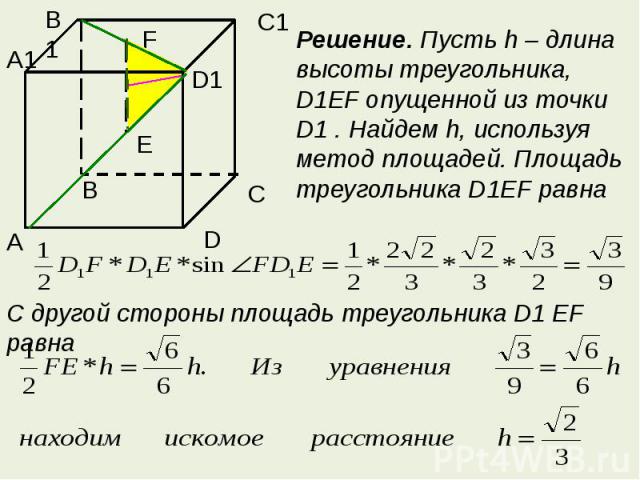
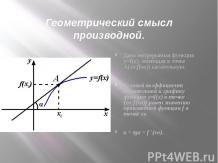
Поэтапно-вычислительный методРасстояние от точки до прямой можно вычислить, как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот.Пример 4. При условиях примера 1найти расстояние от точки D1 до прямой EF.

Решение. Пусть h – длина высоты треугольника, D1EF опущенной из точки D1 . Найдем h, используя метод площадей. Площадь треугольника D1EF равнаС другой стороны площадь треугольника D1 EF равна

Замечание. Можно заметить, что выполняется равенство FE2 +D1 E2 = D1 F 2,т.е. треугольник D1EF прямоугольный и длина отрезка D1 E является искомым расстоянием.

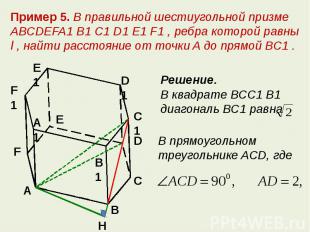
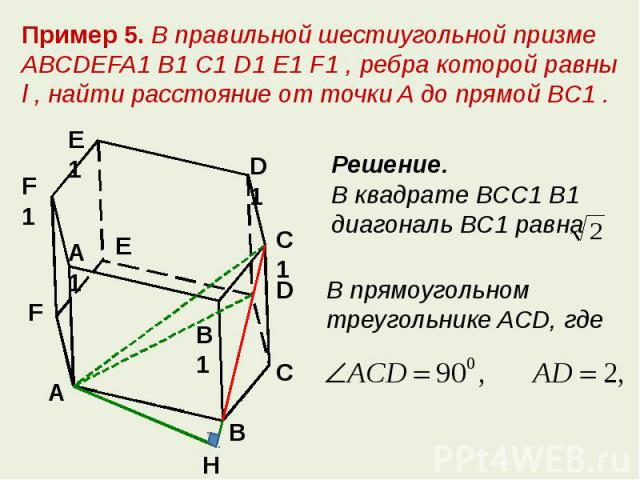
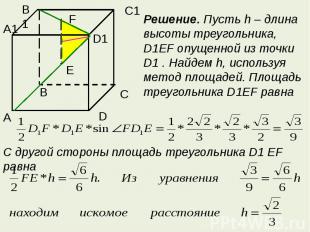
Пример 5. В правильной шестиугольной призме ABCDEFA1 B1 C1 D1 E1 F1 , ребра которой равны l , найти расстояние от точки A до прямой BC1 .Решение. В квадрате BCC1 B1 диагональ BC1 равнаВ прямоугольном треугольнике ACD, где

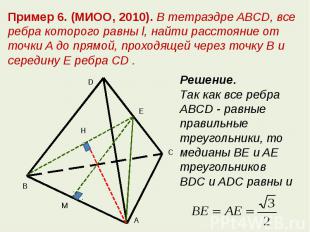
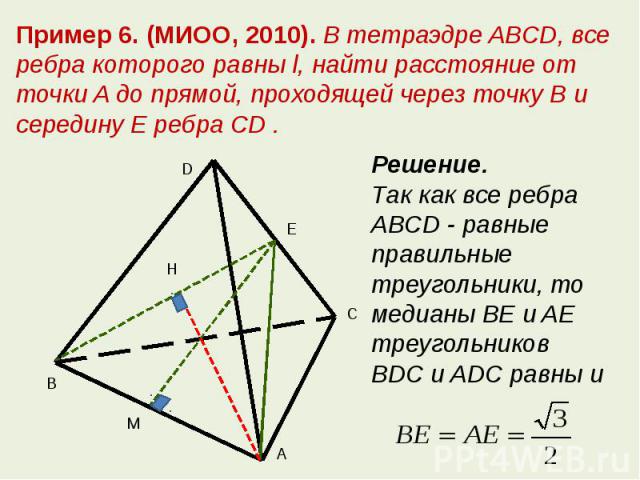
Пример 6. (МИОО, 2010). В тетраэдре ABCD, все ребра которого равны l, найти расстояние от точки A до прямой, проходящей через точку B и середину E ребра CD .Решение. Так как все ребра ABCD - равные правильные треугольники, то медианы BE и AE треугольников BDC и ADC равны и

Рассмотрим равнобедренный треугольник BEA и его высоты EM и AH. Выражая площадь треугольника двумя способами, получаем

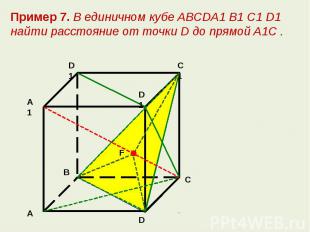
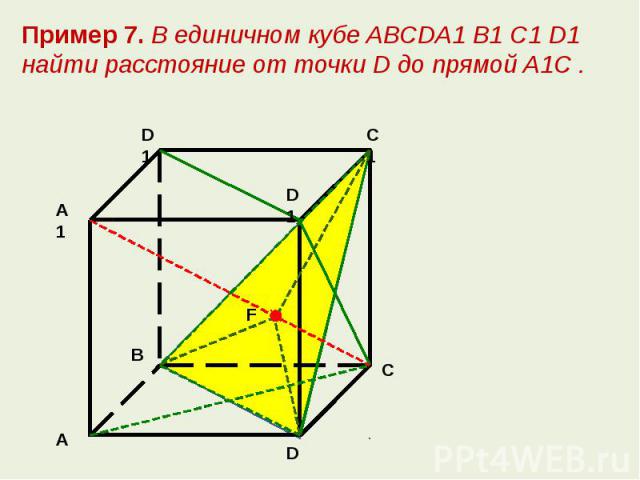
Пример 7. В единичном кубе ABCDA1 B1 C1 D1 найти расстояние от точки D до прямой A1C .

как проекции на плоскость BDC1 равных наклонных CC1 , СВ и CD соответственно. Следовательно, точка F является центром правильного треугольника BDC1 Поэтому искомое расстояние равно радиусу окружности, описанной около треугольника BDC1 .

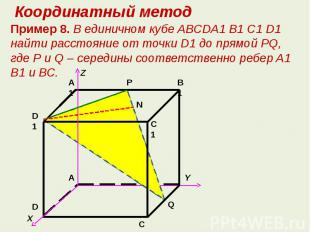
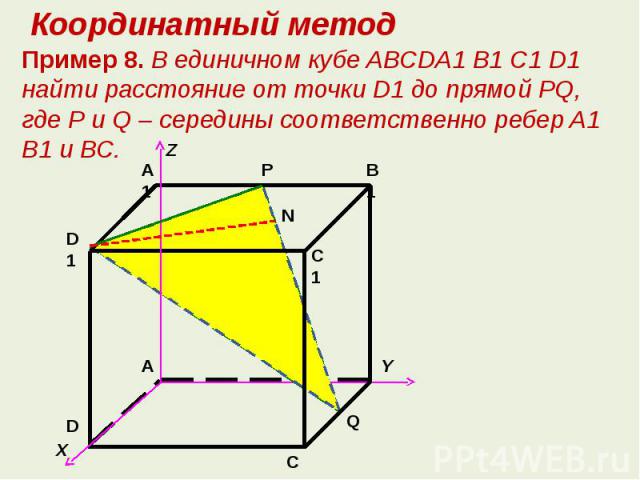
Координатный методПример 8. В единичном кубе ABCDA1 B1 C1 D1 найти расстояние от точки D1 до прямой РQ, где Р и Q – середины соответственно ребер A1 B1 и ВС.

Решение. Рассмотрим прямоугольную систему координат с началом в точке A Найдем координаты точекИз треугольника D1 PQ , используя формулу

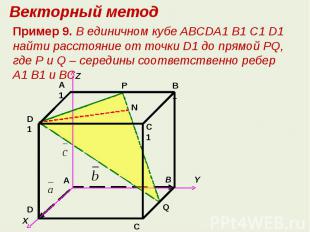
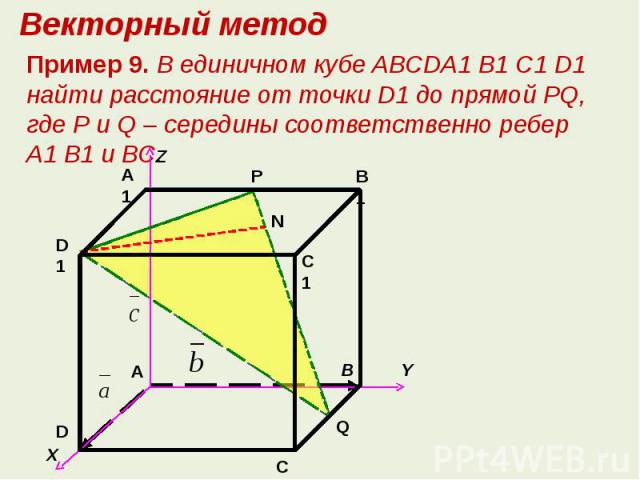
Векторный методПример 9. В единичном кубе ABCDA1 B1 C1 D1 найти расстояние от точки D1 до прямой РQ, где Р и Q – середины соответственно ребер A1 B1 и ВС.

Решение. Пусть

Замечание. Решение данного примера векторным методом не является рациональным, но приведено с целью показа широких возможностей векторного метода при решении задач разных видов

Используемая литература:Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.