Презентация на тему: Многогранники 9 класс

Цель: Собрать иллюстративный материал «Многогранники как геометрическая фигура». Систематизировать знания об основных видах многогранников. Связать эту тему с историей математики. Показать применение многогранников в других науках. Показать какую роль играет математики в развитии общества.

В природе существует много такого, что не может быть ни достаточно глубоко понято, ни достаточно убедительно доказано, ни достаточно умело и надежно использовано на практике без помощи вмешательства математики… В природе существует много такого, что не может быть ни достаточно глубоко понято, ни достаточно убедительно доказано, ни достаточно умело и надежно использовано на практике без помощи вмешательства математики… Ф.Бэкон

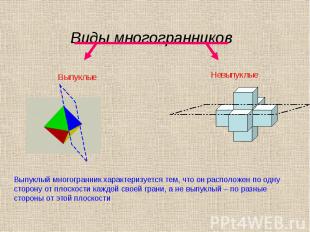
ПРАВИЛЬНЫЙ МНОГОГРАННИК- выпуклый многогранник, грани которого являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине которого сходится одно и то же число ребер.

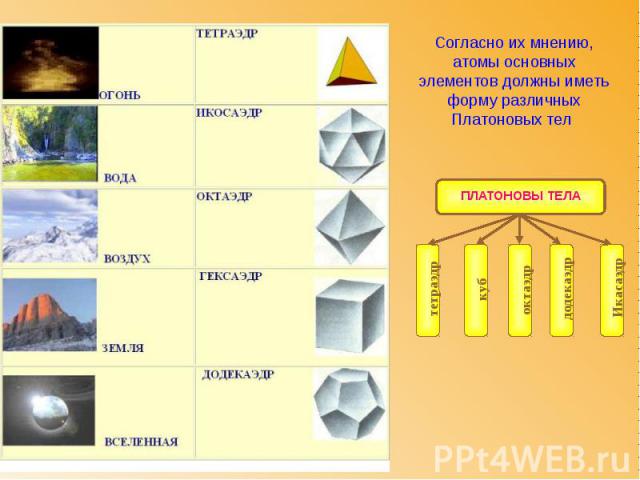
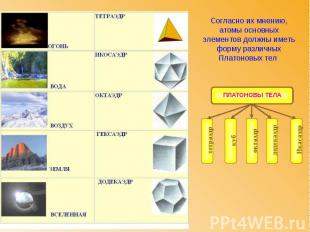
КУБ (ГЕКСАЭДР) Куб или гексаэдр – представитель платоновых тел, то есть правильных выпуклых многогранников. Куб имеет шесть квадратных граней, сходящихся в каждой вершине по три.

ОКТАЭДР Октаэдр – представитель семейства платоновых тел, то есть правильных выпуклых многогранников. Октаэдр имеет восемь треугольных граней, сходящихся в каждой вершине по четыре.

ДОДЕКАЭДР Додекаэдр – представитель семейства платоновых тел. Додекаэдр имеет двенадцать пятиугольных граней, сходящихся в вершинах по три. Этот многогранник замечателен своими тремя звездчатыми формами.

ИКОСАЭДР Икосаэдр – представитель платоновых тел. Поверхность икосаэдра состоит из двадцати равносторонних треугольников, сходящихся в каждой вершине по пять. Икосаэдр имеет одну звездчатую форму.

Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Два из них знал И. Кеплер (1571 – 1630 гг.). В 1812 году французский математик О. Коши доказал, что кроме пяти «платоновых тел» и четырех «тел Пуансо» больше нет правильных многогранников.

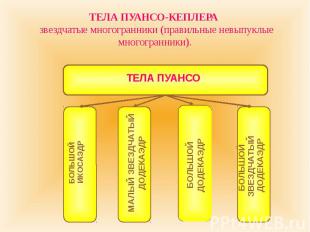
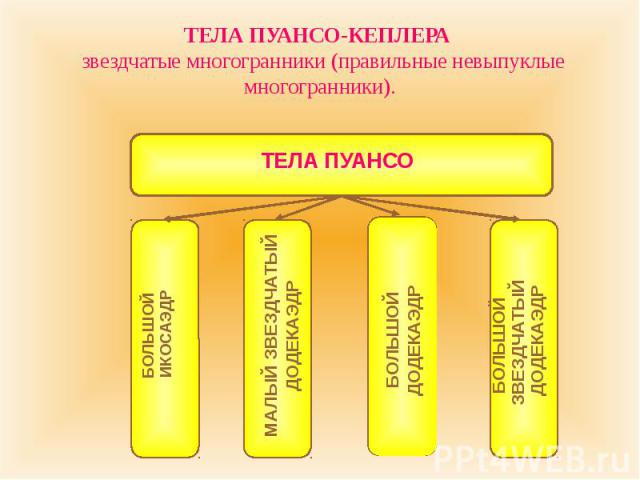
ТЕЛА ПУАНСО-КЕПЛЕРА звездчатые многогранники (правильные невыпуклые многогранники).

БОЛЬШОЙ ИКОСАЭДР Грани большого икосаэдра - пересекающиеся треугольники. Вершины большого икосаэдра совпадают с вершинами описанного икосаэдра. Большой икосаэдр был впервые описан Луи Пуансо в 1809 г.

МАЛЫЙ ЗВЕЗДЧАТЫЙ ДОДЕКАЭДР Грани малого звездчатого додекаэдра - пентаграммы, как и у большого звездчатого додекаэдра. У каждой вершины соединяются пять граней. Вершины малого звездчатого додекаэдра совпадают с вершинами описанного икосаэдра. Малый звездчатый додекаэдр был впервые описан Кеплером в 1619 г.

БОЛЬШОЙ ДОДЕКАЭДР Грани большого додекаэдра - пересекающиеся пятиугольники. Вершины большого додекаэдра совпадают с вершинами описанного икосаэдра. Большой додекаэдр был впервые описан Луи Пуансо в 1809 г.

БОЛЬШОЙ ЗВЕЗДЧАТЫЙ ДОДЕКАЭДР Грани большого звездчатого додекаэдра - пентаграммы, как и у малого звездчатого додекаэдра. У каждой вершины соединяются три грани. Вершины большого звездчатого додекаэдра совпадают с вершинами описанного додекаэдра. Большой звездчатый додекаэдр был впервые описан Кеплером в 1619 г.

ТЕЛА АРХИМЕДА полуправильные однородные выпуклые многогранники

Первую группу составляют пять многогранников, которые получаются из пяти платоновых тел в результате их усечения: Первую группу составляют пять многогранников, которые получаются из пяти платоновых тел в результате их усечения:

Вторую группу составляют два тела, называемых квазиправильными многогранниками. Это название означает, что гранями этого многогранника являются правильные многоугольники всего двух типов, причем каждая грань одного типа окружена гранями другого типа. Эти два тела называются Вторую группу составляют два тела, называемых квазиправильными многогранниками. Это название означает, что гранями этого многогранника являются правильные многоугольники всего двух типов, причем каждая грань одного типа окружена гранями другого типа. Эти два тела называются

В третью группу входят В третью группу входят ромбокубоктаэдр, который иногда называют малым ромбокубоктаэдром и ромбоикосододекаэдр, называемый также малым ромбоикосододекаэдром. В эту же группу входят ромбоусеченный кубоктаэдр, иногда называемый большим ромбокубоктаэдром и ромбоусеченный икосододекаэдр, называемый также большим ромбоикосододекаэдром, которые получаются из кубоктаэдра и икосододекаэдра при другом варианте усечения.

В четвертую группу входят две курносые модификации - курносый куб и курносый додекаэдр. В четвертую группу входят две курносые модификации - курносый куб и курносый додекаэдр. Для них характерно несколько повернутое положение граней. В результате эти многогранники, в отличие от предыдущих, не имеют плоскостей симметрии, но имеют оси симметрии. Так как плоскостей симметрии нет, то зеркальное отражение такого тела не совпадает с исходным телом, и поэтому существуют по две формы каждого из них - "правая" и "левая", отличающиеся так же, как правая и левая руки.

Рекомендации Данный материал являющийся полноценным дидактическим материалом можно использовать на уроках геометрии с (8 по 11 класс) истории изобразительного искусства черчении МХК (мировой художественной культуре)

Перспективы Работа над теоретическим материалом по теме: Формулы площадей, объемов многогранников, построение сечений, т.е. формирование практической базы для старших классов. Рассмотрение расширения областей применения многогранников, например, в химии, биологии, медицине, экономике.

Спасибо за внимание ! Спасибо за внимание !