Презентация на тему: Координаты вектора в пространстве

Векторы в пространстве

Это учебник создан для экзамена по геометрии. В нем рассмотрена темы 10-го класса- Векторы в пространстве, и действия над векторами в пространстве. Уверена вам понравится!!!

Абсолютная величина и направление вектора. Векторы в пространстве Действия над векторами: Тест Об авторе

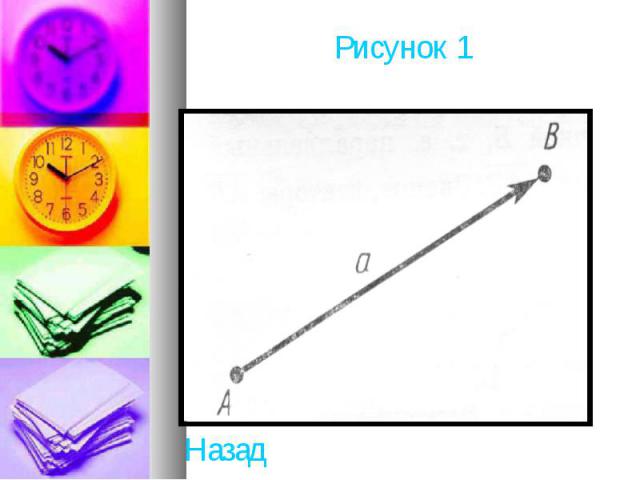
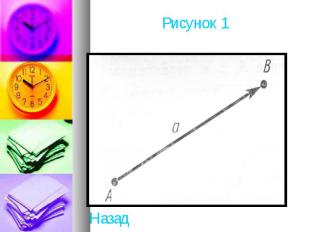
Вектором мы будем называть направленный отрезок (рисунок 1) . Направление вектора определяется указанием его начала и конца. На чертеже направление вектора отмечается стрелкой. Для обозначения векторов будем пользоваться строчными латинскими буквами а, Ь, с, ... . Можно также обозначить вектор указанием его начала и конца. При этом начало вектора ставится на первом месте. Вместо слова «вектор» над буквенным обозначением вектора иногда ставится стрелка или черта. Вектор на рисунке 1 можно обозначить так: или

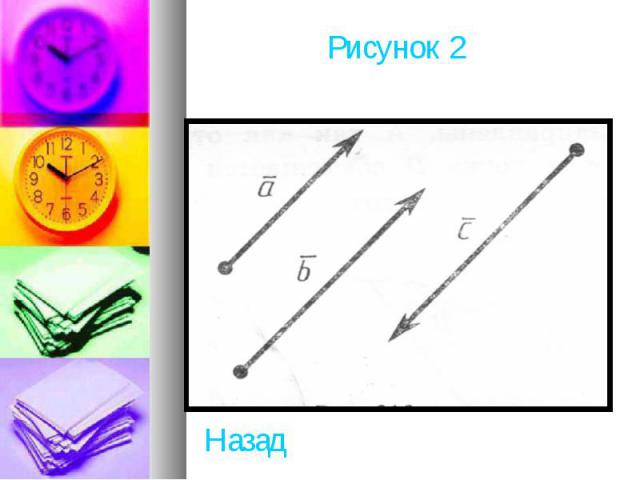
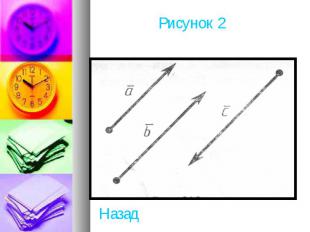
Векторы называются одинаково направленными, если полупрямые АВ и СD одинаково направлены. Векторы называются противоположно направленными, если полупрямые АВ и СD противоположно направлены. На рисунке 212 векторы одинаково направлены, а векторы противоположно направлены. Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора а обозначается . Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается нулем с черточкой . О направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю(Рисунок 2) .

В пространстве, как и на плоскости, вектором называется направленный отрезок. Буквально так же, как и на плоскости, определяются основные понятия для векторов в пространстве: абсолютная величина вектора, направление вектора, равенство векторов. Координатами вектора с началом в точке А1(х1; у1; z1) и концом в точке А2(х2;y2;z2) называются числа х2 - х1, у2 - у1, z2 - z1. Так же, как и на плоскости, доказывается, что равные векторы имеют соответственно равные координаты и, обратно, векторы с соответственно равными координатами равны. Это дает основание для обозначения вектора его координатами: а (a1, a2; а3) или просто (а1; а2; а3).

Так же, как и на плоскости, определяются действия над векторами: сложение, разность , умножение на число и скалярное произведение.

Суммой векторов (a1; а2; а3) и (b1; b2; b3) называется вектор: (a1 + b1; а2 + b2; а3 + b3). Так же,как и на плоскости, доказывается векторное равенство (доказательство) :

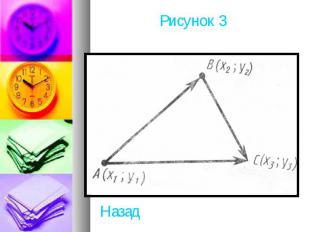
Пусть A (х1; у1),В(х2; у2),С(х3; у3) -данные точки (рисунок 3) .Вектор имеет координаты х2-х1,y2-y1, вектор имеет координаты х3 - х2, у3-y2. Следовательно, вектор имеет координаты х3-х1, у3-у1. А это есть координаты вектора . Значит, векторы равны. Теорема доказана.

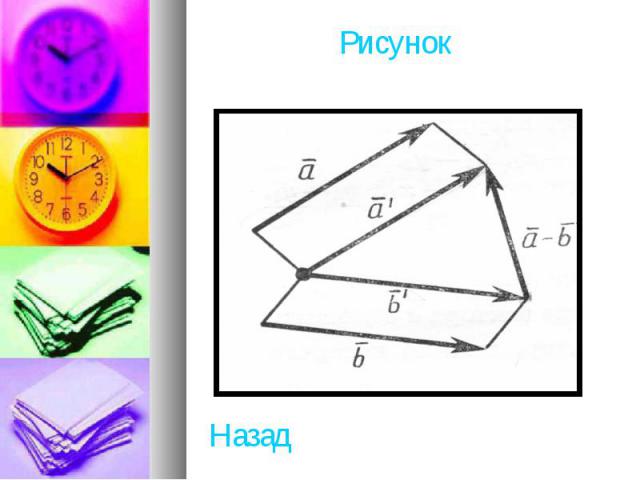
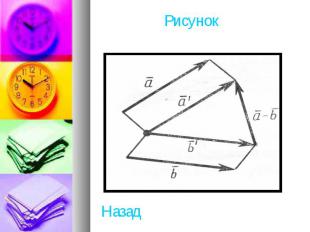
Разностью векторов (а1;а2;a3) и (b1; b2;b3) называется такой вектор (с1; с2;c3), который в сумме с вектором дает вектор : Ь . Отсюда находим координаты вектора : c1=a1-b1;c2=a2-b2;c3=a3-b3

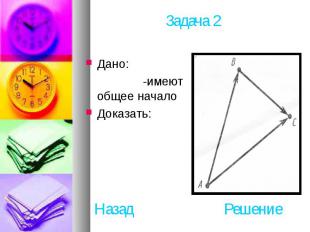
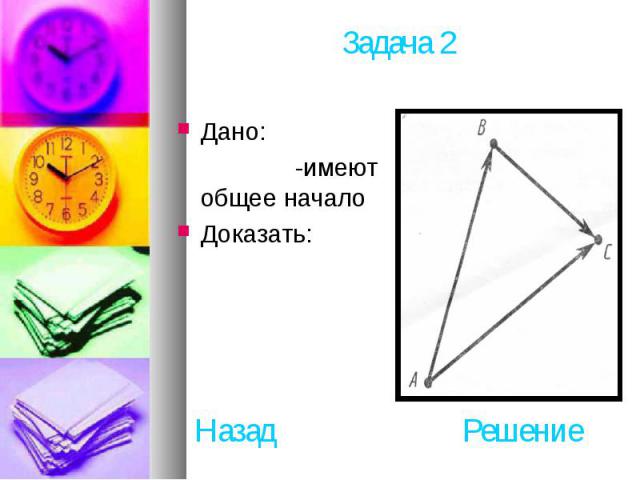
Дано: -имеют общее начало Доказать:

Дано: A(2;7;-3) B(1;0;3) C(-3;-4;5) D(-2;3;-1) Найти: Среди всех векторов указать равные

Дано: (1;2;3) Найти: Коллинеарный вектор с началом в точке A(1;1;1) и концом B на плоскости xy.

Произведением вектора а(a1; а2; a3) на число λ называется вектор Так же, как и на плоскости, доказывается, что абсолютная величина вектора λа равна \λ\ \ \, а направление совпадает с направлением вектора , если λ> 0, и противоположно направлению вектора , если λ<0.

Скалярным произведением векторов и называется число a1b1 +a2b2 +a3b3. Буквально так же, как и на плоскости, доказывается, что скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между векторами.

Дано: A(0;1;-1) B(1;-1;2) C(3;1;0) D(2;-3;1) Найти: cosφ=?