Презентация на тему: Двугранный угол, перпендикулярность плоскостей

5klass.net

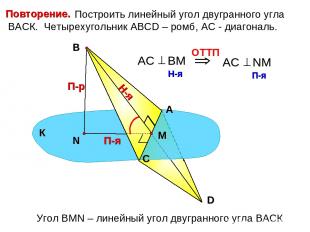
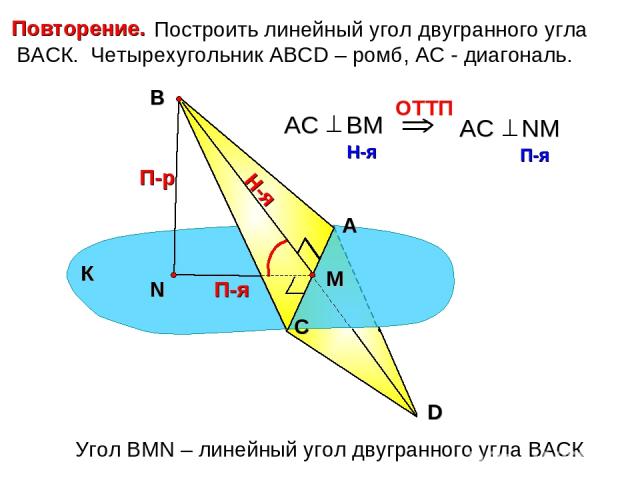
Построить линейный угол двугранного угла ВАСК. Четырехугольник АВСD – ромб, АС - диагональ. А С В П-р Н-я П-я Угол ВMN – линейный угол двугранного угла ВАСК К D Повторение.

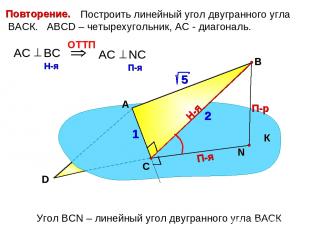
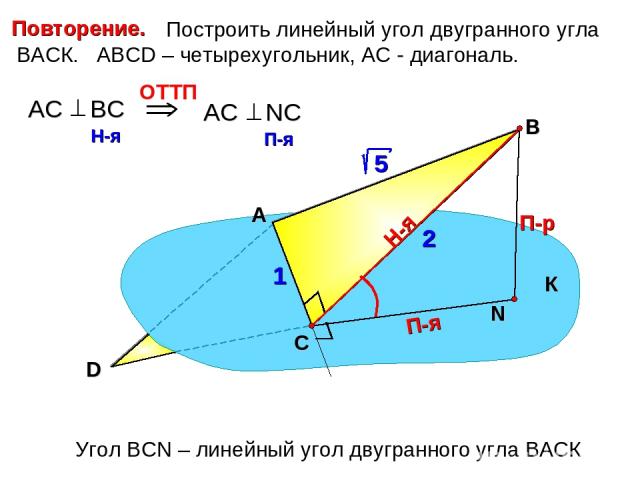
Построить линейный угол двугранного угла ВАСК. АВСD – четырехугольник, АС - диагональ. А В П-р Н-я П-я Угол ВСN – линейный угол двугранного угла ВАСК К С D 2 1 Повторение.

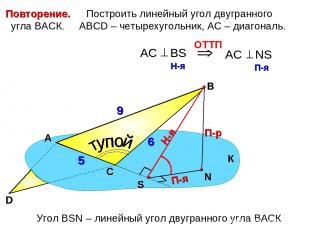
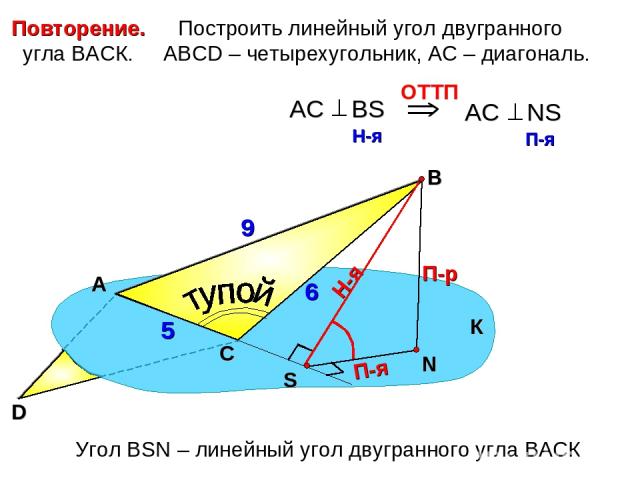
Построить линейный угол двугранного угла ВАСК. АВСD – четырехугольник, АС – диагональ. А В П-р Н-я П-я Угол ВSN – линейный угол двугранного угла ВАСК К С D 9 6 5 Повторение.

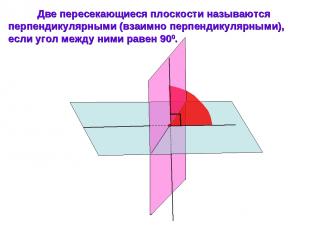
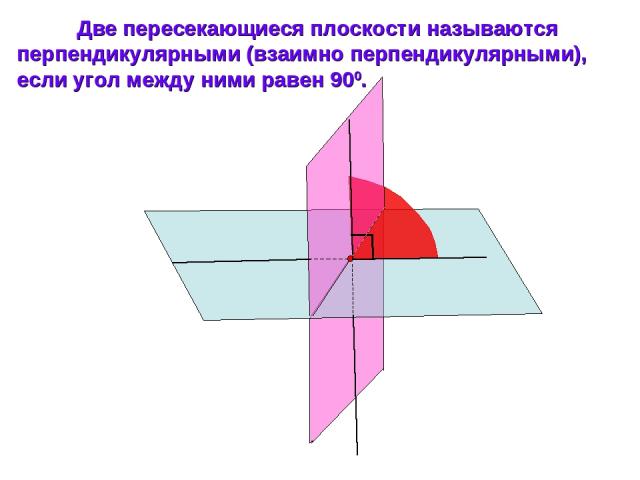
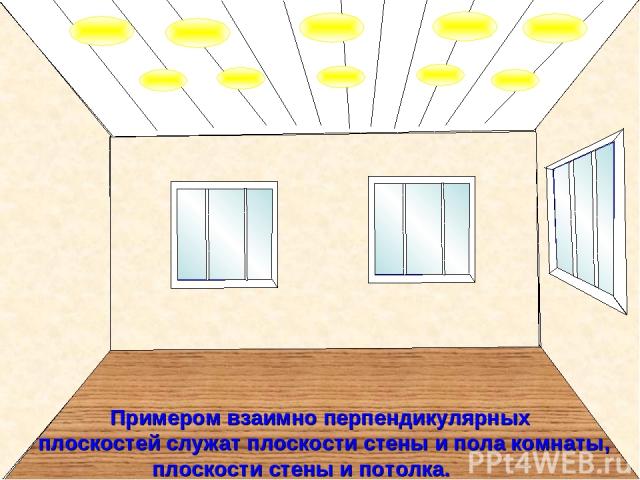
Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900.

Примером взаимно перпендикулярных плоскостей служат плоскости стены и пола комнаты, плоскости стены и потолка.

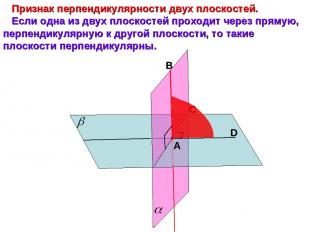
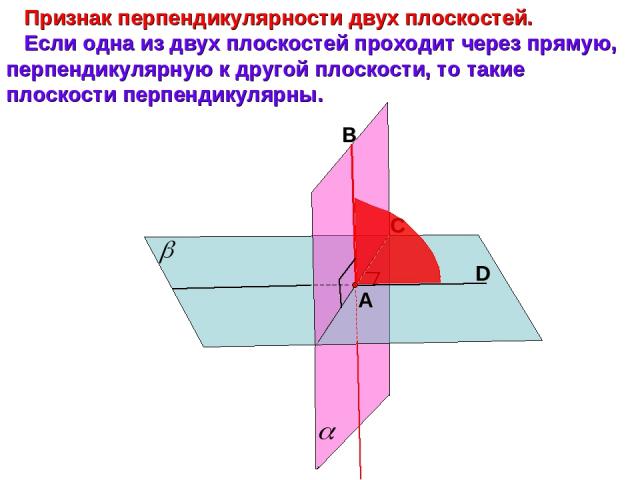
Признак перпендикулярности двух плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны. А С

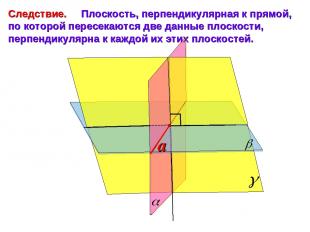
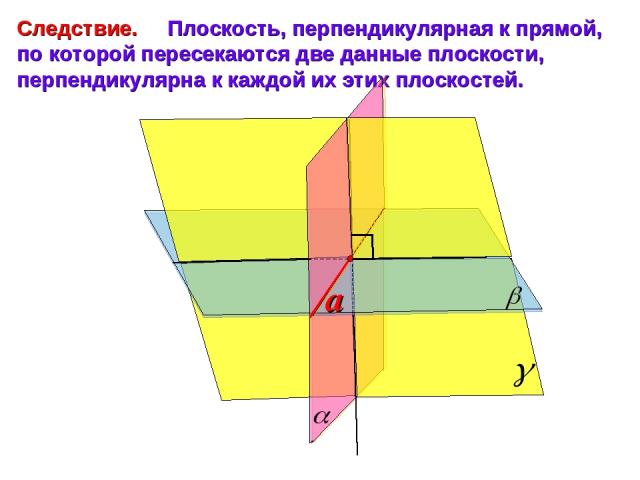
Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой их этих плоскостей.

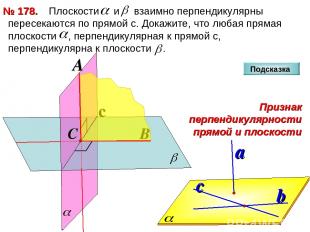
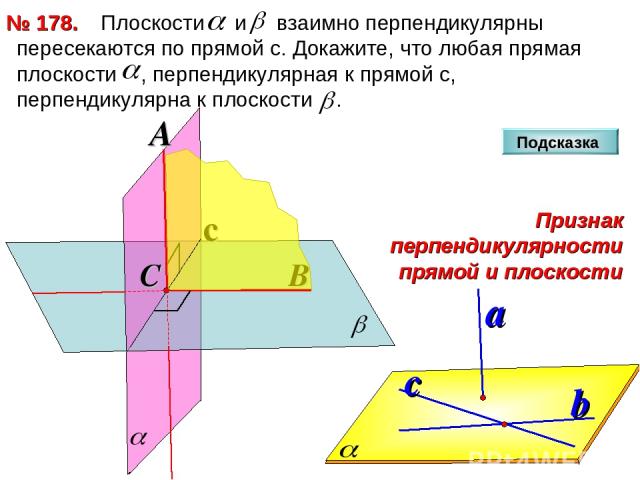
Плоскости и взаимно перпендикулярны пересекаются по прямой с. Докажите, что любая прямая плоскости , перпендикулярная к прямой с, перпендикулярна к плоскости . № 178. c C Подсказка

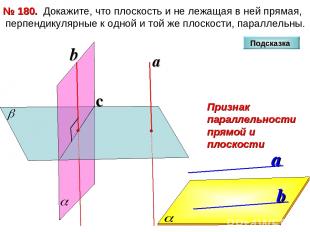
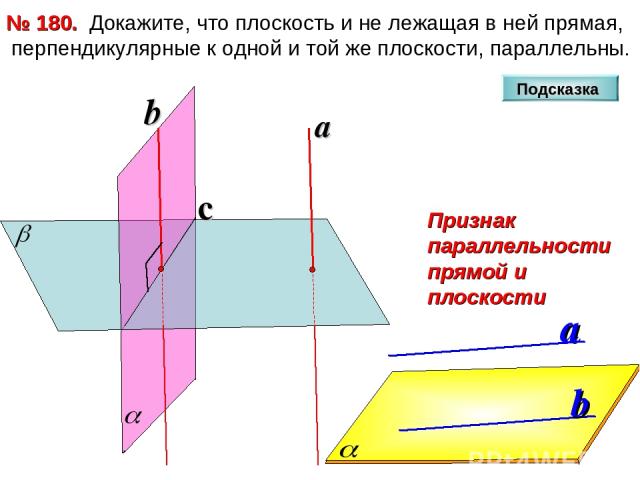
Докажите, что плоскость и не лежащая в ней прямая, перпендикулярные к одной и той же плоскости, параллельны. № 180. c Подсказка

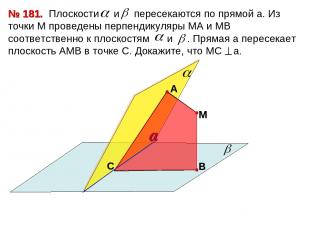
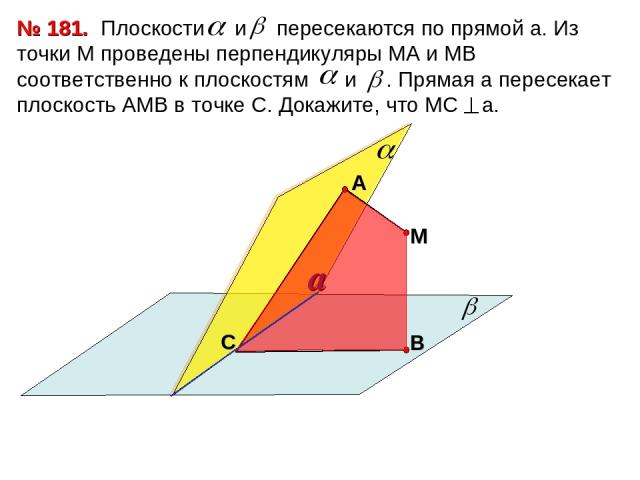
№ 181. С М a

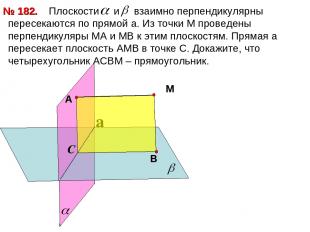
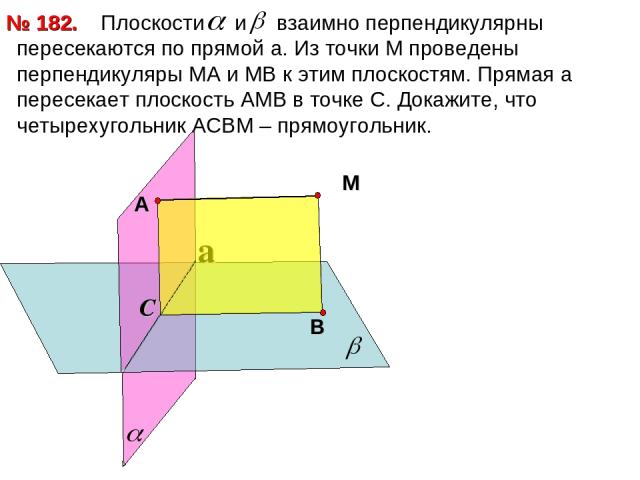
Плоскости и взаимно перпендикулярны пересекаются по прямой a. Из точки М проведены перпендикуляры МА и МВ к этим плоскостям. Прямая а пересекает плоскость АМВ в точке С. Докажите, что четырехугольник АСВМ – прямоугольник. № 182. a С М

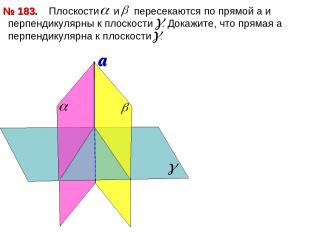
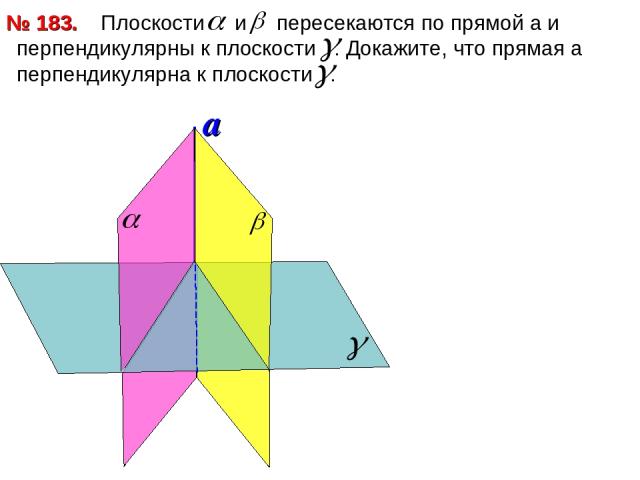
Плоскости и пересекаются по прямой a и перпендикулярны к плоскости . Докажите, что прямая а перпендикулярна к плоскости . № 183.

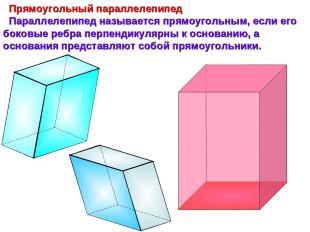
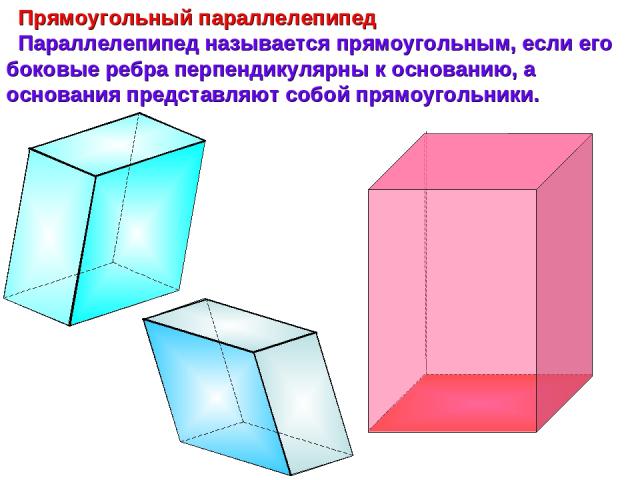
Прямоугольный параллелепипед Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

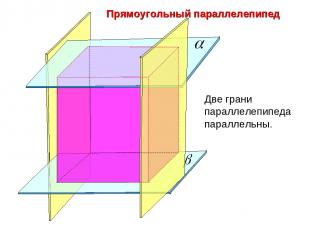
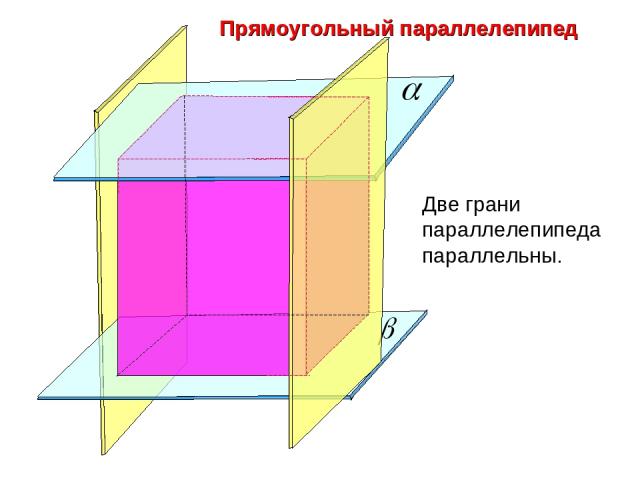
Прямоугольный параллелепипед Две грани параллелепипеда параллельны.

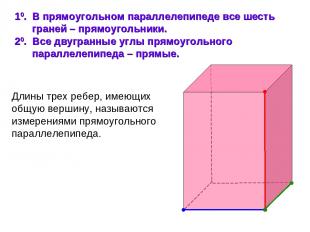
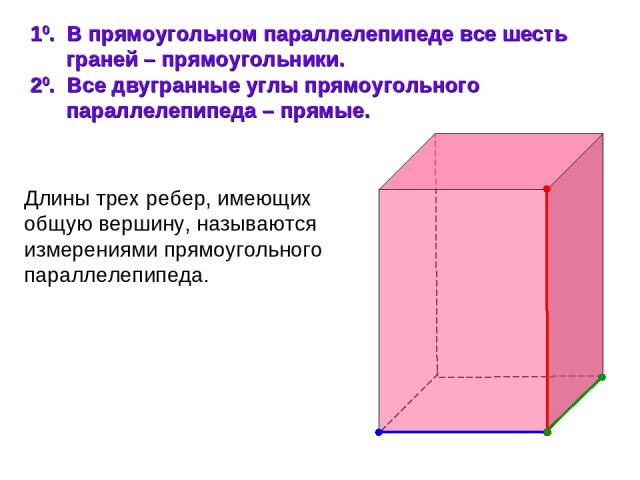
10. В прямоугольном параллелепипеде все шесть граней – прямоугольники. 20. Все двугранные углы прямоугольного параллелепипеда – прямые. Длины трех ребер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.

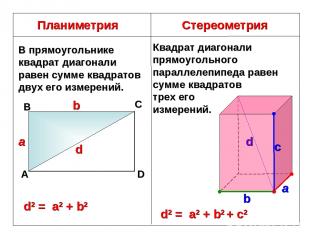
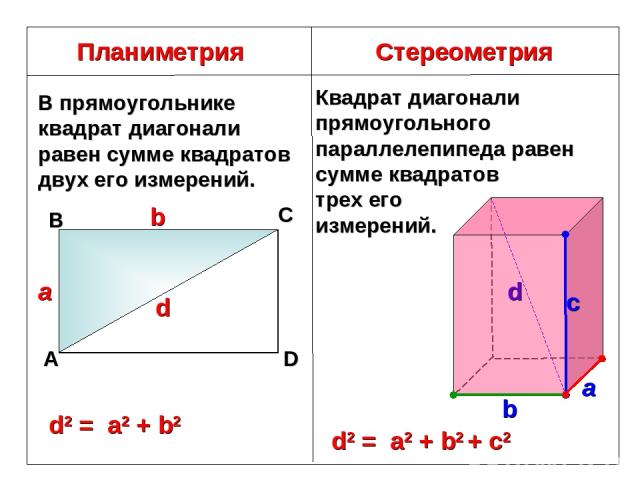
Планиметрия Стереометрия В прямоугольнике квадрат диагонали равен сумме квадратов двух его измерений. А В С D d a b d2 = a2 + b2 Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. d2 = a2 + b2 + с2

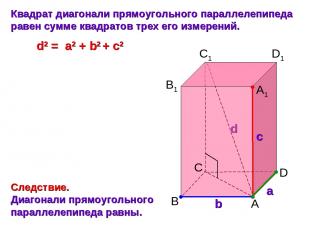
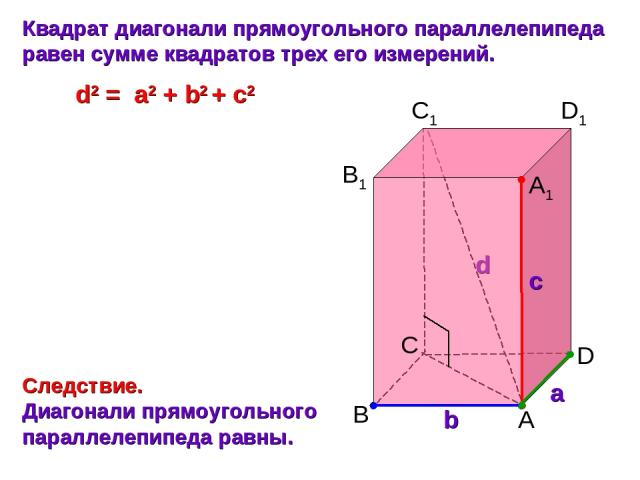
C а b с B A D B1 C1 D1 A1 Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Следствие. Диагонали прямоугольного параллелепипеда равны. d2 = a2 + b2 + с2

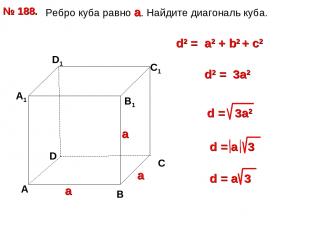
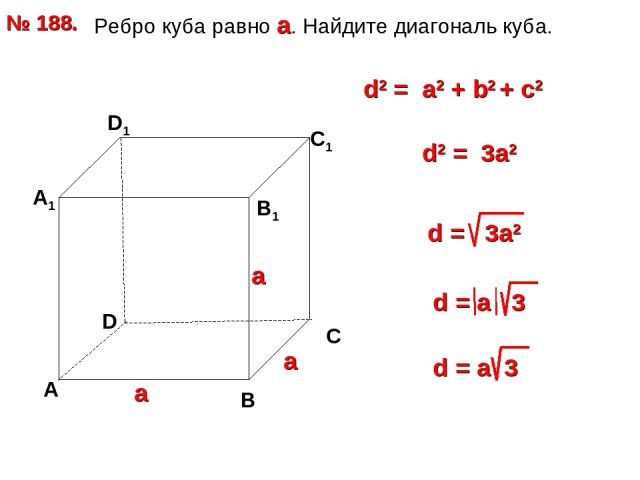
Ребро куба равно а. Найдите диагональ куба. № 188. D А В С А1 D1 С1 В1 d2 = a2 + b2 + с2 d2 = 3a2 а а а

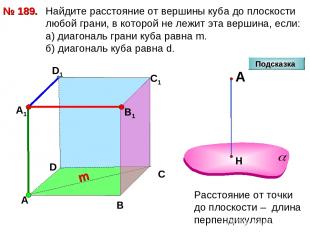
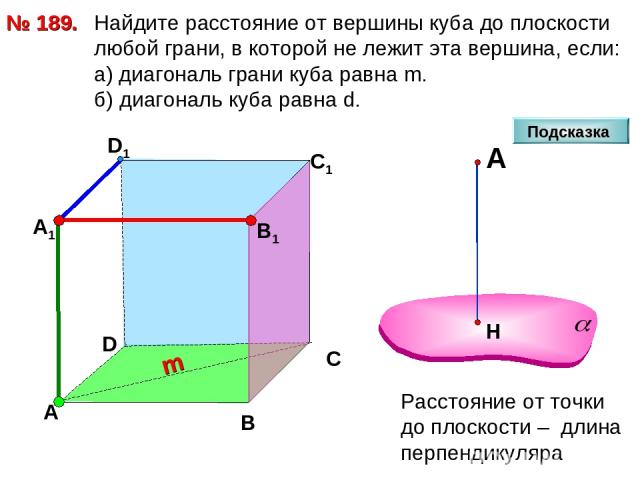
Найдите расстояние от вершины куба до плоскости любой грани, в которой не лежит эта вершина, если: а) диагональ грани куба равна m. б) диагональ куба равна d. № 189. D А В С D1 С1 m Подсказка В1 А1

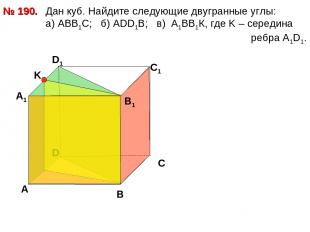
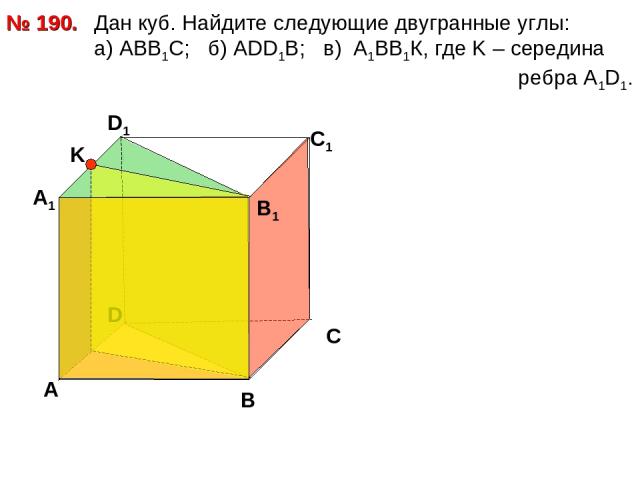
Дан куб. Найдите следующие двугранные углы: a) АВВ1С; б) АDD1B; в) А1ВВ1К, где K – середина ребра А1D1. № 190. D А В С А1 D1 С1 В1

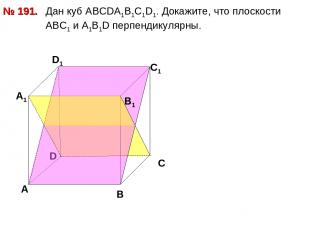
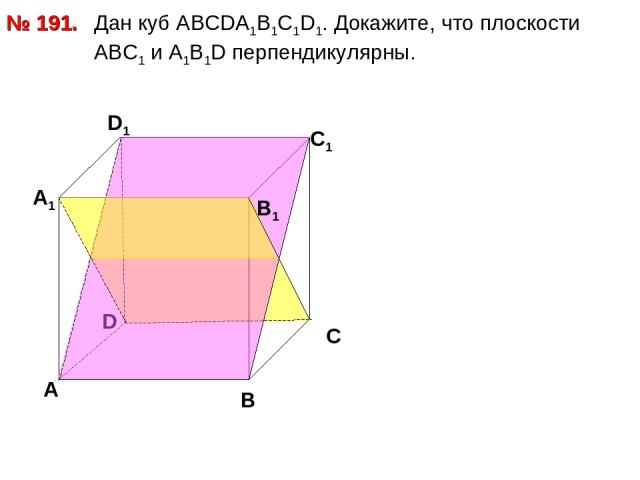
Дан куб АВСDА1В1С1D1. Докажите, что плоскости АВС1 и А1В1D перпендикулярны. № 191. D А В С А1 D1 С1 В1

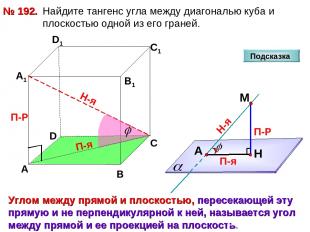
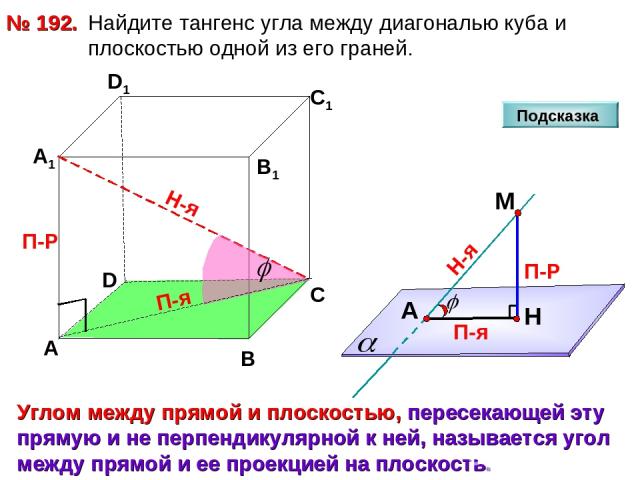
Найдите тангенс угла между диагональю куба и плоскостью одной из его граней. № 192. D А В С А1 D1 С1 В1 Подсказка П-Р Н-я

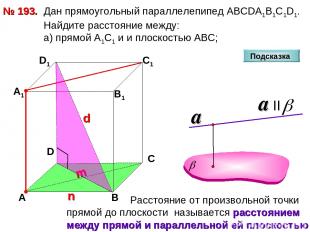
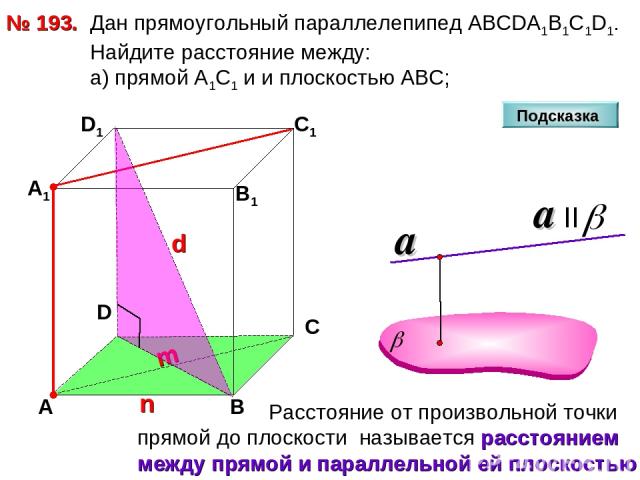
№ 193. D А В С А1 D1 С1 В1 Подсказка Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите расстояние между: а) прямой А1С1 и и плоскостью АВС;

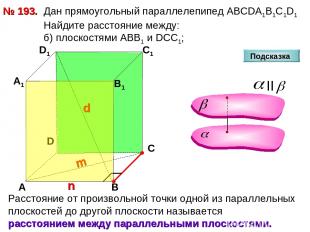
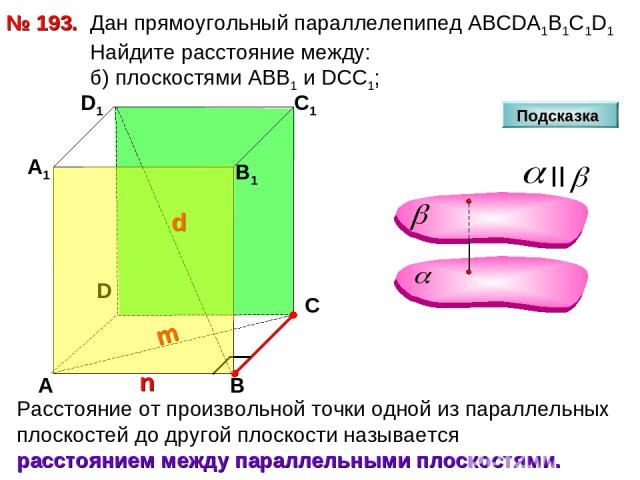
№ 193. D А В С А1 D1 С1 В1 Подсказка Дан прямоугольный параллелепипед АВСDА1В1С1D1 Найдите расстояние между: б) плоскостями АВВ1 и DCC1;

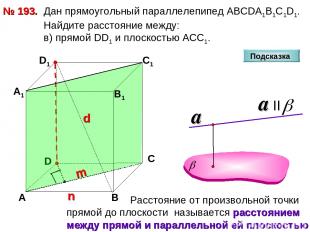
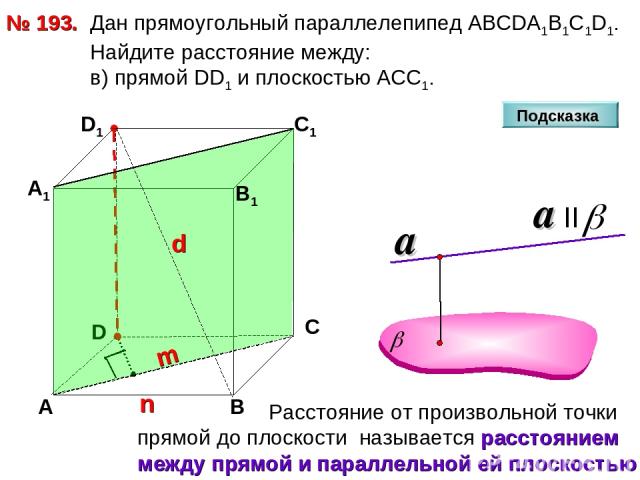
№ 193. D А В С А1 D1 С1 Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите расстояние между: в) прямой DD1 и плоскостью АСС1. Подсказка В1

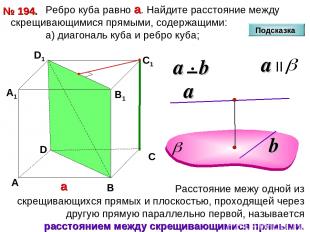
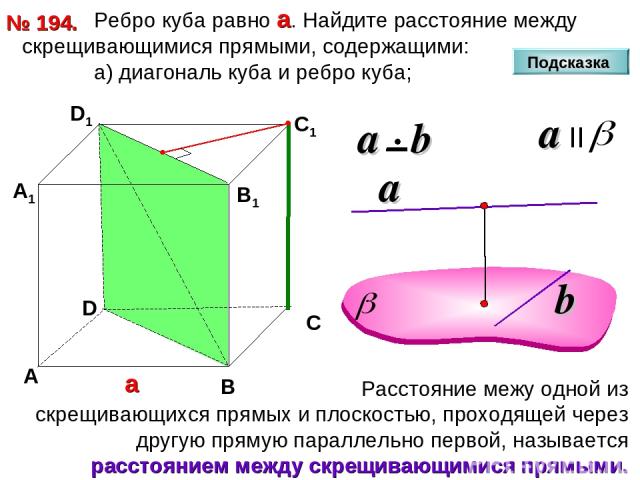
Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащими: а) диагональ куба и ребро куба; № 194. D А В С D1 С1 а В1 А1 Подсказка

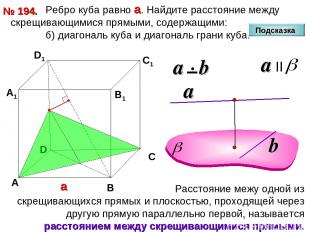
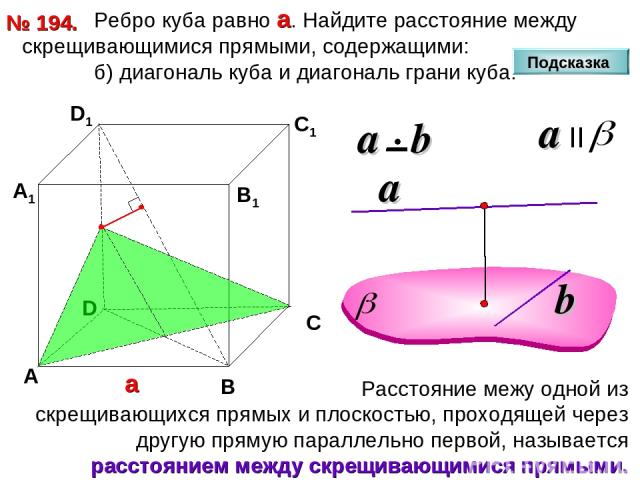
Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащими: б) диагональ куба и диагональ грани куба. № 194. D А В С D1 С1 а В1 А1 Подсказка

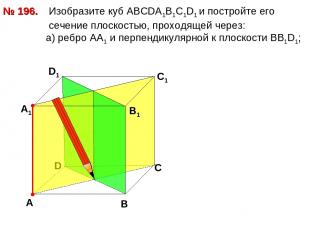
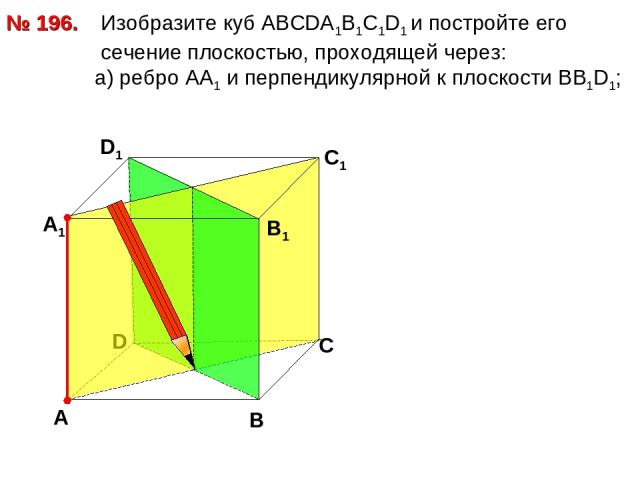
№ 196. D В D1 С1 Изобразите куб АВСDА1В1С1D1 и постройте его сечение плоскостью, проходящей через: а) ребро АА1 и перпендикулярной к плоскости ВВ1D1; А А1 С В1

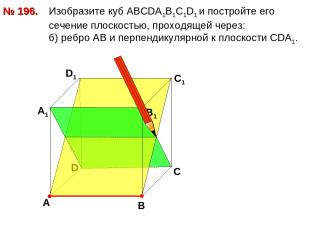
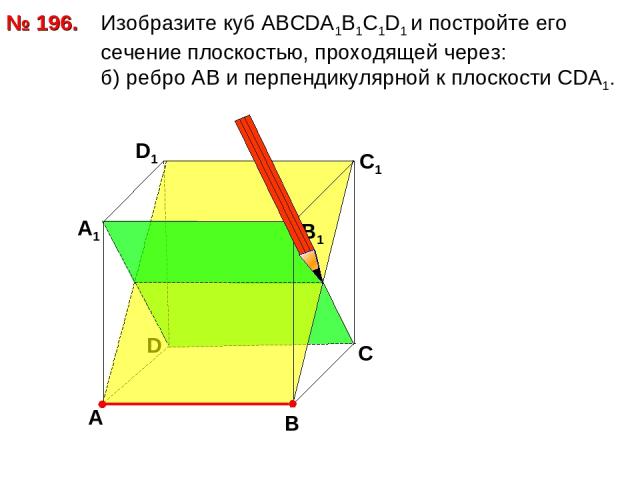
№ 196. Изобразите куб АВСDА1В1С1D1 и постройте его сечение плоскостью, проходящей через: б) ребро АВ и перпендикулярной к плоскости СDA1. D В D1 С1 А А1 В1 С

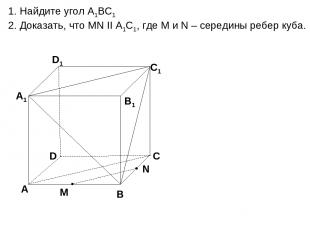
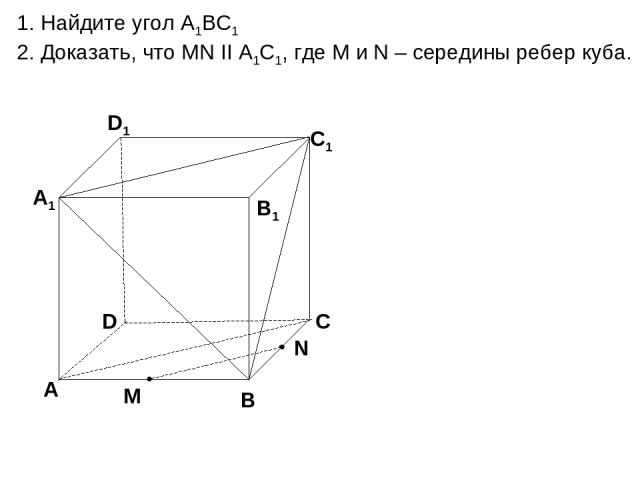
D А В С А1 D1 С1 В1 1. Найдите угол А1ВС1 2. Доказать, что MN II А1С1, где M и N – середины ребер куба.

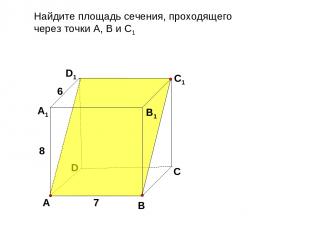
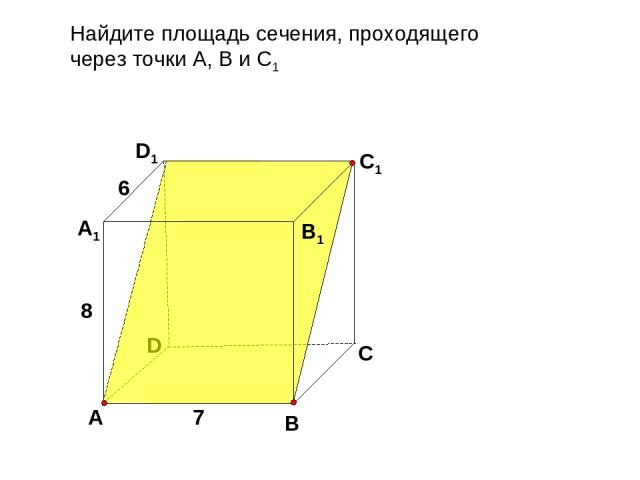
Найдите площадь сечения, проходящего через точки А, В и С1 D В D1 С1 А А1 В1 С 7 8 6