Презентация на тему: Двугранный угол геометрия

Геометрия 10 «А» класс 18.03.2008 900igr.net

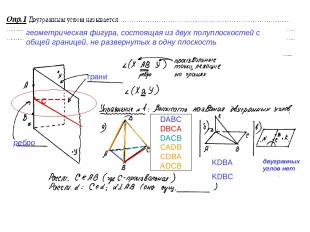
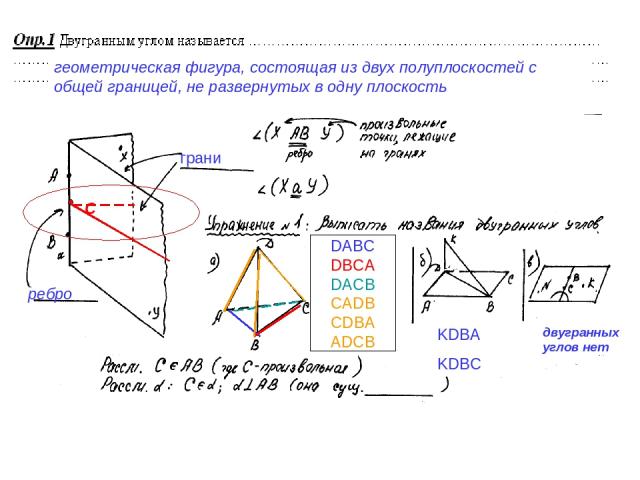
геометрическая фигура, состоящая из двух полуплоскостей с общей границей, не развернутых в одну плоскость DABC DBCA DACB CADB CDBA ADCB ребро грани KDBA KDBC двугранных углов нет

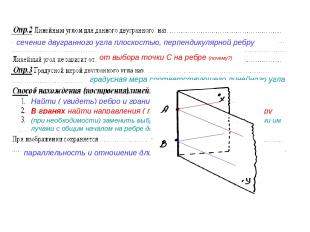
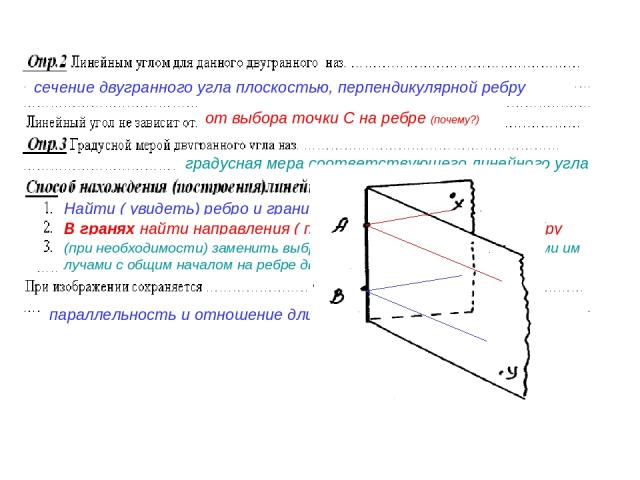
сечение двугранного угла плоскостью, перпендикулярной ребру от выбора точки С на ребре (почему?) градусная мера соответствующего линейного угла Найти ( увидеть) ребро и грани двугранного угла В гранях найти направления ( прямые) перпендикулярные ребру (при необходимости) заменить выбранные направления параллельными им лучами с общим началом на ребре двугранного угла параллельность и отношение длин параллельных отрезков

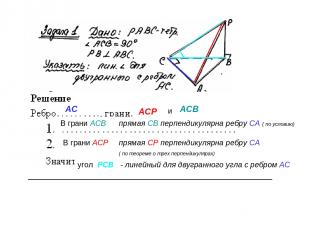
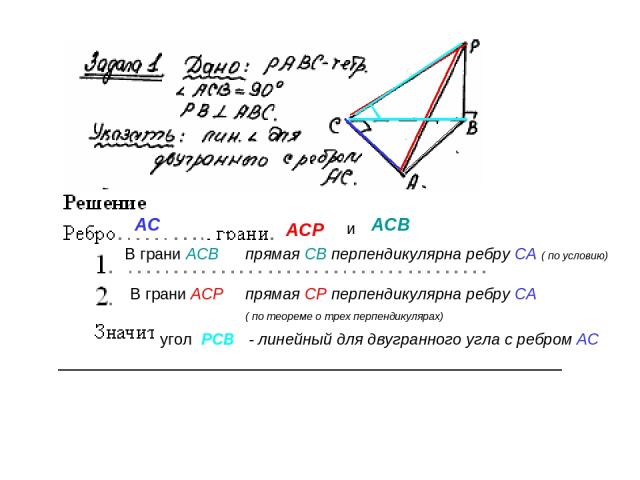
АС АСР АСВ и В грани АСВ В грани АСР угол РСВ - линейный для двугранного угла с ребром АС АСВ прямая СВ перпендикулярна ребру СА ( по условию) прямая СР перпендикулярна ребру СА ( по теореме о трех перпендикулярах)

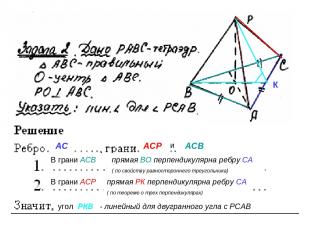
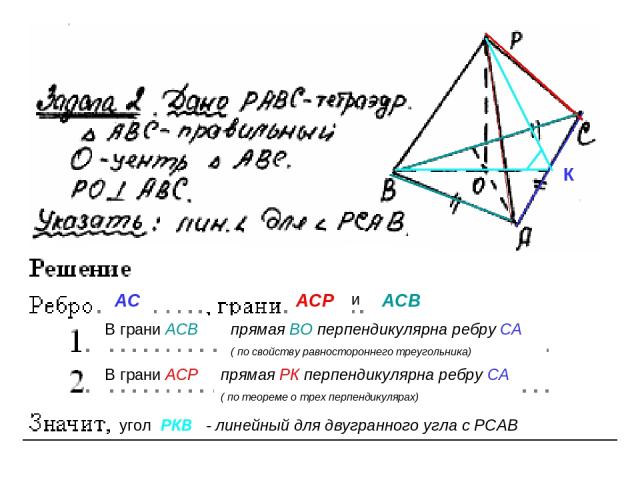
АС АСР и АСВ В грани АСВ К В грани АСР угол РКВ - линейный для двугранного угла с РСАВ прямая ВО перпендикулярна ребру СА ( по свойству равностороннего треугольника) прямая РК перпендикулярна ребру СА ( по теореме о трех перпендикулярах)

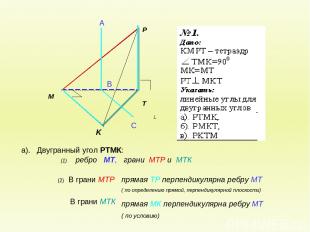
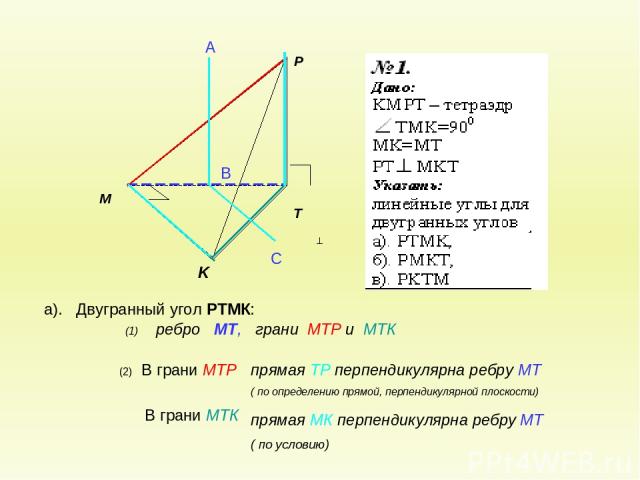
а). Двугранный угол РТМК: (2) В грани МТР В грани МТК А В С (1) ребро МТ, грани МТР и МТК прямая ТР перпендикулярна ребру МТ ( по определению прямой, перпендикулярной плоскости) прямая МК перпендикулярна ребру МТ ( по условию)

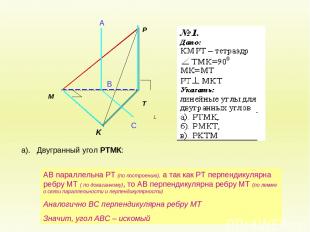
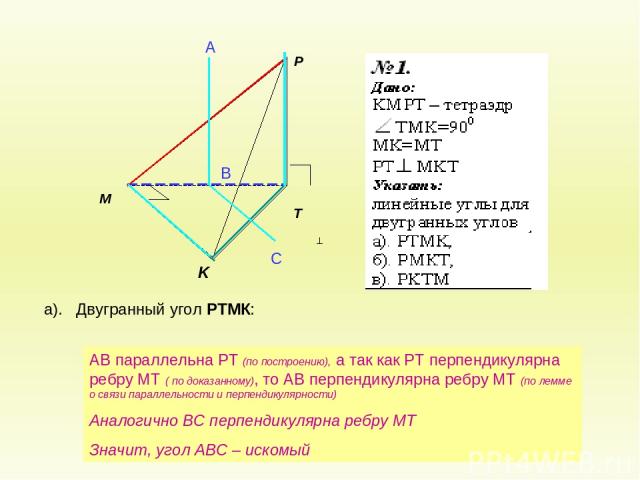
а). Двугранный угол РТМК: А В С АВ параллельна РТ (по построению), а так как РТ перпендикулярна ребру МТ ( по доказанному), то АВ перпендикулярна ребру МТ (по лемме о связи параллельности и перпендикулярности) Аналогично ВС перпендикулярна ребру МТ Значит, угол АВС – искомый

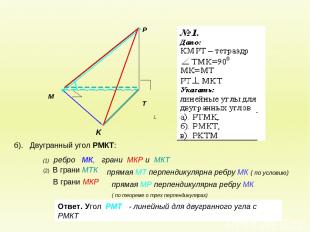
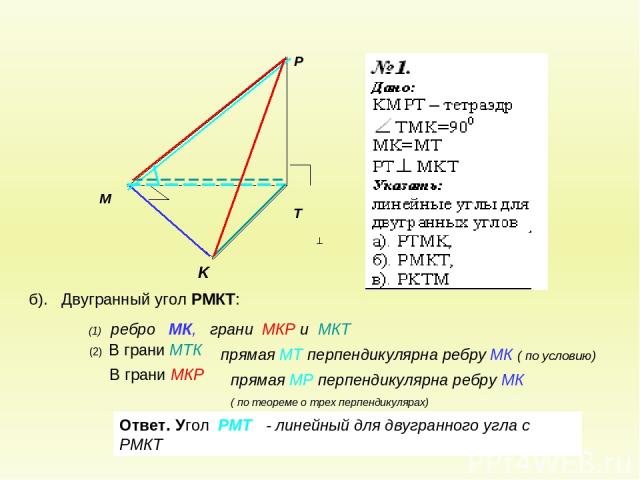
б). Двугранный угол РМКТ: В грани МКР (2) В грани МТК Ответ. Угол РМТ - линейный для двугранного угла с РМКТ (1) ребро МК, грани МКР и МКТ прямая МТ перпендикулярна ребру МК ( по условию) прямая МР перпендикулярна ребру МК ( по теореме о трех перпендикулярах)

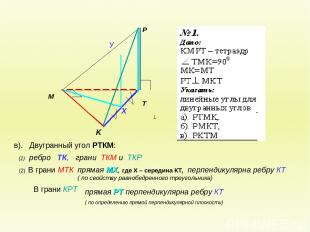
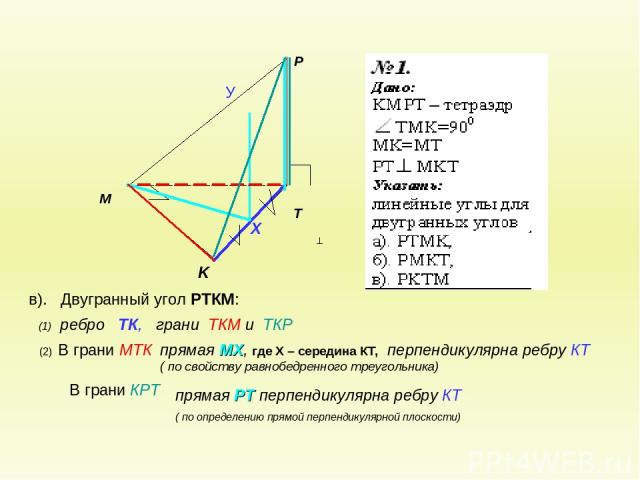
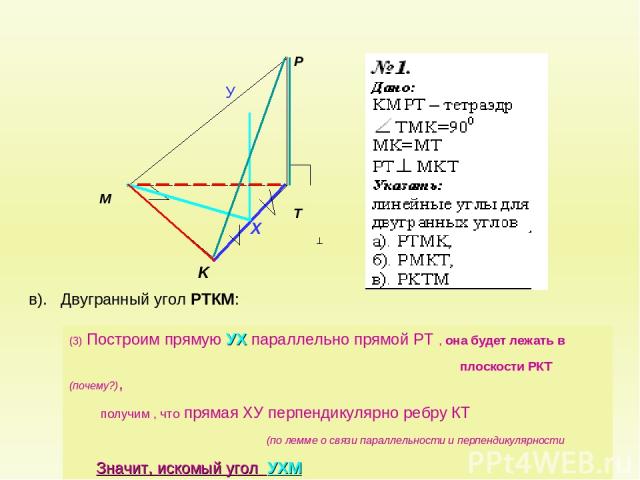
в). Двугранный угол РТКМ: В грани КРТ (2) В грани МТК (1) ребро ТК, грани ТКМ и ТКР прямая МХ, где Х – середина КТ, перпендикулярна ребру КТ ( по свойству равнобедренного треугольника) прямая РТ перпендикулярна ребру КТ ( по определению прямой перпендикулярной плоскости)

в). Двугранный угол РТКМ: (3) Построим прямую УХ параллельно прямой РТ , она будет лежать в плоскости РКТ (почему?), получим , что прямая ХУ перпендикулярно ребру КТ (по лемме о связи параллельности и перпендикулярности Значит, искомый угол УХМ

Пример вычислительной задачи по теме «Двугранный угол»

Для тех, кто недостаточно хорошо справился с задачами урока, предлагается необязательное домашнее задание: Сделать модели к зачетным задачам №1-4 ( см. стр.2-4 конспекта), изменив названия вершин и положение тетраэдра, но не меняя отличительных черт задачи: например, в задаче №1 в основании тетраэдра должен лежать прямоугольный равнобедренный треугольник, а вершина должна проектироваться в одну из вершин острого угла основания. К модели приложить запись решения задачи. Модель может быть как объемной, так и складной. Своей моделью можно будет пользоваться на зачете. 2. Оформить решение задачи, аналогичной разобранной зачетной задачи №1, в виде презентации. 3. Придумать несколько задач, аналогичных зачетным задачам №1 и №2, и оформить каждую из них по образцу на стр.2-3 конспекта. Каждая страница оценивается максимальным баллом 1. Нормы оценок по количеству сданных страниц. Геометрия 10. тема « Двугранный угол»

Теоретические вопросы опроса для 1 подгруппы Определение двугранного угла Определение градусной меры двугранного угла Определение линейного угла для данного двугранного Утверждение о количестве линейных углов для данного двугранного Способ построения линейного угла Особенности изображения пространственных геометрических фигур на плоскости