Презентация на тему: Тригонометрические функции 10 класс
Презентация на тему: «Тригонометрические функции» Цель: напомнить сведения о тригонометрических функциях, полученные в 9 классе, подготовить к изучению новых сведений и свойств тригонометрических функций.
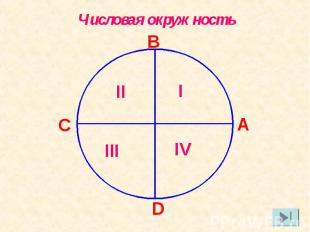
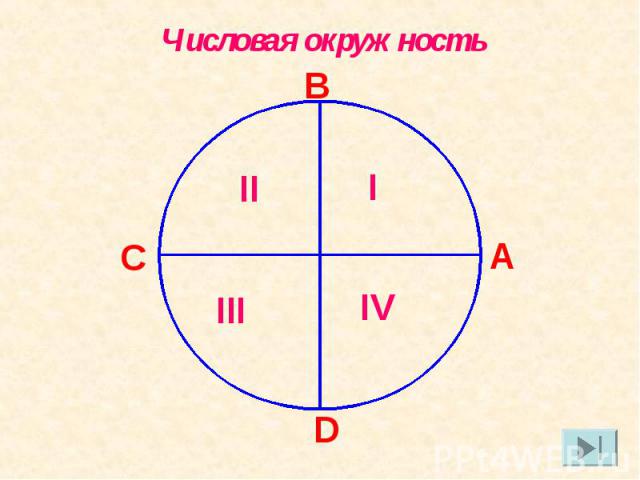
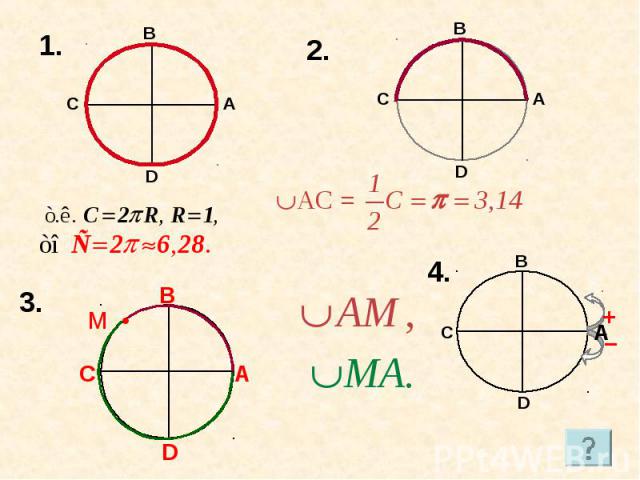
Числовая окружность

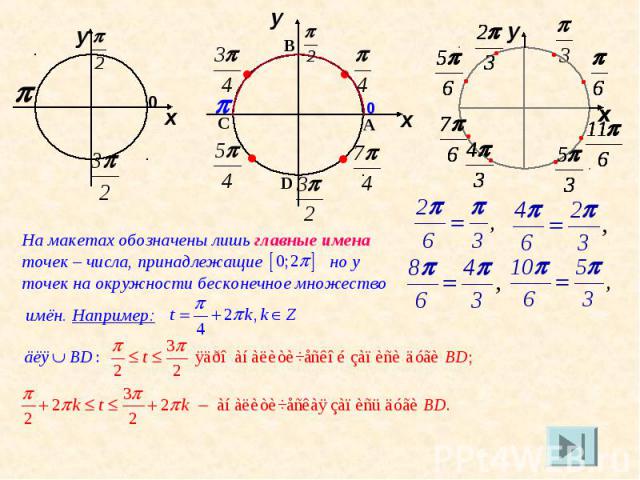
На макетах обозначены лишь главные имена точек – числа, принадлежащие но у точек на окружности бесконечное множество имён. Например:

Всем числам со знаменателем 4 соответствуют декартовы координаты с точностью до знака в зависимости от четверти, в которой расположена точка.

Синус, косинус, тангенс и котангенс

Свойства синуса, косинуса, тангенса и котангенса

Основные тригонометрические формулы
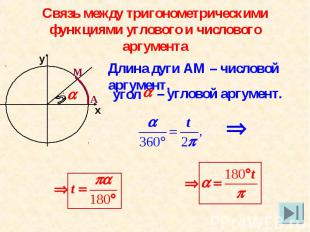
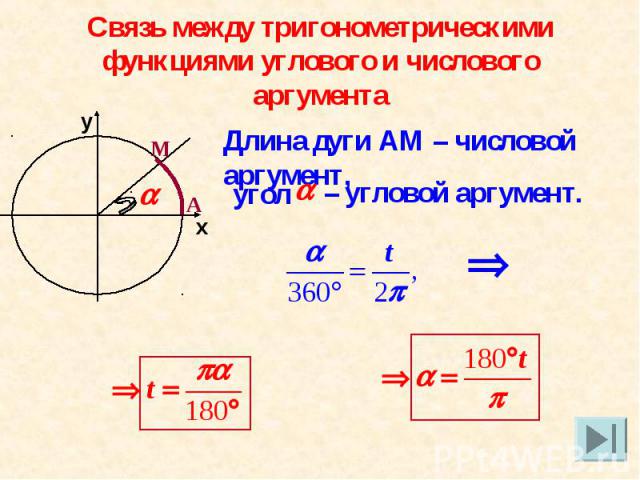
Связь между тригонометрическими функциями углового и числового аргументаДлина дуги АМ – числовой аргумент, – угловой аргумент.

Угол в 1 рад – это центральный угол , длина дуги которого равна радиусу окружности. Таким образом, в тригонометрии независимую переменную мы можем считать числовым аргументом или угловым аргументом.

Значения тригонометрических функций

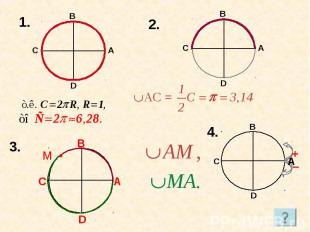
Тренировочные упражненияТочка М делит дугу АВ в отношении 2 : 3. найти длину дуг: а) АМ; б) МВ; в) DM; г) МС Точка Р делит третью четверть в отношении 1 : 5. Найдите длину дуги СР, РD, АР.
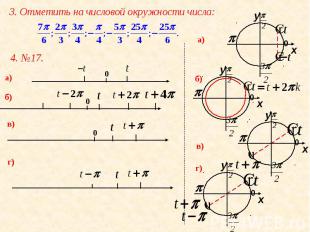
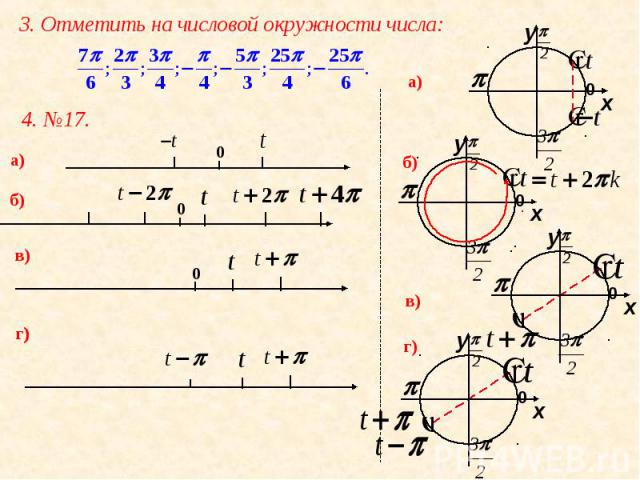
3. Отметить на числовой окружности числа:

Итог урокаЧисловая окружность, радиус, четверти. Длина окружности. Положительное и отрицательное направление обхода. Имена точек на числовой окружности. Какие декартовы координаты им соответствуют. Определение синуса, косинуса, тангенса и котангенса. Знаки, значения. Формулы, выражающие свойства тригонометрических функций. Связь между тригонометрическими функциями числового и углового аргумента. Таблица значений. Д/з. 1 – 7 № 12,15,16(в, г), 23, 24(а, г), 55.