Презентация на тему: Степень числа с натуральным показателем

Тема урока: Свойства степени с натуральным показателем

«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь» М.В.Ломоносов.

Цели урока: Отработать умения систематизировать, обобщать знания о степени с натуральным показателем, закрепить и усовершенствовать навыки простейших преобразований выражений, содержащих степени с натуральным показателем.

Разминка Если показатель четное число, то значение степени всегда ______________________________ Если показатель нечетное число, то значение степени совпадает со знаком _____________________

Произведение степеней an·ak=an+k При умножении степеней с ________________________ надо основание _____________________________, а показатели степеней ___________________________.

Частное степеней an : ak=an - k При делении степеней с ________________________ надо основание ______________________________, а из показателя делимого ____________________________.

Возведение степени в степень (an)к = ank При возведении степени в степень надо основание _______________________________, а показатели степеней ___________________________.

Если показатель четное число, то значение степени всегда положительное. Если показатель нечетное число, то значение степени совпадает со знаком основания степени.

Произведение степеней an·ak=an+k При умножении степеней с одинаковыми основаниями надо основание оставить тем же, а показатели степеней сложить.

Частное степеней an : ak=an - k При делении степеней с одинаковыми показателями надо основание оставить тем же, а из показателя делимого вычесть показатель делителя.

Возведение степени в степень (an)к = ank При возведении степени в степень надо основание оставить прежним, а показатели степеней перемножить.

Чему равно значение выражения: аm∙аn

аm:an

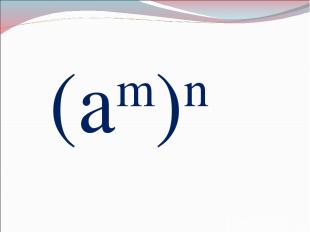
(am)n

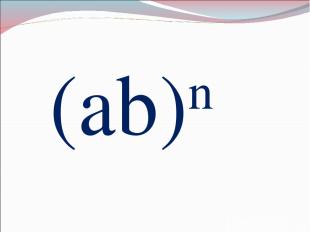
(ab)n

о0

а1

а0

Вычислить а) 2· 62 б) -5· 2 в) 22 ·25

Сравнить числа, не выполняя возведение в степень а) 82 и 83 б) (-5)5 и (-5)2 в)(-1)4 и (-1)6

Записать в виде выражения: Записать в виде выражения: -квадрат суммы х и 3 -разность кубов а и в

Конкурс капитанов Сократить дробь 521+521+521+521+521 ___________________ 524

Блицтурнир Чтобы это значило? а) 45:43=41+?; б) 10?: 105=102; в)( 5?)3 = 512.

Найти значение буквы, при корой равенство будет верно. а) (34)х=38 б) (7t)3=79; в) (5,2a)3=5,212.

Найти значение буквы, при корой равенство будет верно а) (2/3)х=32/243; б) (3/5)х=27/125; в) (3/5)в=9/25.

Найти значение буквы, при корой равенство будет верно а) ((1,3)2)6=1,34х; б) (( 0.1)3)4=0,16х в) (2,4)2=216х.

Найти ошибку: а) (-3)5 0; (-5)3>(-5)2. б) -1,74< 0. х2+у2-квадрат суммы; (-8)8>0. в) –(1/3)2*32=1; (х+у) 3-куб суммы; -192< 0

а) 23*27 =221 ; 23*27 = 410; 23+27=210. в) (2х)3 =2х3; (а3)2 = а9; 310:32 = 35.

Игра «Цепочка» Ответы 1.Представьте в виде степени : 58*25= 2.Упростите: 6n+3: 6n= 3.Сравните: (-1)4 и 17. 4.Вычислите: (217-43,07 *4)0 +5*1/3= 5.Упростите: ((х2)3)5=

ОТВЕТЫ: 510 63=108 (-1)4 = 17 3,5 х30.

102+112+122+132+142 365

Придумать задание по рисунку Х5

Итоги работы Рефлексия Продолжите фразу: Сегодня на уроке …  Теперь я знаю …  Мне на уроке …

– Активно на уроке работали … – Старались …  – Жду большей активности от… – Спасибо всем за работу!