Презентация на тему: Степень с действительным показателем

22 = 32 = 52 = 23 = 33 = 53 = 24 = 34 = 54 = 25 = 35 = 26 = 27 = 112 = 122 = 132 = 142 = 152 = 252 = 16 8 32 64 128 144 121 243 81 27 9 625 225 169 196 625 125 25 4 900igr.net

(a n)m = a n ∙ a m = (ab) n = a n ∙ b n = a n + m a n - m a n m сложить вычесть умножить каждый множитель основания числитель и знаменатель b возвести в степень a n ∙ b n (ab) n Произведение степеней с одинаковыми основаниями Показатели ______________ Частное степеней с одинаковыми основаниями Показатели ______________ Возведение степени в степень Показатели ______________ Возведение произведения в степень Возвести ________ _________________ Произведение степеней с одинаковыми показателями Умножить _______ _________________ Возведение дроби в степень Возвести ________ _________________ Деление степеней с одинаковыми показателями Разделить а на ____ _______________

2. К результату приписать столько нулей, сколько их в основании, умноженном на показатель. 1. Возвести в степень число без нулей; 03 = 8 000 2 02 = 225 00 15 Выполните примеры 20 3 = 150 2 = 400 2 = 360 2 = 110 2 = 12100 129600 160000 22500 8000

2. Справа налево отсчитать столько знаков, сколько их в произведении количества знаков после запятой в основании на показатель степени. 1. Возвести в степень число, не взирая на запятую; 0, 8 0,00 2 2 = 1 21 1,1 Выполните примеры • • • , 3 = • • , Выполните примеры 0,2 3 = 1,1 2 = 0,04 2 = 0,12 2 = 0,15 2 = 0,0225 0,0144 0,0016 1,21 0,008

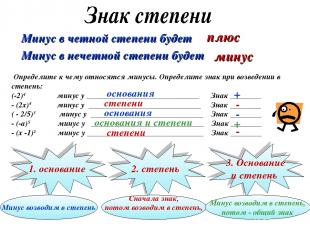
Минус в четной степени будет плюс Минус в нечетной степени будет минус Определите к чему относятся минусы. Определите знак при возведении в степень: (-2)4 минус у _____________________________ Знак ________ - (2х)4 минус у _____________________________ Знак ________ ( - 2/5)3 минус у _____________________________ Знак ________ - (-а)5 минус у _____________________________ Знак ________ - (х -1)2 минус у ______________________________ Знак ________ основания основания степени степени основания и степени Минус возводим в степень Сначала знак, потом возводим в степень, Минус возводим в степень, потом - общий знак - + - - +

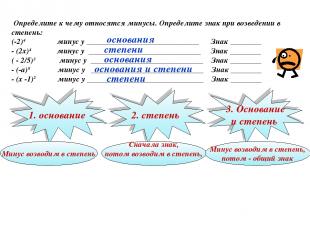
Определите к чему относятся минусы. Определите знак при возведении в степень: (-2)4 минус у _____________________________ Знак ________ - (2х)4 минус у _____________________________ Знак ________ ( - 2/5)3 минус у _____________________________ Знак ________ - (-а)5 минус у _____________________________ Знак ________ - (х -1)2 минус у ______________________________ Знак ________ основания основания степени степени основания и степени Минус возводим в степень Сначала знак, потом возводим в степень, Минус возводим в степень, потом - общий знак

Определите к чему относятся минусы. Определите знак при возведении в степень: (-2)4 минус у _____________________________ Знак ________ - (2х)4 минус у _____________________________ Знак ________ ( - 2/5)3 минус у _____________________________ Знак ________ - (-а)5 минус у _____________________________ Знак ________ - (х -1)2 минус у ______________________________ Знак ________ Выполните примеры. Сначала поставьте знак, потом вычисляйте. (-2)4 = ______________________ - (2х)4 = _______________________ ( - 2/5)3 = _______________________ - (-а)5 = _______________________ основания основания степени степени основания и степени - + - - + + 16 - 16х4 - 8/125 + а5

р – целое число, q – натуральное число, q ≥ 2 Примеры: 2 -1 , 3 ½ , а ¾

(a n)m = a n ∙ a m = (ab) n = a n ∙ b n = a n + m a n - m a n m сложить вычесть умножить каждый множитель основания числитель и знаменатель b возвести в степень a n ∙ b n (ab) n Произведение степеней с одинаковыми основаниями Показатели ______________ Частное степеней с одинаковыми основаниями Показатели ______________ Возведение степени в степень Показатели ______________ Возведение произведения в степень Возвести ________ _________________ Произведение степеней с одинаковыми показателями Умножить _______ _________________ Возведение дроби в степень Возвести ________ _________________ Деление степеней с одинаковыми показателями Разделить а на ____ _______________

Свойства степеней с рациональным показателем такие же как свойства степеней с натуральным показателем а 1/5 · а 2/3 = а 1/5 + 2/3 3 5 = а 13/15 а 1/5 · а -2/3 = а 1/5 - 2/3 3 5 = а -7/15 (5 1/5)15 = а 1/5·15 = 5 3 = 125

Действия с числовыми основаниями 1. Разложение числа на простые множители. Представьте составное числа в виде произведения степеней с простыми основаниями: 1) 12 = _________ 2) 24 = _________ 3) 75 = __________ 4) 48 = ____________ 5) 72 = _________ 6) 250 = _________ 7) 54 = __________ 8) 80 = ____________ Разложите числа на простые множители: 576 864 864 = 576 = 22·3 23·3 52·3 24·3 23·32 53·2 33·2 24·5 2 432 2 216 2 108 2 54 2 27 33 25·33 26·32

2. Определить знак; (можно определять сначала); 1. Возвести в степень при наличии; выполнить действия в числителе и знаменателе; 3. Сократить коэффициенты ; 4. Сократить буквенную часть. 3 1 а 1 3а 2 3 а 1 1 b2 23 1 3 1 x4 1 1 y2

При сокращении дробей числовые основания разложить на множители При сокращении буквенной части – сокращать на букву в меньшей степени Можно не сокращать, а делить степени с одинаковым основанием, т.е. вычитать показатели Десятичную дробь надо перевести в обыкновенную

2. Выполнить действия, используя свойства степеней или арифметические действия и таблицу степеней ; 1. Привести числовые основания к степени с простым основанием; Примеры: 1) 27 х = (3 3)х = 33х 2) 6 х = (2·3 )х = 2 х ·3х Приведение к простому основанию: 3) 0,5 х· 8х = ( ½ )х · 23х = 2х · 23х = 24х 4) 3 х + 9х = 3х + 32х 2 · 2 -2х · 23 = 2 – 2х +4

Примеры: 1) 3 х+1 = 2) 2 х + 2х + 1 + 2х + 2 = Приведение к простому показателю («очищение показателя»): 4) 3 2х - 1 + 3 2х - 2 + 32х - 3= 12 a n + m = a n - m a n ∙ a m 3· 3 х 2х +2· 2х + 4·2х = 7·2х = a - m ∙ a n 1/3 · 32x + 1/9 · 32x + 1/27 · 32x = 33 9 3 1 27 9·32x + 3·32x + 32x = 27·33 13·32x = 27·33 Не умножать! 3 32x = 27·3 = 34