Презентация на тему: Производная степенной функции

Производная степенной функции Prezented.Ru

Математики о производной. « Слова «производная» и «произошло» имеют похожие части слова, да и смысл похож: производная происходит от исходной функции (переложив на отношения человека: исходная функция - «мама», её производная - «дочь»). Производная - часть математической науки, одно из её звеньев. Нет этого звена - прерваны связи между многими понятиями.»

Что называется производной? Производной функции в данной точке называется предел отношения приращения функции в этой точке к приращению аргумента, когда приращение аргумента стремится к нулю.

«Алгоритм нахождения производной»

Исследуя функции, можно встретить случаи, когда функция определена, но не дифференцируема. Что это? Почему так происходит? Можно ли этому найти объяснения?

Взгляд из детства. Всем с детства известно такое явление, как движение мяча, падающего на пол и упруго отскакивающего от него. Это явление можно объяснить с помощью законов физики. Попробуем переложить всё это на математический язык.

При отскоке от пола (при h=0) направление движения мяча меняется (и функция достигает минимума), однако в эти моменты скорость мяча не равна нулю, касательную к графику h провести нельзя. На графике скорости мяча мы видим: в момент отскока скорость мяча однозначно найти нельзя - график скорости в эти моменты имеет разрывы. (Производная в этих точках не существует).

Примеры функций, имеющих особые точки. Все функции вида у = |f(x)|, при f(x)=0 имеют особые точки - точки излома. Частный случай: у = |х|, где х=0 - особая точка.

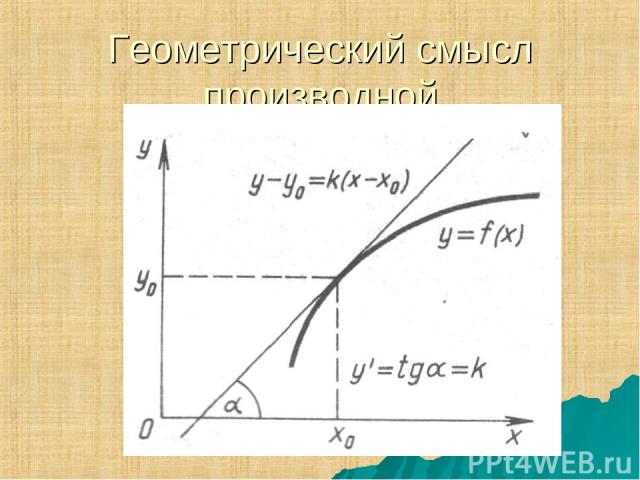
Геометрический смысл производной состоит в том, что значение производной функции y=f(x) в точке x равно угловому коэффициенту касательной к графику функции в точке с абсциссой x0
Геометрический смысл производной

Физический смысл скорость ускорение Производная от перемещения по времени является мгновенная скорость. Производная от скорости по времени является ускорением.

Точка движется прямолинейно по закону Вычислите скорость движения точки: а) в момент времени t; б) в момент времени t=2с. Решение. а) б)

Найдите скорость и ускорение для точки, движущейся по закону а) в момент времени t; б) в момент времени t=3с. Решение.

Проблемная задача Две материальные точки движутся прямолинейно по законам В какой момент времени скорости их равны, т.е.

Решение проблемной задачи

Разбор некоторых задач самостоятельной работы m(l) = 3l2 + 5l (г), lАВ = 20 см, сер= ? Решение: Т.к. (l) = m′(l), то (l) = 6l + 5. l = 10 см, (10) = 60 + 5 = 65(г/см3) Ответ: 65 г/см3.

Разбор некоторых задач самостоятельной работы