Презентация на тему: Преобразование Фурье

Преобразование Фурье

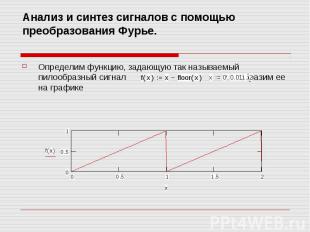
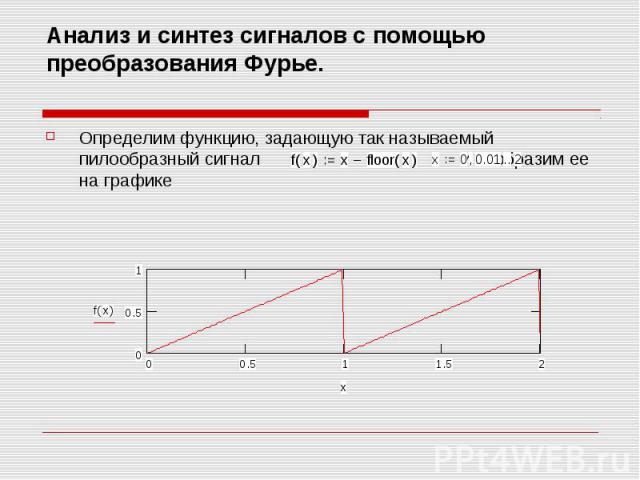
Анализ и синтез сигналов с помощью преобразования Фурье. Определим функцию, задающую так называемый пилообразный сигнал и изобразим ее на графике

Заполним массив s: Проводим прямое преобразование Фурье: Внимание! В том случае, когда в массиве s содержится элементов, причем все числа действительные, следует использовать функцию fft. Во всех остальных случаях – функцию cfft. Массив g содержит комплексные коэффициенты дискретного преобразования Фурье. Размер массива f –

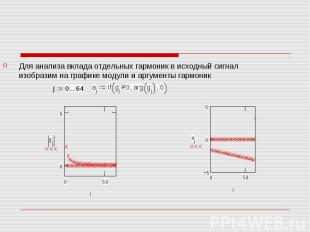
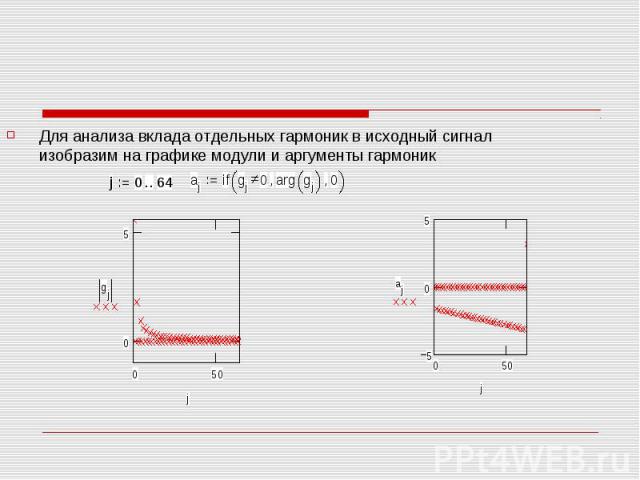
Для анализа вклада отдельных гармоник в исходный сигнал изобразим на графике модули и аргументы гармоник Для анализа вклада отдельных гармоник в исходный сигнал изобразим на графике модули и аргументы гармоник

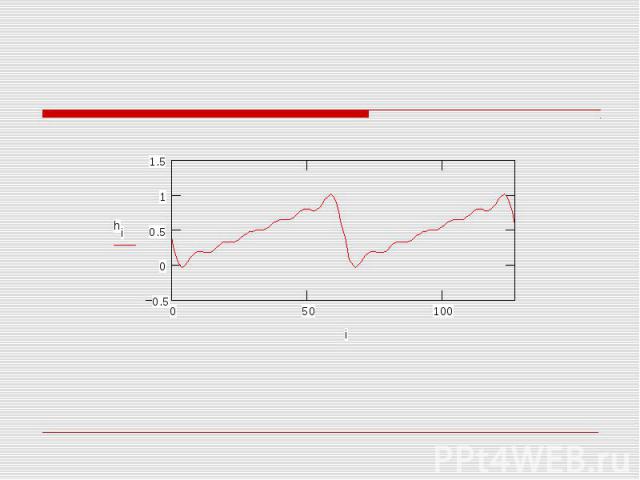
Проводим обратное преобразование Фурье, исключив гармоники с малым вкладом. Будем учитывать только гармоники с амплитудой не менее 0.3. Для отсечения слагаемых с малым вкладом воспользуемся функцией единичного скачка – функцией Хевисайда Ф. Для обратного преобразования Фурье используется функция ifft, если прямое преобразование осуществлялось с помощью fft, и cifft, если прямое преобразование осуществлялось с помощью cfft.

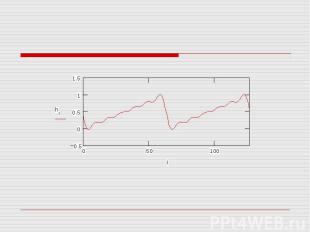
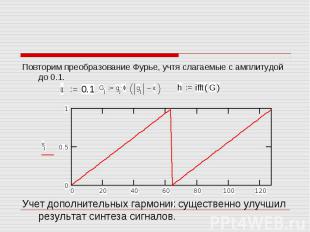
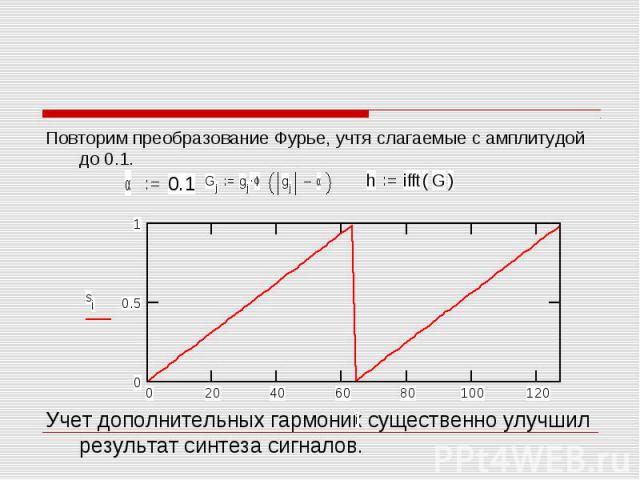
Повторим преобразование Фурье, учтя слагаемые с амплитудой до 0.1. Учет дополнительных гармоник существенно улучшил результат синтеза сигналов.

Наилучшее приближение