Презентация на тему: Функция y = ax².

Функция y=ax2. Её график и свойства. 9 класс Составила: Икрянова А.С.

Сегодня на уроке: введем понятие квадратичной функции научимся строить график функции y=ax2 изучим свойства функции y=ax2

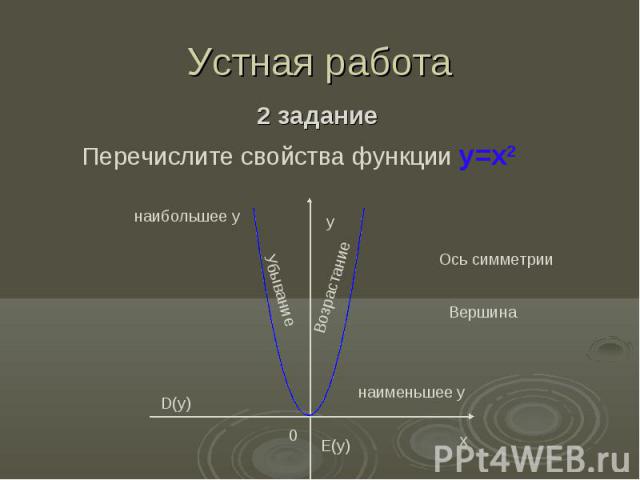
Устная работа
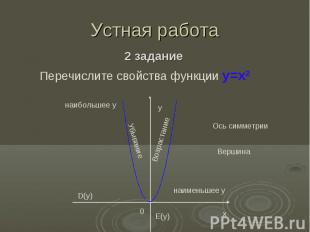
Устная работа
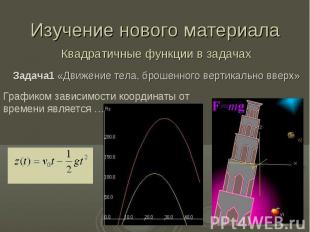
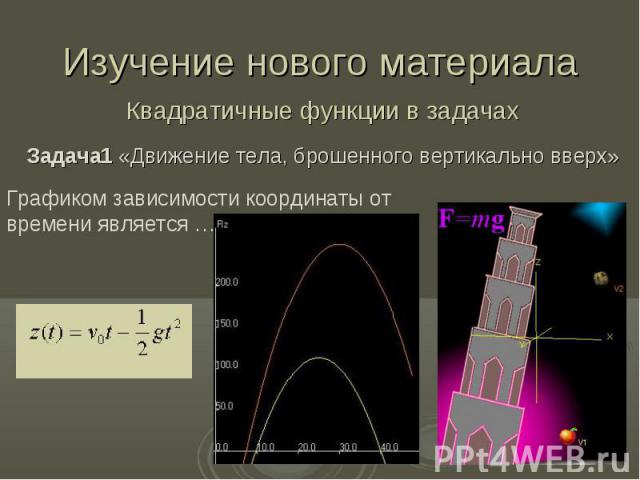
Изучение нового материала Квадратичные функции в задачах Задача1 «Движение тела, брошенного вертикально вверх»

Выразим площадь дна коробки (х – глубина коробки) Выразим площадь дна коробки (х – глубина коробки)

Примем боковую сторону куба за а Примем боковую сторону куба за а

Квадратичная функция y=ax2+bx+c a, b, c – некоторые числа a = 0, x – независимая переменная
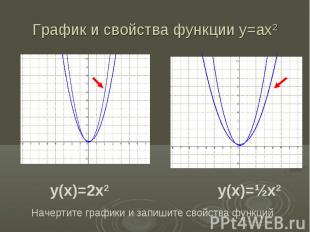
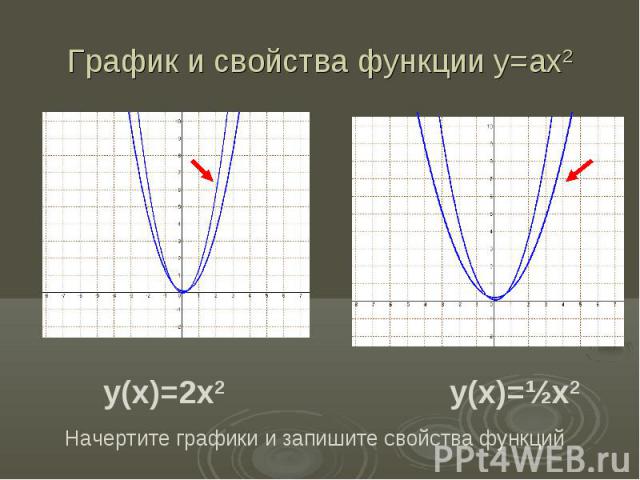
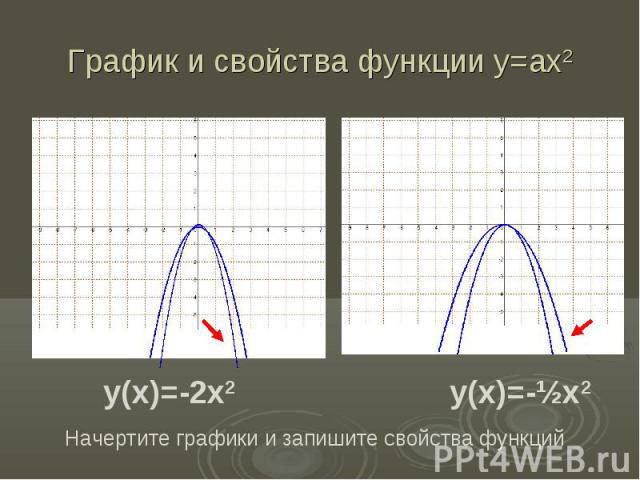
График и свойства функции у=ах2
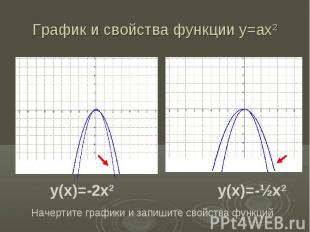
График и свойства функции у=ах2

Тренировочные упражнения № 90 – на доске и в тетрадях (на миллиметровой бумаге) № 94 – самостоятельно с последующей проверкой № 97 – устно

Закрепим изученное: «Вопрос – ответ»

Что произойдёт с графиком функции у=х2, если функция изменится на у=-3х2?

Какую функцию называют квадратичной?

Назовите область значения функции у=-5х2

ОЦЕНКА «5»

Что произойдёт с графиком функции у=х2, если функция изменится на у=3,5х2?

Назовите промежутки возрастания и убывания функции у=ах2, если -1<а<0

Какое значение параметра а должно быть, чтобы функция у=ах2 не имела наибольшего значения?

Будет ли прямая у=9 пресекать график функции у=-3х2? Ответ обоснуйте.

Как называется точка пересечения параболы с её осью симметрии?

Домашнее задание п.5 (стр.28) №№ 91, 92, 96 (устно), 103 заполнить таблицу