Презентация на тему: Линейная и квадратичная функции

Функции: линейная, обратная пропорциональность, квадратичная Справочный материал для учащихся Составила: учитель математики Косова В.И. МБОУ гимназия № 9 г. Ставрополь 900igr.net

Линейная функция Линейной функцией называется функция, которую можно задать формулой вида y=kx+b, де x-независимая переменная,k и b-некоторые числа. Графиком линейной функции является прямая. у Угловой коэффициент k= tg b – ордината точки пересечения графика b с осью Оу х
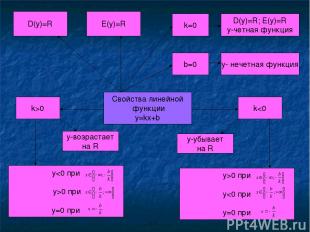
Свойства линейной функции y=kx+b D(y)=R E(y)=R k=0 b=0 D(y)=R; E(y)=R y-четная функция y- нечетная функция k>0 k0 при y

Частные случаи линейной функции Прямая пропорциональность y = kx у k х 1 Постоянная функция y = b у b х

Взаимное расположение графиков линейных функций Если k1=k2, графики функций y = k1x+b1 и y= k2x+b2 пересе- каются в одной точке у х Если k1=k2, графики функций y = k1x+b1 и y = k2x+b2 являют- ся параллельными прямыми (при различных b1 и b2) у х

Построение графика линейной функции y=kx+b с помощью элементарных преобразований графика функции y=x 1.Построить график 2. Произвести растяжение 3. Произвести парал- функции y=x (при /k/ >1) или сжатие лельный перенос гра- (при /k/

Обратная пропорциональность Обратной пропорциональностью называется функция, которую можно задать формулой вида где x – независимая переменная, k – не равное нулю число Кривую, являющуюся графиком обратной пропорциональности, называют гиперболой При k>0 график функции расположен в первой и третьей координатных четвертях, при k

Свойства функции у-нечетная функция k>0 k0 при x

Квадратичная функция Квадратичной называется функция, которую можно задать формулой вида у=ах2+вх+с, где х- независимая переменная а,в,с- некоторые числа, причем а 0 Графиком квадратичной функции является парабола Свойства функции и вид ее графика определяются, в основном, значениями коэффициента а и дискриминанта уравнения ах2+вх+с=0

График квадратичной функции a>0, D>0 a>0, D=0 a>0, D

Свойства квадратичной функции у=ах2+вх+с D(y)=R E(y): при а>0 ; при а0 : функция возрастает на функция убывает на При а























