Презентация на тему: Кривые второго порядка

§ Кривые второго порядка Кривые второго порядка делятся на 1) вырожденные и 2) невырожденные Вырожденные кривые второго порядка это прямые и точки, которые задаются уравнением второй степени. Если уравнению второго порядка не удовлетворяет ни одна точка плоскости, то тоже говорят, что уравнение определяет вырожденную кривую (мнимую кривую второго порядка). Невырожденными кривыми второго порядка являются эллипс, окружность, гипербола и парабола. 900igr.net

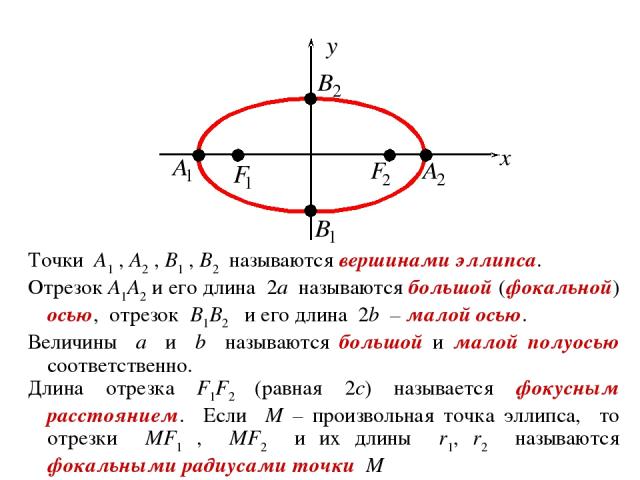
1. Эллипс и окружность ОПРЕДЕЛЕНИЕ. Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух фиксированных точек плоскости F1 и F2 есть величина постоянная и равная 2a (2a>|F1F2|). Точки F1 и F2 называют фокусами эллипса. Выберем декартову прямоугольную систему координат так, чтобы фокусы F1 и F2 лежали на оси Ox на одинаковом расстоянии от O. В такой системе координат: F1(–c;0) и F2(c;0) , где |OF1| = |OF2| = c.

Уравнение (1): называется каноническим уравнением эллипса. Система координат, в которой эллипс имеет такое уравнение, называется его канонической системой координат.

СВОЙСТВА ЭЛЛИПСА 1) Эллипс лежит внутри прямоугольника, ограниченного x= a, y= b. 2) Эллипс имеет центр симметрии (начало координат) и две оси симметрии (оси Ox и Oy). Центр симметрии эллипса называют центром эллипса. Ось симметрии эллипса, проходящую через фокусы (ось Ox) называют большой (или фокальной) осью симметрии, а вторую ось (ось Oy) – малой осью. 3) Из уравнения эллипса получаем:

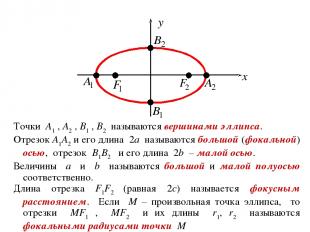
Точки A1 , A2 , B1 , B2 называются вершинами эллипса. Отрезок A1A2 и его длина 2a называются большой (фокальной) осью, отрезок B1B2 и его длина 2b – малой осью. Величины a и b называются большой и малой полуосью соответственно. Длина отрезка F1F2 (равная 2c) называется фокусным расстоянием. Если M – произвольная точка эллипса, то отрезки MF1 , MF2 и их длины r1, r2 называются фокальными радиусами точки M

ОПРЕДЕЛЕНИЕ. Величина , равная отношению фокусного расстояния эллипса к его большой оси, называется эксцентриситетом эллипса, т.е. Величина характеризует форму эллипса. Зная эксцентриситет эллипса легко найти фокальные радиусы точки M(x;y): Замечания. 1) Пусть в уравнении эллипса a = b = r. Для этой кривой Геометрически, это означает, что точки кривой равноудалены (на расстояние r) от ее центра O, т.е. кривая является окружностью. Каноническое уравнение окружности принято записывать в виде x2 + y2 = r2 , где r – расстояние от любой точки окружности до ее центра; r называют радиусом окружности.

2) Если выбрать систему координат так, чтобы фокусы F1 и F2 были на оси Oy на одинаковом расстоянии от начала координат, то уравнение эллипса будет иметь вид Для этого эллипса большая ось – ось Oy, малая ось – ось Ox, фокусы имеют координаты F1(0;–c) и F2(0;c) , где Фокальные радиусы точки M(x;y) находятся по формулам

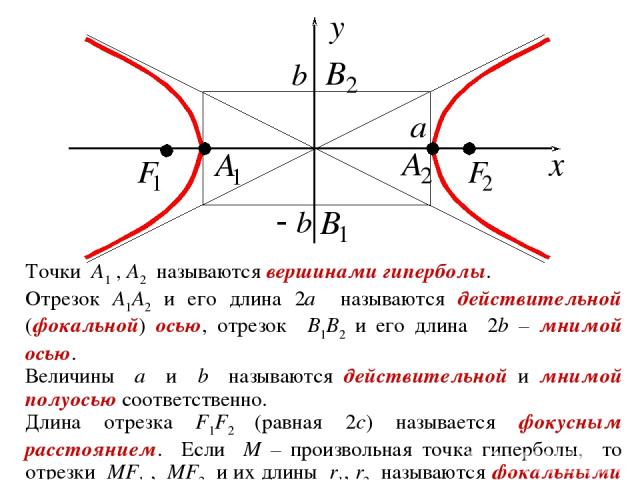
2. Гипербола ОПРЕДЕЛЕНИЕ. Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от которых до двух фиксированных точек плоскости F1 и F2 есть величина постоянная и равная 2a (2a < |F1F2|). Точки F1 и F2 называют фокусами гиперболы. Выберем декартову прямоугольную систему координат так, чтобы фокусы F1 и F2 лежали на оси Ox на одинаковом расстоянии от O. В такой системе координат: F1(–c;0) и F2(c;0) , где |OF1| = |OF2| = c.

Уравнение (2): называется каноническим уравнением гиперболы. Система координат, в которой гипербола имеет такое уравнение, называется ее канонической системой координат.

СВОЙСТВА ГИПЕРБОЛЫ 1) Точек гиперболы нет в полосе, ограниченной прямыми x= a. 2) Гипербола имеет центр симметрии (начало координат) и две оси симметрии (оси Ox и Oy). Центр симметрии гиперболы называют центром гиперболы. Ось симметрии гиперболы, проходящую через фокусы (ось Ox) называют действительной (или фокальной) осью симметрии, а вторую ось (ось Oy) – мнимой осью. 3) Из уравнения гиперболы получаем:

Прямая ℓ называется асимптотой кривой, если расстояние от точки M кривой до прямой ℓ стремится к нулю при удалении точки M от начала координат. Существуют два вида асимптот – вертикальные и наклонные. Вертикальные асимптоты кривая y=f(x) имеет в тех точках разрыва II рода функции y=f(x) , в которых хотя бы один из односторонних пределов функции равен бесконечности. Наклонные асимптоты кривой y=f(x) имеют уравнение y=k1,2x+b1,2 , где

Точки A1 , A2 называются вершинами гиперболы. Отрезок A1A2 и его длина 2a называются действительной (фокальной) осью, отрезок B1B2 и его длина 2b – мнимой осью. Величины a и b называются действительной и мнимой полуосью соответственно. Длина отрезка F1F2 (равная 2c) называется фокусным расстоянием. Если M – произвольная точка гиперболы, то отрезки MF1 , MF2 и их длины r1, r2 называются фокальными радиусами точки M

ОПРЕДЕЛЕНИЕ. Величина , равная отношению фокусного расстояния гиперболы к ее действительной оси, называется эксцентриситетом гиперболы, т.е. Величина характеризует форму гиперболы. Зная эксцентриситет гиперболы легко найти фокальные радиусы точки M(x;y). Если точка M лежит на правой ветке гиперболы (т.е. x > 0), то Если M лежит на левой ветке гиперболы (т.е. x < 0), то

Замечания. 1) Если в уравнении гиперболы a=b, то гипербола называется равнобочной. Асимптоты равнобочной гиперболы, перпендикулярны. можно выбрать систему координат так, чтобы координатные оси совпали с асимптотами. Тогда уравнение гиперболы будет xy=0,5a2 . (3) Уравнение (3) называют уравнением равнобочной гипер- болы, отнесенной к асимптотам.

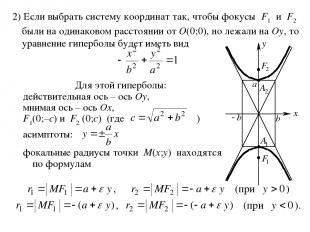
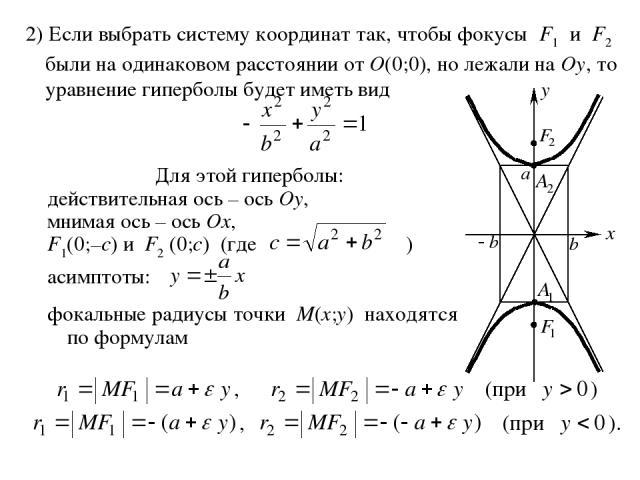
2) Если выбрать систему координат так, чтобы фокусы F1 и F2 были на одинаковом расстоянии от O(0;0), но лежали на Oy, то уравнение гиперболы будет иметь вид Для этой гиперболы: действительная ось – ось Oy, мнимая ось – ось Ox, F1(0;–c) и F2 (0;c) (где ) асимптоты: фокальные радиусы точки M(x;y) находятся по формулам

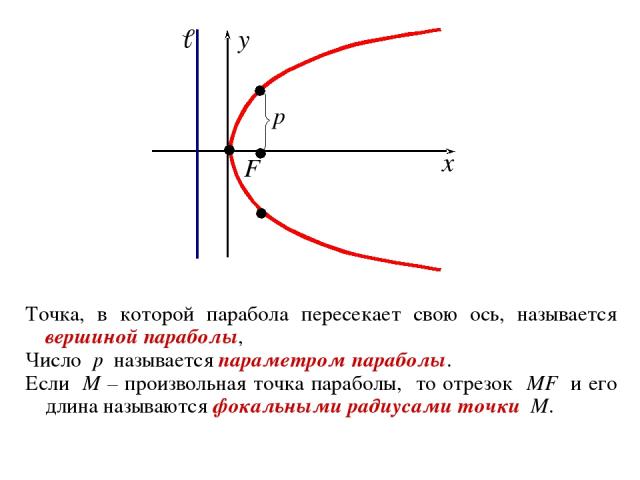
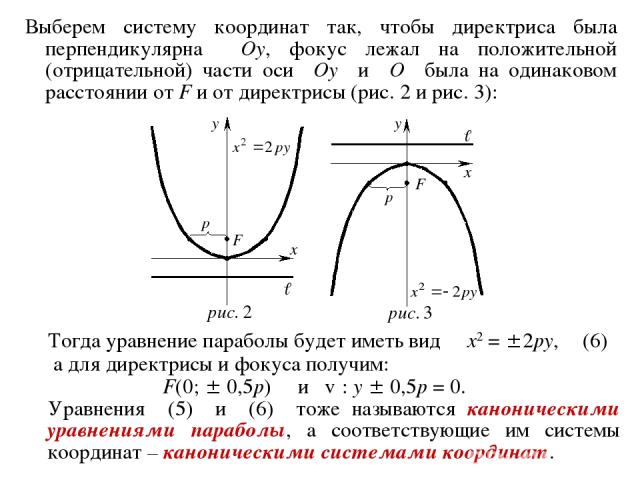
3. Парабола Пусть ℓ – некоторая прямая на плоскости, F – некоторая точка плоскости, не лежащая на прямой ℓ. ОПРЕДЕЛЕНИЕ. Параболой называется геометрическое место точек плоскости, расстояние от которых до фиксированной прямой ℓ и до фиксированной точки F (не лежащей на прямой ℓ) одинаково. Точку F называют фокусом параболы, прямую ℓ – директрисой. Выберем декартову прямоугольную систему координат так, директриса параболы ℓ была перпендикулярна оси Ox, фокус F лежал на положительной части Ox и расстояние от O до F и до ℓ было одинаковым. В такой системе координат: F (0,5p;0) и ℓ: x + 0,5p =0 , где p – расстояние от F до ℓ .

Уравнение (4): y2 = 2px называется каноническим уравнением параболы. Система координат, в которой парабола имеет такое уравнение, называется ее канонической системой координат.

СВОЙСТВА ПАРАБОЛЫ 1) Парабола лежит в полуплоскости x ≥ 0. 2) Парабола имеет ось симметрии (ось Ox). Ось симметрии параболы называют осью параболы. 3) Из уравнения параболы получаем:

СВОЙСТВА ПАРАБОЛЫ 1) Парабола лежит в полуплоскости x ≥ 0. 2) Парабола имеет ось симметрии (ось Ox). Ось симметрии параболы называют осью параболы. 3) Из уравнения параболы получаем:

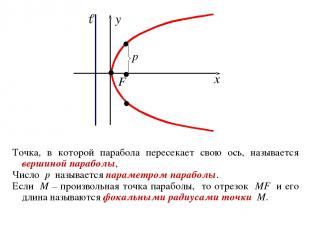
Точка, в которой парабола пересекает свою ось, называется вершиной параболы, Число p называется параметром параболы. Если M – произвольная точка параболы, то отрезок MF и его длина называются фокальными радиусами точки M.

Замечание. Введем систему координат так, чтобы фокус F параболы лежал на отрицательной части оси Ox, директриса была перпендикулярна Ox, и расстояние от O до F и до директрисы было одинаково. Тогда получим для параболы уравнение y2 = –2px, (5) а для директрисы и фокуса: F(–0,5p;0) и ℓ : x – 0,5p = 0.

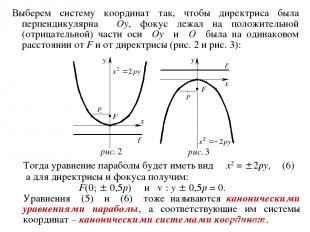
Выберем систему координат так, чтобы директриса была перпендикулярна Oy, фокус лежал на положительной (отрицательной) части оси Oy и O была на одинаковом расстоянии от F и от директрисы (рис. 2 и рис. 3): Тогда уравнение параболы будет иметь вид x2 = 2py, (6) а для директрисы и фокуса получим: F(0; 0,5p) и ℓ : y 0,5p = 0. Уравнения (5) и (6) тоже называются каноническими уравнениями параболы, а соответствующие им системы координат – каноническими системами координат.

4. Координаты точки в разных системах координат Получаем: Формулу (8) называют формулой преобразования координат точки при переносе начала координат в точку C(x0;y0).

5. Общее уравнение кривой второго порядка Рассмотрим уравнение Ax2 + Cy2 + 2Dx + 2Ey + F = 0 (13) С помощью элементарных преобразований, уравнение (13) может быть приведено к виду: ВЫВОД: Уравнение (13) определяет кривую, каноническая система координат которой параллельна заданной, но имеет начало в точке C(x0,y0). Говорят: уравнение (13) определяет кривую со смещенным центром (вершиной), а уравнение (14) называют каноническим уравнением кривой со смещенным центром (вершиной).

Замечание. Приводить уравнение (13) к виду (14) необходимо, если мы хотим построить кривую. Тип кривой можно определить и без уравнения (14). А именно: 1) если AC = 0, то кривая является параболой; 2) если AC < 0, то кривая является гиперболой; 3) если AC > 0, A ≠ C– эллипсом; 4) если AC > 0, A = C – окружностью.

6. Общее определение эллипса, гиперболы и параболы Пусть M – произвольная точка эллипса или гиперболы. ri = | MFi | , di = d(M,ℓi) ТЕОРЕМА. Для любой точки M эллипса (гиперболы) имеет место равенство ЗАМЕЧАНИЕ. По определению параболы r = d. параболу можно считать кривой, у которой эксцентриситет = 1. ОПРЕДЕЛЕНИЕ. Геометрическое место точек, для которых отношение расстояния до фиксированной точки (фокуса) к расстоянию до фиксированной прямой (директрисы) есть величина постоянная и равная , называется 1) эллипсом, если 1; 3) параболой, если = 1.

7. Оптическое свойство эллипса, гиперболы и параболы Получаем: α = β .С физической точки зрения это означает: 1) Если источник света находится в одном из фокусов эллиптического зеркала, то лучи его, отразившись от зеркала, собираются в другом фокусе. 2) Если источник света находится в одном из фокусов гиперболического зеркала, то лучи его, отразившись от зеркала, идут далее так, как если бы они исходили из другого фокуса. 3) Если источник света находится в фокусе параболического зеркала, то лучи его, отразившись от зеркала, идут далее параллельно оси.

§ Поверхности второго порядка Поверхностью второго порядка называется геометрическое место точек в пространстве, декартовы координаты которых удовлетворяют уравнению F(x,y,z) = 0, где F(x,y,z) – многочлен степени 2. в общем случае уравнение поверхности 2-го порядка имеет вид: a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+2a10x+2a20y+2a30z+a00=0 . Поверхности второго порядка делятся на 1) вырожденные и 2) невырожденные Вырожденные поверхности второго порядка это плоскости и точки, которые задаются уравнением второй степени. Если уравнению второго порядка не удовлетворяет ни одна точка пространства, то тоже говорят, что уравнение определяет вырожденную поверхность (мнимую поверхность второго порядка). Невырожденными поверхности второго порядка подразделяются на пять типов.

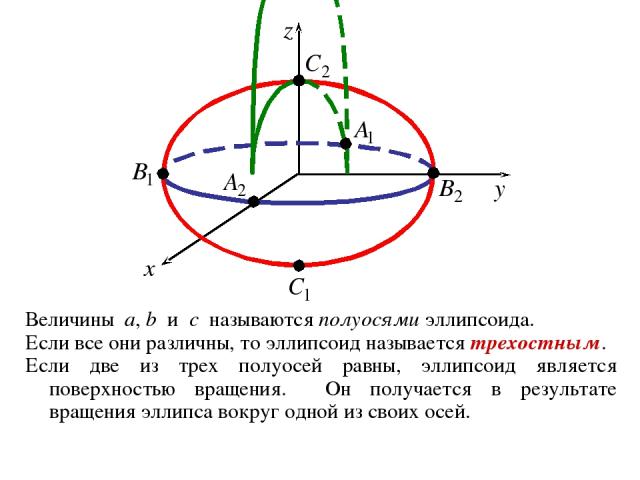
1. Эллипсоид ОПРЕДЕЛЕНИЕ. Эллипсоидом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе координат удовлетворяют уравнению где a, b, c – положительные константы. Система координат, в которой эллипсоид имеет уравнение (1) называется его канонической системой координат, а уравнение (1) – каноническим уравнением эллипсоида.

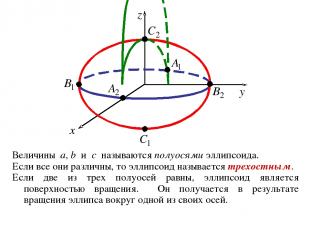
Величины a, b и c называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехостным. Если две из трех полуосей равны, эллипсоид является поверхностью вращения. Он получается в результате вращения эллипса вокруг одной из своих осей.

Эллипсоид, у которого все три полуоси равны, называют сферой. Каноническое уравнение сферы принято записывать в виде x2 + y2 + z2 = r2, где r – величина полуосей, которая называется радиусом сферы. С геометрической точки зрения, сфера – геометрическое место точек пространства, равноудаленных (на расстояние r) от некоторой фиксированной точки (называемой центром). В канонической системе координат сферы, центр – начало координат.

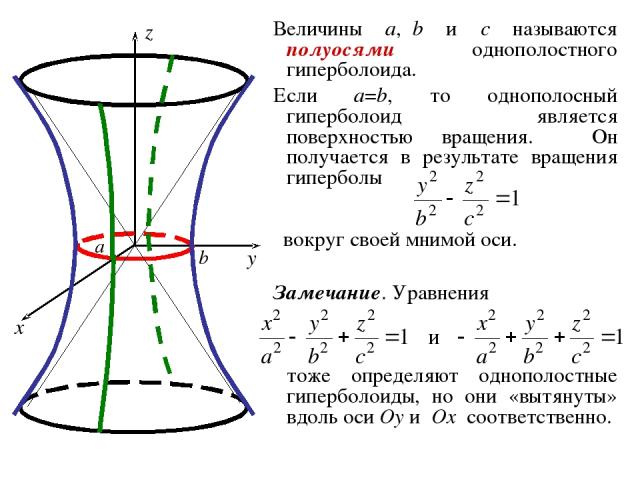
2. Гиперболоиды ОПРЕДЕЛЕНИЕ. Однополостным гиперболоидом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе координат удовлетворяют уравнению где a, b, c – положительные константы. Система координат, в которой однополостный гиперболоид имеет уравнение (2) называется его канонической системой координат, а уравнение (2) – каноническим уравнением однополостного гиперболоида.

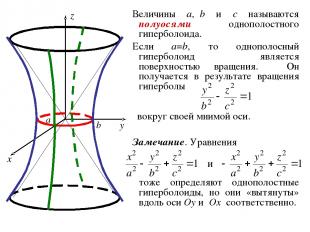
Величины a, b и c называются полуосями однополостного гиперболоида. Если a=b, то однополосный гиперболоид является поверхностью вращения. Он получается в результате вращения гиперболы вокруг своей мнимой оси. тоже определяют однополостные гиперболоиды, но они «вытянуты» вдоль оси Oy и Ox соответственно. Замечание. Уравнения

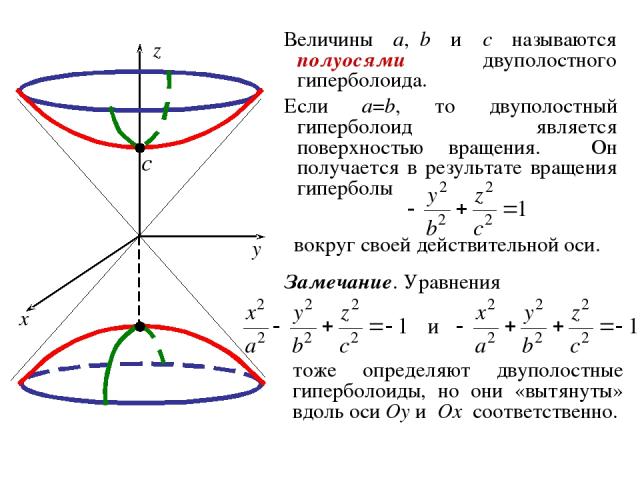
ОПРЕДЕЛЕНИЕ. Двуполостным гиперболоидом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе координат удовлетворяют уравнению где a, b, c – положительные константы. Система координат, в которой двуполостный гиперболоид имеет уравнение (3) называется его канонической системой координат, а уравнение (3) – каноническим уравнением двуполостного гиперболоида.

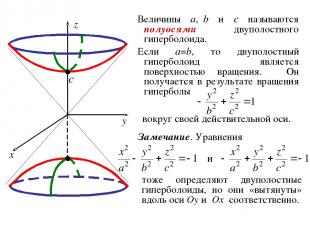
Величины a, b и c называются полуосями двуполостного гиперболоида. Если a=b, то двуполостный гиперболоид является поверхностью вращения. Он получается в результате вращения гиперболы вокруг своей действительной оси. тоже определяют двуполостные гиперболоиды, но они «вытянуты» вдоль оси Oy и Ox соответственно. Замечание. Уравнения

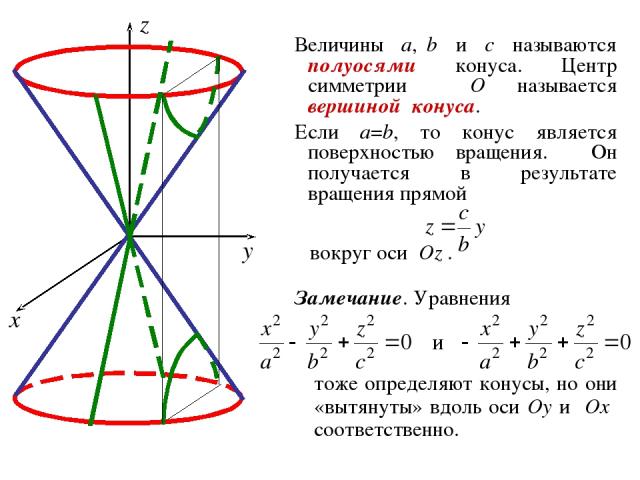
3. Конус ОПРЕДЕЛЕНИЕ. Конусом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе координат удовлетворяют уравнению где a, b, c – положительные константы. Система координат, в которой конус имеет уравнение (4) называется его канонической системой координат, а уравнение (4) – каноническим уравнением конуса.

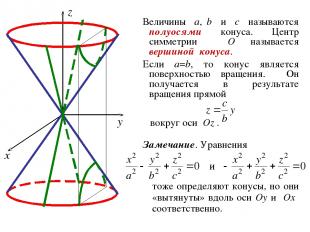
Величины a, b и c называются полуосями конуса. Центр симметрии O называется вершиной конуса. Если a=b, то конус является поверхностью вращения. Он получается в результате вращения прямой вокруг оси Oz . Замечание. Уравнения тоже определяют конусы, но они «вытянуты» вдоль оси Oy и Ox соответственно.

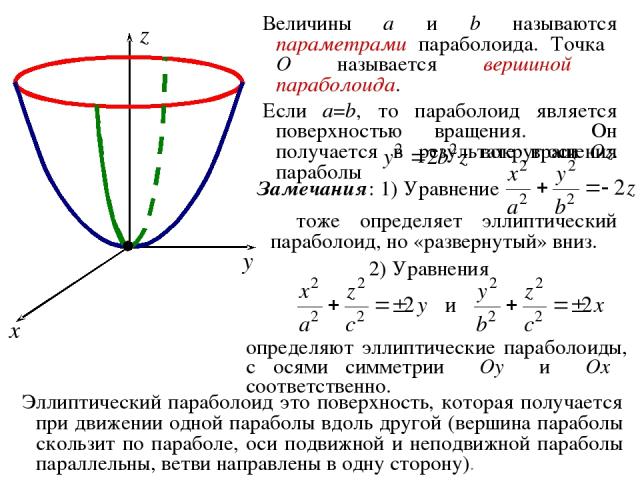
4. Параболоиды ОПРЕДЕЛЕНИЕ. Эллиптическим параболоидом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе координат удовлетворяют уравнению где a, b – положительные константы. Система координат, в которой эллиптический параболоид имеет уравнение (5) называется его канонической системой координат, а уравнение (5) – каноническим уравнением эллиптического параболоида.

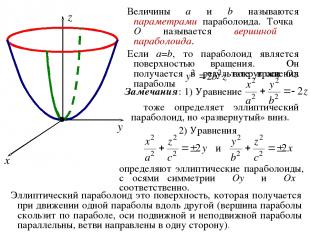
Величины a и b называются параметрами параболоида. Точка O называется вершиной параболоида. Если a=b, то параболоид является поверхностью вращения. Он получается в результате вращения параболы вокруг оси Oz. Эллиптический параболоид это поверхность, которая получается при движении одной параболы вдоль другой (вершина параболы скользит по параболе, оси подвижной и неподвижной параболы параллельны, ветви направлены в одну сторону). Замечания: 1) Уравнение тоже определяет эллиптический параболоид, но «развернутый» вниз. 2) Уравнения определяют эллиптические параболоиды, с осями симметрии Oy и Ox соответственно.

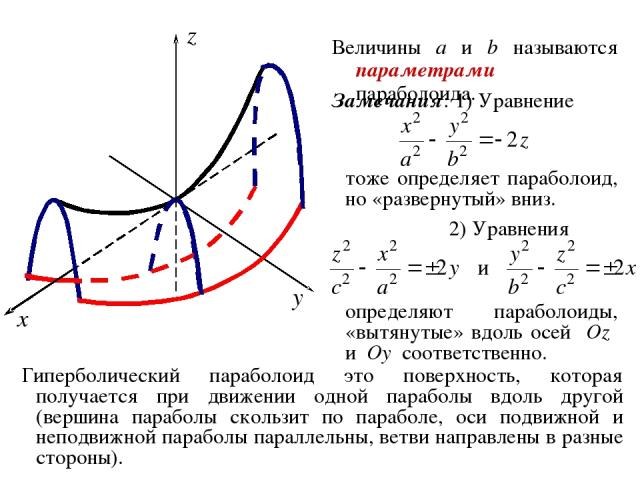
ОПРЕДЕЛЕНИЕ. Гиперболическим параболоидом называется геометрическое место точек пространства, координаты которых в некоторой декартовой системе координат удовлетворяют уравнению где a, b – положительные константы. Система координат, в которой гиперболический параболоид имеет уравнение (6) называется его канонической системой координат, а уравнение (6) – каноническим уравнением гиперболического параболоида.

Величины a и b называются параметрами параболоида. Замечания: 1) Уравнение тоже определяет параболоид, но «развернутый» вниз. 2) Уравнения определяют параболоиды, «вытянутые» вдоль осей Oz и Oy соответственно. Гиперболический параболоид это поверхность, которая получается при движении одной параболы вдоль другой (вершина параболы скользит по параболе, оси подвижной и неподвижной параболы параллельны, ветви направлены в разные стороны).

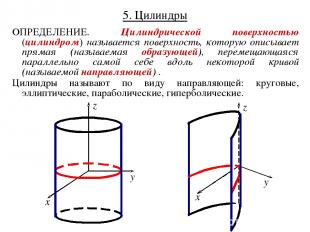
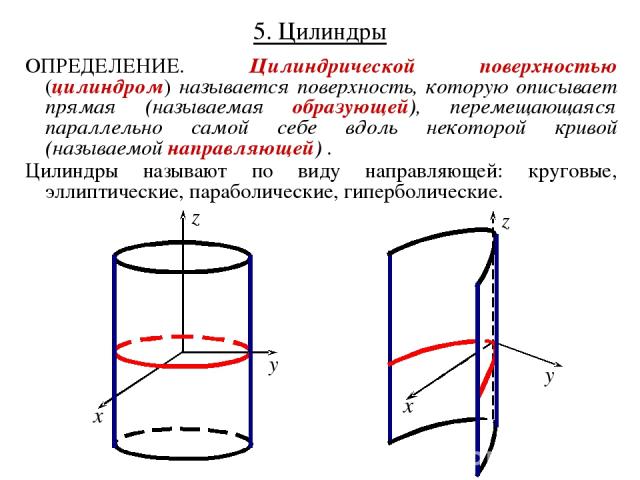
5. Цилиндры ОПРЕДЕЛЕНИЕ. Цилиндрической поверхностью (цилиндром) называется поверхность, которую описывает прямая (называемая образующей), перемещающаяся параллельно самой себе вдоль некоторой кривой (называемой направляющей) . Цилиндры называют по виду направляющей: круговые, эллиптические, параболические, гиперболические.

Цилиндр в некоторой декартовой системе координат задается уравнением, в которое не входит одна из координат. Кривая, которую определяет это уравнение в соответствующей координатной плоскости, является направляющей цилиндра; а образующая – параллельна оси отсутствующей координаты.