Презентация на тему: Технология деятельностного метода как необходимое условие современного урока в начальной школе

Технология деятельностного метода как необходимое условие современного урока в начальной школе

С.И.Ожегов Деятельность – занятия, труд (научная д., педагогическая д.) Л.Г.Петерсон Учебная деятельность – это деятельность ученика, связанная, с одной стороны, с освоением культурных ценностей общества, а с другой – с формированием способностей к самоизменению и рефлексии, обеспечивающих адекватное самоопределение и успешную самореализацию человека в жизни.

Качество образования – это степень соответствия его результатов социальному заказу, отраженному в нормативно закрепленных целях образования (Законе об образовании, перспективных планах и т.д.) Качество продута деятельности – это степень соответствия свойств данного продукта поставленной в деятельности цели. Каковы приоритетные цели современного образования?

А. Дистервег «Главная цель воспитателя должна заключаться в развитии самодеятельности, благодаря которой человек может впоследствии стать распорядителем своей судьбы, продолжателем образования своей жизни…». К.Д. Ушинский «Дать труд человеку, труд свободный, наполняющий душу, и дать средства к выполнению этого труда – вот полное определение цели педагогической деятельности».

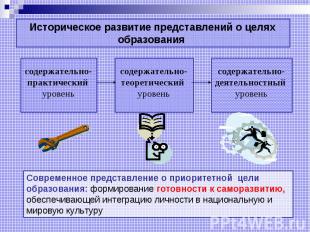
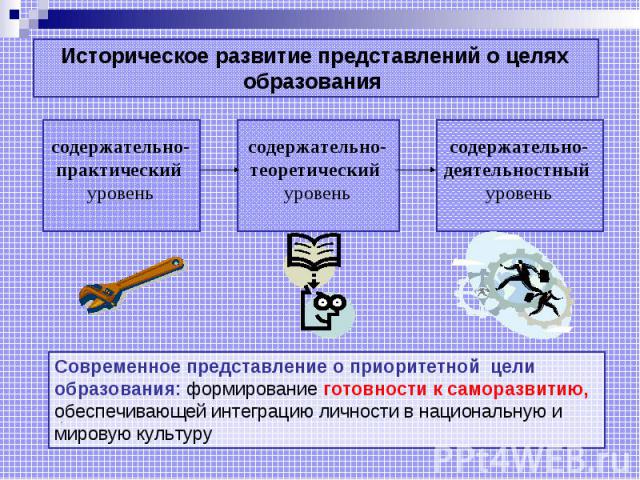
Историческое развитие представлений о целях образования содержательно-практический уровень содержательно-теоретический уровень содержательно-деятельностный уровень Современное представление о приоритетной цели образования: формирование готовности к саморазвитию, обеспечивающей интеграцию личности в национальную и мировую культуру

Умение самостоятельно делать выбор, адекватный своим способностям Умение ставить перед собой цель, принимать решение Умение самостоятельно находить выход в нестандартной ситуации Умение проконтролировать себя, свои собственные действия Умение адекватно оценить свои действия, выявить и скорректировать возникшие затруднения Умение согласовывать свою позицию с другими людьми, общаться

Закон РФ «Об образовании», ст. 14 «Содержание образования является одним из факторов экономического и социального прогресса общества и должно быть ориентировано на обеспечение самоопределения личности, создание условий для ее самореализации ...» «О приоритетных направлениях развития образования в Российской Федерации» «Формируются современные представления о фундаментальности образования – это такое образование, благодаря которому человек способен самостоятельно работать, учиться и переучиваться». Как? Каким способом?

Сократ «Человек не может научиться играть на флейте, не приставив ее к губам». Древняя китайская пословица «Скажи мне – и я забуду. Покажи мне – и я запомню. Вовлеки меня – и я научусь».

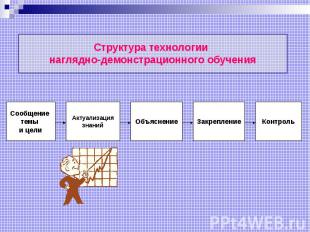
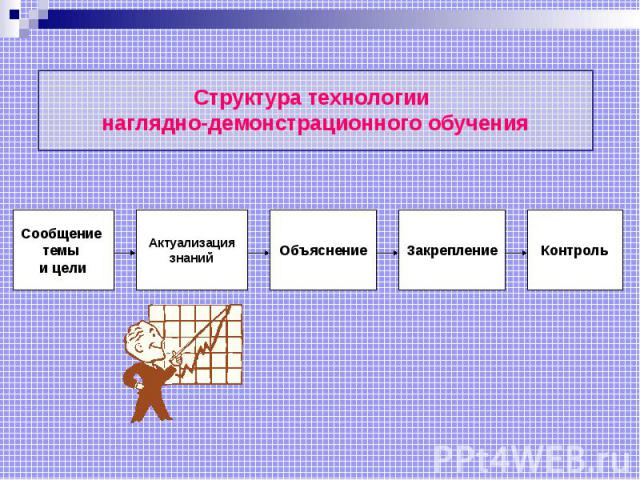
Структура технологии наглядно-демонстрационного обучения

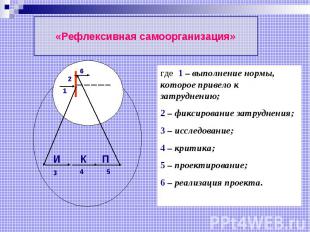
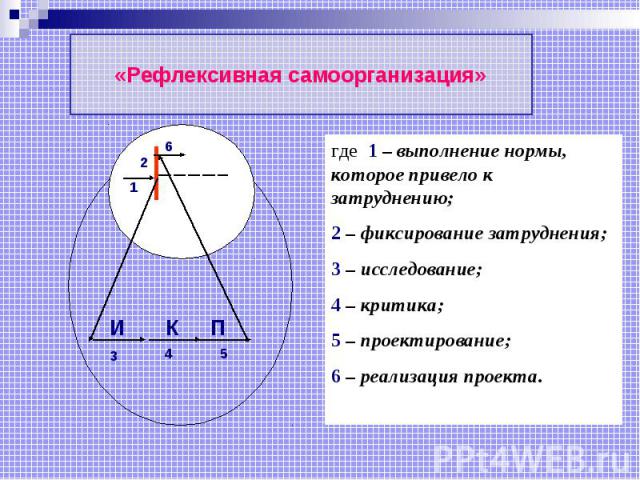
«Рефлексивная самоорганизация» где 1 – выполнение нормы, которое привело к затруднению; 2 – фиксирование затруднения; 3 – исследование; 4 – критика; 5 – проектирование; 6 – реализация проекта.

РЕШИТЕ ЗАДАЧУ: Определите, какой геометрической фигуры не хватает?

РЕШИТЕ ЗАДАЧУ: Определите, какой геометрической фигуры не хватает?

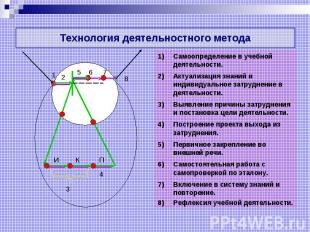
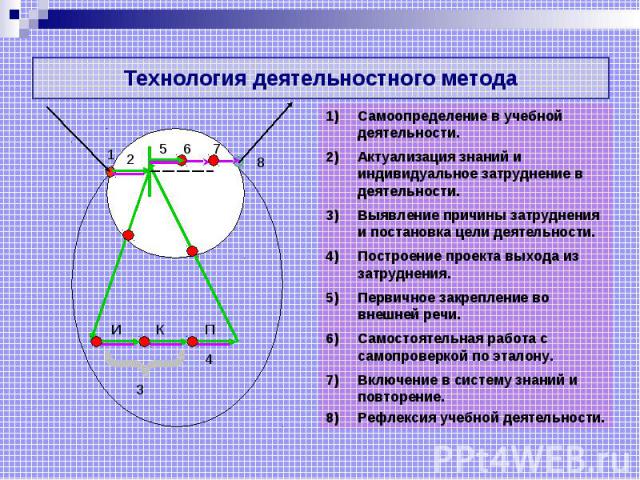
Технология деятельностного метода Самоопределение в учебной деятельности. Актуализация знаний и индивидуальное затруднение в деятельности. Выявление причины затруднения и постановка цели деятельности. Построение проекта выхода из затруднения. Первичное закрепление во внешней речи. Самостоятельная работа с самопроверкой по эталону. Включение в систему знаний и повторение. Рефлексия учебной деятельности.

О.А. Коростелева, СШ № 1743, г. МоскваТема: «Вычитание двузначных чисел с переходом через разряд» [ учебник «Математика» авт. Л.Г.Петерсон 2-й класс, ч. 1, с. 24–25] Задачи: 1) Сформировать умение вычитать двузначные числа с переходом через разряд, тренировать счетные навыки, умение самостоятельно анализировать решать составные задачи. 2) Развивать мыслительные операции, творческие и деятельностные способности , математическую речь. 3) Воспитание любви к предмету, взаимоуважения, трудолюбия аккуратности.

Ход урока:1. Мотивирование к деятельности. 2. Актуализация знаний и мотивация. 2.1. Вычитание с переходом через десяток. Учитель предлагает детям решить примеры, записанные на доске: 15 – 7 = 11 – 4 = 16 – 8 = 17 – 9 = 14 – 7 = 15 – 8 = Дети устно называют ответы, учитель записывает ответы на доске. – Что общего у всех примеров? (...) – Разбейте примеры на группы. (...) – Какие еще примеры на вычитание вы умеете решать? (...)

2.2. Вычитание двузначных чисел без перехода через разряд. На доске и на листках у каждого ребенка записано: – Что интересного в разностях? (...) – Найдите неизвестную цифру уменьшаемого, если известно, что разность между его цифрами десятков и единиц равна 3? (...) При проверке решения выставляется алгоритм вычитания двузначных чисел (общий случай) В завершение фиксируется затруднение в деятельности.

2.3 Постановка проблемы. – Какое действие мы выполняли? (...) – Чем отличается данный пример от предыдущих? (...) – Значит, чему нам надо научиться? (...) Цель урока: научиться вычитать двузначные числа, если в уменьшаемом не хватает единиц. – Как бы вы назвали этот случай вычитания? Тема урока: «Вычитание двузначных чисел с переходом через разряд»

3.Проблемное объяснение знаний ( «открытие» детьми нового знания). – Какие способы решения примеров вы знаете? – Каким способом вы предлагаете найти верный ответ? – Начнем с моделей. Дети выкладывают перед собой, а один ребенок – на демонстрационной доске модель примера: – Как вычитают двузначные числа? (...) – А почему здесь не можем вычесть? (...) – У нас что, уменьшаемое меньше? (...) – А куда же спрятались единицы? (...) – И как же нам вычесть? (!!!) – Выполните вычитание и определите, что получилось. Молодцы! • 10 Новый алгоритм фиксируется в речи и знаково: 4 1 Выставляется эталон. 2 4 1 7

4. Первичное закрепление с комментированием в громкой речи. 1) № 1, стр. 24 – Проверьте, верно ли решен первый пример? Объясните решение. – Решите следующие примеры в парах по выбору с объяснением. У кого что получилось? Дети дорисовывают графические модели и одновременно комментируют решение примеров в парах. Линией соединяют ответы с числовой записью и дописывают ответ. Те, кто закончил раньше других, комментируют вслух для всего класса, остальные дети сверяют со своим решением. 2) № 2, стр. 24 8 1 8 2 8 3 8 4 8 5 8 6 8 7 8 8 2 9 2 9 2 9 2 9 2 9 2 9 2 9 2 9 5 2 5 3 5 4 !!! 3) № 3, стр. 24. Игра «Угадай-ка». (Работа в парах.)

5. Самостоятельная работа с самопроверкой по эталону. 1) – Выберите из записанных на доске примеров и запишите в столбик те примеры, которые решаются с помощью нового вычислительного приема: 2) После проверки правильности выбора выбрать из записанных на доске примеров те, которые решаются с помощью нового вычислительного приема: 9 8 7 6 5 4 1 9 1 8 1 7 7 9 5 8 3 7 ? 3) Коррекция возможных ошибок. 4) Что интересного в примерах? Какой пример следующий? Сохранится ли закономерность?

6. Включение в систему знаний и повторение. Работа в парах: № 9 (а, б) – одна задача по выбору. Двое работают на закрытой доске. Проверка – фронтально с анализом задачи. 7. Рефлексия деятельности (итог урока) – Что нового узнали? – Каким способом? – Кого мы можем сегодня похвалить? – Как каждый из вас оценивает свою работу? Дома: 1) Придумать свой пример на новый вычислительный прием, нарисовать его графическую модель и решить. 2) По желанию: расшифровать название сказки в № 5, стр. 25

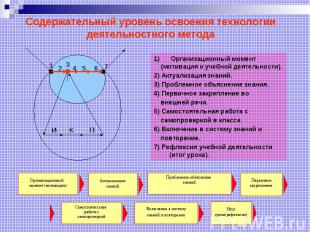
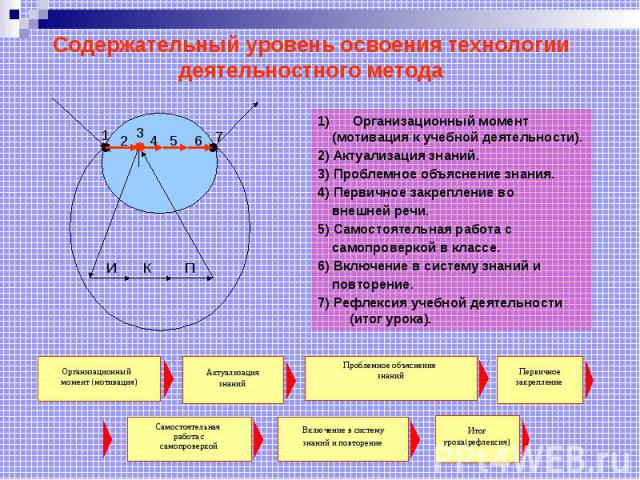
Содержательный уровень освоения технологии деятельностного метода Организационный момент (мотивация к учебной деятельности). 2) Актуализация знаний. 3) Проблемное объяснение знания. 4) Первичное закрепление во внешней речи. 5) Самостоятельная работа с самопроверкой в классе. 6) Включение в систему знаний и повторение. 7) Рефлексия учебной деятельности (итог урока).

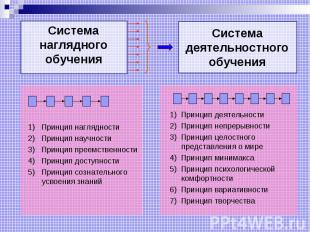
Система наглядного обучения 1) Принцип наглядности 2) Принцип научности 3) Принцип преемственности 4) Принцип доступности 5) Принцип сознательного усвоения знаний Система деятельностного обучения 1) Принцип деятельности 2) Принцип непрерывности 3) Принцип целостного представления о мире 4) Принцип минимакса 5) Принцип психологической комфортности 6) Принцип вариативности 7) Принцип творчества

Система дидактических принципов «Школа 2000...»

Он взрослых изводил вопросом «Почему?». Его прозвали «маленький философ». Но только он подрос, как начали ему Преподносить ответы без вопросов. И с этих пор он больше никому Не задавал вопроса «Почему?».

Центр системно-деятельностной педагогики «Школа 2000…» Академии ПК и ППРО РФИнтернет: www.sch2000.ru e-mail: [email protected] тел. (095) 797-89-77, 452-22-33 Адрес: 125212 Москва, Головинское шоссе, д.8, корп.2

Успехов в работе!