Презентация на тему: Интерактивная математика в образовательных учреждениях XXI века

КОНКУРС ИНТЕРАКТИВНЫХ ПЛАКАТОВ «Интерактивная математика в образовательных учреждениях XXI века» Гаврилькова Ирина Юрьевна МОУ «СОШ № 2 с углубленным изучением отдельных предметов» г. Новый Оскол Учитель математики I квалификационная категория

ПУТЕВОДИТЕЛЬ История математики приложения Великие математики и их открытия приложения Математические загадки приложения

Математика (греч. mathematike, от máthema — знание, наука), наука о количественных отношениях и пространственных формах действительного мира. Счёт предметов на самых ранних ступенях развития культуры привёл к созданию простейших понятий арифметики натуральных чисел. Только на основе разработанной системы устного счисления возникают письменные системы счисления и постепенно вырабатываются приёмы выполнения над натуральными числами четырёх арифметических действий (из которых только деление ещё долго представляло большие трудности). Потребности измерения (количества зерна, длины дороги и т.п.) приводят к появлению названий и обозначений простейших дробных чисел и к разработке приёмов выполнения арифметических действий над дробями. Таким образом накапливается материал, складывающийся постепенно в древнейшую математическую науку — арифметику. Измерение площадей и объёмов, потребности строительной техники, а несколько позднее — астрономии, вызывают развитие начатков геометрии. Эти процессы шли у многих народов в значительной мере независимо и параллельно. Особенное значение для дальнейшего развития науки имело накопление арифметических и геометрических знаний в Египте и Вавилонии. В Вавилонии на основе развитой техники арифметических вычислений появились также начатки алгебры, а в связи с запросами астрономии — начатки тригонометрии.

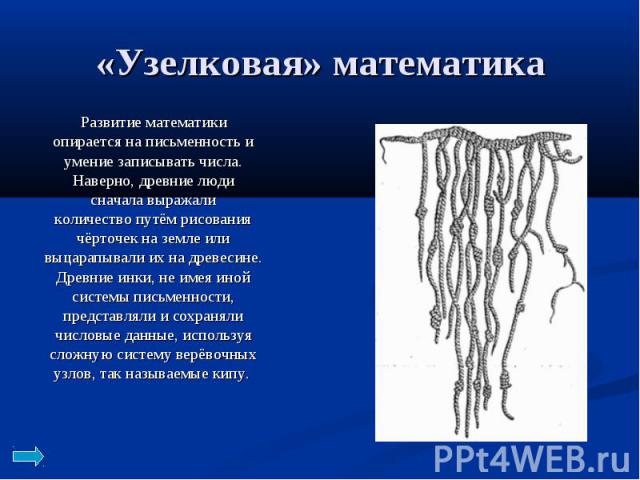
«Узелковая» математикаРазвитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу.

Математика АристотеляКо времени Аристотеля теоретическая математика прошла значительный путь и достигла высокого уровня развития. Продолжая традицию философского анализа математического познания, Аристотель поставил вопрос о необходимости упорядочивания самого знания о способах усвоения науки, о целенаправленной разработке искусства ведения познавательной деятельности, включающего два основных раздела: "образованность" и "научное знание дела". Среди известных сочинений Аристотеля нет Специально посвященных изложению методологических проблем математики. Но по отдельным высказываниям, по использованию математического материала в качестве иллюстраций общих методологических положений можно составить представление о том, каков был его идеал построения системы математических знаний.

Врата и ключ этих наук – математика, которую, как я докажу, открыли безупречные мужи от начала мира и которую предпочитали прочим наукам все безупречные и мудрые. А пренебрежение ею уже на протяжении 300 или 400 лет разрушило всякое знание у латинян. Ибо, не зная её, нельзя знать, как я покажу далее, ни прочих наук, ни мирских дел. И что ещё хуже, люди, в ней не сведущие, не ощущают собственного невежества, а потому не ищут от него лекарства. И напротив того, знакомство с этой наукой подготовляет душу и возвышает её ко всякому прочному знанию, так что, если кто познал источники мудрости, касающиеся математики, и правильно применил их к познанию прочих наук и дел, тот сможет без ошибок и без сомнений, легко и по мере сил постичь и все последующие науки. Роджер Бэкон

Пьер Ферма Пьер де Ферма — французский математик, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. В отличие от Галилея, Декарта и Ньютона, Ферма был чистым математиком — первым великим математиком новой Европы. Независимо от Декарта он создал аналитическую геометрию. Но главная его заслуга — создание теории чисел.

Михаил Васильевич Ломоносов Михаил Васильевич Ломоносов первый русский учёный естествоиспытатель мирового значения, энциклопедист, химик, математик и физик. Михаил Васильевич Ломоносов является одним из великих учёных, которого без сомнений можно поставить на одно из первых мест среди разносторонне одаренных людей в истории человечества. В 1741 году Ломоносов написал сочинение, изумившее всех своим названием: Elementa Chimiae Mathematicae (”Элементы математической химии”, на латыни).

Софья Васильевна КовалевскаяСофья Васильевна Ковалевская— русский математик и механик, с 1889 года иностранный член корреспондент Петербургской Академии наук. Первая в России и в Северной Европе женщина профессор и первая в мире женщина-профессор математики. Доказала существование аналитического (голоморфного) решения задачи Коши для систем дифференциальных уравнений с частными производными.

Лауреаты Нобелевской премии по математикеПервоначально Нобель внёс математику в список наук, за которые присуждается премия, однако позже вычеркнул её, заменив премией мира. Достоверная причина неизвестна. Чаще всего её связывают с именем шведского математика, лидера шведской математики того времени Миттаг-Леффлера, которого Нобель не любил за то, что тот назойливо выпрашивал пожертвования на Стокгольмский Университет. По другой версии, Нобель был влюблён в Софью Ковалевскую, которая предпочла ему того же Миттаг-Леффлера. Ещё одна версия: у Нобеля была возлюбленная, Анна Дезри, которая потом влюбилась в Франца Лемаржа и вышла за него замуж. Франц был сыном дипломата и в то время собирался стать математиком.

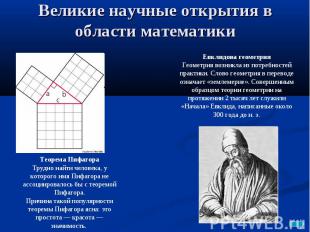
Великие научные открытия в области математикиЕвклидова геометрия Геометрия возникла из потребностей практики. Слово геометрия в переводе означает «землемерие». Совершенным образцом теории геометрии на протяжении 2 тысяч лет служили «Начала» Евклида, написанные около 300 года до н. э. Теорема Пифагора Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Причина такой популярности теоремы Пифагора ясна: это простота — красота — значимость.

Логарифмы На всем протяжении XVI века основную трудность в математике, представляли умножение и деление многозначных чисел, особенно тригонометрических величин. Ясность внесли таблицы логарифмов Джона Непера. Основы алгебры. Франсуа Виет Первым обозначать буквами не только неизвестные, но и данные величины стал Франсуа Виет. Ему удалось внедрить в науку мысль о возможности выполнять алгебраические преобразования над символами, т. е. ввести понятие математической формулы. Великая теорема Ферма связана не только с алгебраической теорией чисел, но и с алгебраической геометрией, которая сейчас интенсивно развивается. Пьер Ферма стал основателнм математической теории вероятностей.

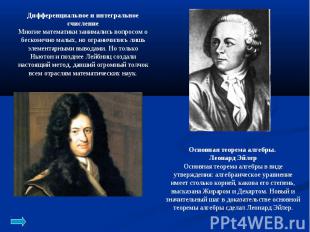
Дифференциальное и интегральное счисление Многие математики занимались вопросом о бесконечно малых, но ограничились лишь элементарными выводами. Но только Ньютон и позднее Лейбниц создали настоящий метод, давший огромный толчок всем отраслям математических наук. Основная теорема алгебры. Леонард Эйлер Основная теорема алгебры в виде утверждения: алгебраическое уравнение имеет столько корней, какова его степень, высказана Жираром и Декартом. Новый и значительный шаг в доказательстве основной теоремы алгебры сделал Леонард Эйлер.

"Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным".               Б. Паскаль

Математические загадки и ребусы Прах Диофанта Прах Диофанта гробница покоит; Дивись ей — и камень Мудрым искусством его Скажет усопшего век. Волей богов шестую часть жизни он прожил ребенком И половину шестой встретил с пушком на щеках. Только минула седьмая, с подругою он обручился, С нею, пять лет проведя, сына дождался мудрец. Только полжизни отцовской возлюбленный сын его прожил, Отнят он был у отца ранней могилой своей. Дважды два года родители оплакивали тяжкое горе. Тут и увидел мудрец предел жизни печальной своей. (64 года)

Любитель порядка Настольная лампа, Зеленый диван, Сидит на диване Матюшин Иван. Он пишет... Не будем, ребята, мешать, А только тихонько Заглянем в тетрадь. В тетрадке написано Все по порядку: «В семь двадцать встаем, Производим зарядку. В восемь тридцать, Умывшись холодной водой, Застелем постель И займемся едой. Без четверти восемь Дрова мы приносим. Готовим по плану Похлебку Полкану — И в класс направляемся В восемь ноль пять». Вопрос: сколько времени уходит у Ивана от подъема до выхода в школу? (45 мин)

Жуки и пауки Вопрос: сколько ног у жука? Сколько ног у паука? У меня в одной коробке три жука, А в другой имею я три паука. В уголке шуршат бумагой два ежа, А в двух клетках распевают два чижа. Кто, ребята, сосчитать бы мне помог, Сколько вместе все они имеют ног? (54 ноги)

подобие теорема наклонная отрезок указатель

При подготовке презентации использованы материалы: Ван-дер-Варден Б.Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. М., 1959 Юшкевич А.П. История математики в средние века. М., 1961 Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики. М., 1986 Клейн Ф. Лекции о развитии математики в XIX столетии. М., 1989

Источники иллюстраций:http://images.yandex.ru/