Презентация на тему: Знакомьтесь, уравнение

Карл Фридрих Гаусс (1777-1855) немецкий математик, астроном, геодезист и физик, иностранный член-корреспондент (1802) и иностранный почетный член (1824) Петербургской АН О, математика. В веках овеяна ты славой,Светило всех земных светил. Тебя царицей величавойНедаром Гаусс окрестил. Строга, логична, величава,Стройна в полёте, как стрела,Твоя немеркнущая славаВ веках бессмертье обрела. Мы славим разум человека, Дела его волшебных рук, Надежду нынешнего века, Царицу всех земных наук. Поведать мы сегодня вам хотимИсторию возникновения того, Что каждый школьник должен знать –Историю квадратных уравнений, А также их уметь решать.

Знакомьтесь, уравнение! Работу выполнила ученица 9-го класса Лёвина Дарья

Определение квадратного уравнения Уравнение вида где х – переменная, а, b и c – некоторые числа, причем а 0 называется квадратным уравнением

Выражение называется дискриминантом
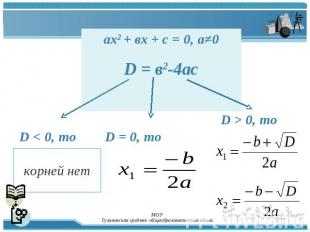
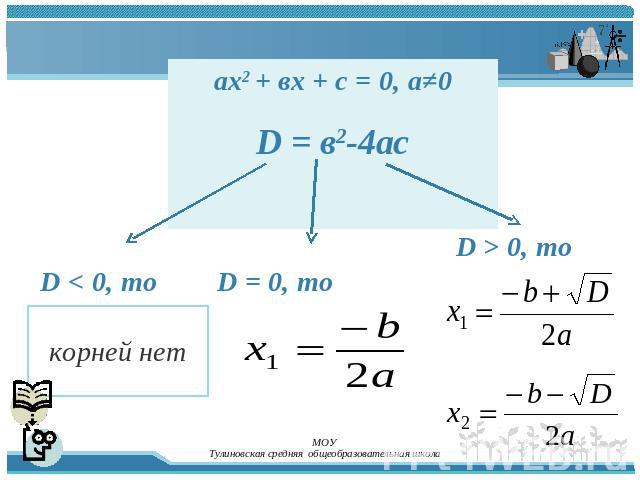
aх2 + вх + с = 0, а≠0D = в2-4ас D < 0, то D = 0, то D > 0, то корней нет

Исторические сведения Необходимость решать уравнения не только первой, но и второй степени в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и работами военного характера, с развитием астрономии и математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.

Цель исследования: Выяснить, можно ли решать квадратное уравнение с помощью циркуля и линейки

Гипотеза По данным действительным коэффициентам a, b, c уравнения ax2 + bx + c = 0 (a ≠ 0) можно определить радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения

Ход исследования: 1. Изучив теоретический материал учебника и дополнительных источников информации выяснить, способы решения квадратных уравнений с помощью циркуля и линейки.2. Изучить историю квадратных уравнений.3. Оформить результаты, сделать соответствующие выводы.

Задача. По данным действительным коэффициентам a, b, c уравнения ax2 + bx + c = 0 (a ≠ 0) определить радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения .
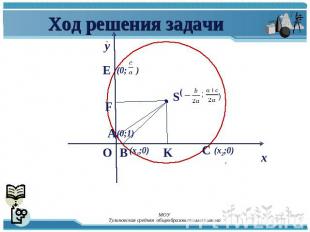
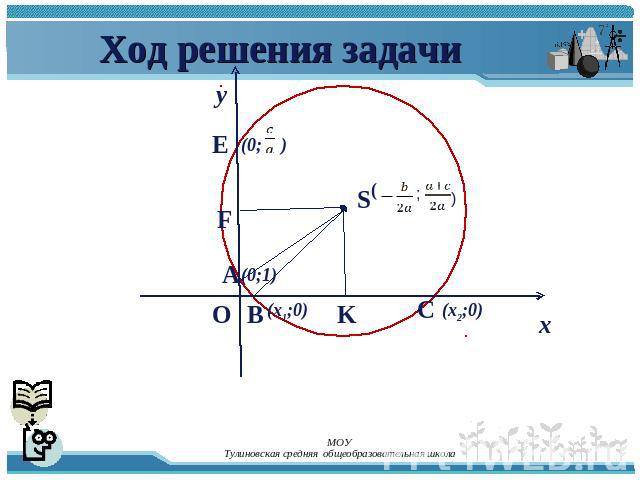
Ход решения задачи

План нахождения корней квадратного уравнения с помощью циркуля и линейки В системе координат построим точки и А (0;1).Проведём окружность с радиусом SA.3. Абсциссы точек пересечения окружности с осью Ох являются корнями исходного квадратного уравнения.
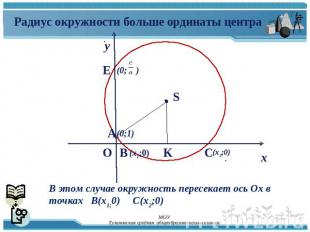
Радиус окружности больше ординаты центра В этом случае окружность пересекает ось Ох в точках В(х1;0) С(х2;0)
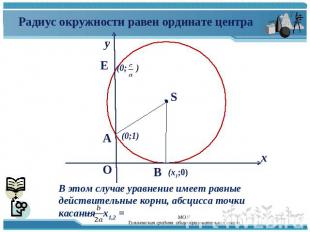
Радиус окружности равен ординате центра В этом случае уравнение имеет равные действительные корни, абсцисса точки касания х1,2 =
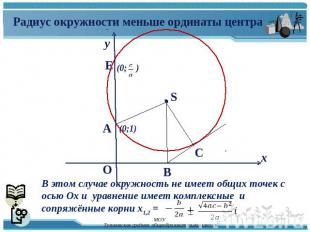
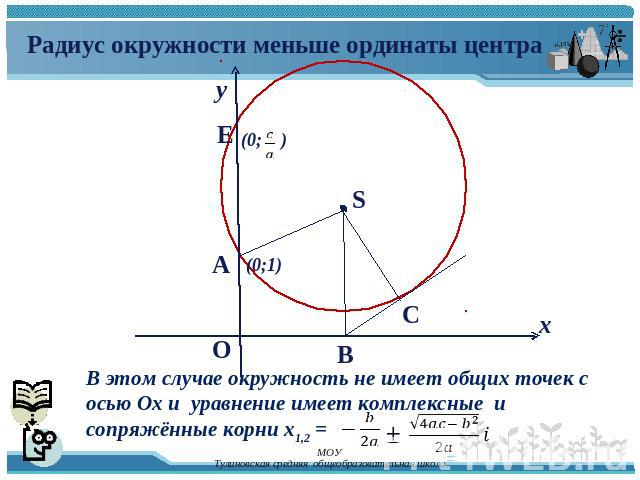
Радиус окружности меньше ординаты центра В этом случае окружность не имеет общих точек с осью Ох и уравнение имеет комплексные и сопряжённые корни х1,2 = =

Примеры: а) 2x2 + 3x + 1 = 0 Определим координаты точки центра окружности по формулам: Проведём окружность радиуса SA, где А(0;1). Корни уравнения -1 и - 0,5.

Примеры: б) x2 - 5x + 6 = 0 Определим координаты точки центра окружности по формулам: Проведём окружность радиуса SA, где А(0;1). Корни уравнения 2 и 3.

1. Квадратные уравнения можно решать с помощью циркуля и линейки.2. По данным действительным коэффициентам a, b, c уравнения ax2 + bx + c = 0 (a ≠ 0) можно определить радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения

Способы решения квадратных уравнений Изучаемые в школе: Разложение левой части на множители Метод выделения полного квадрата С применением формул корней квадратного уравнения С применением теоремы Виета Графический способ

Способы решения квадратных уравнений Продвинутые способы: Способ переброски По свойству коэффициентов С помощью циркуля и линейки С помощью номограммы Геометрический

Глейзер Г.И. История математики в школе. – М., Просвещение, 1982. Лиман М.М. Школьникам о математике и математиках. - М., Просвещение, 1981. Пичугин Л.Ф. За страницами учебника алгебры. – М., Просвещение, 1990.Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. – М., квант, № 4/72, стр.34.Ткачёва М.В. Домашняя математика. –М., Просвещение, 1994.Энциклопедический словарь юного математика. – М., Педагогика, 1985.