Презентация на тему: Вся правда о золотом сечении

Вся правда о золотом сечении РАБОТА ПОДГОТОВЛЕНА ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ УЧЕНИКОВ, УВАЖАЮЩИХ МАТЕМАТИКУ

Работу представляет Работу представляет Климова Елизавета, ученица 7 «В» класса лицея № 44 г. Липецка1 декабря 2008 г.

Золотым сечением издавна называют число – определенное соотношение длин отрезков. Золотое отношение обычно обозначают буквой – прописной буквой греческого алфавита. Такое обозначение принято в честь древнегреческого скульптора Фидия, жившего в V в. до н.э. Он руководил строительством храма Парфенон в Афинах в пропорциях этого храма многократно присутствует число . Считается, что понятие золотого сечения ввел Пифагор, атермин «золотое сечение» придумал Леонардо да Винчи он назвал так деление отрезка в отношении .

Пифагор Самосский (VI в. до н. э.) Леонардо да Винчи (1452 - 1519) Выясним, чему же равно число .

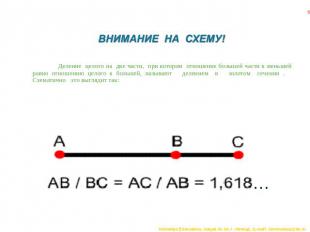
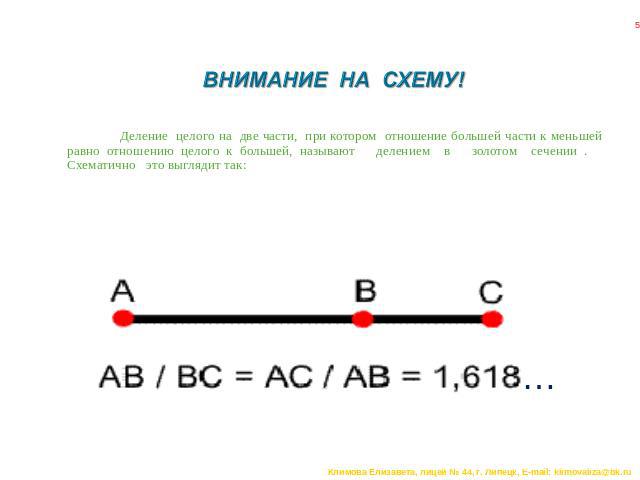
ВНИМАНИЕ НА СХЕМУ! Деление целого на две части, при котором отношение большей части к меньшей равно отношению целого к большей, называют делением в золотом сечении . Схематично это выглядит так:

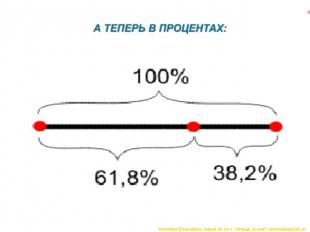
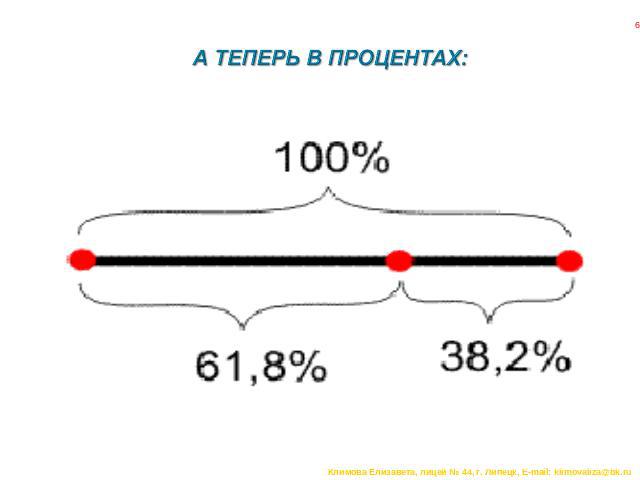
А ТЕПЕРЬ В ПРОЦЕНТАХ:

 Какова величина отношения ширины каждого витка спирали к предыдущему у любой улитки? Какова величина отношения ширин колец Сатурна?  При расчетах получается одно и тоже число, приблизительно равное 1,6 или, если быть точнее 1.61803398874989... Случайно ли это?   

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью , а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление совершенства соотношения целого и его частей в искусстве, науке, технике и природе.

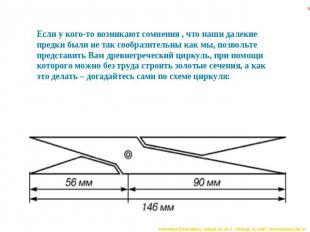
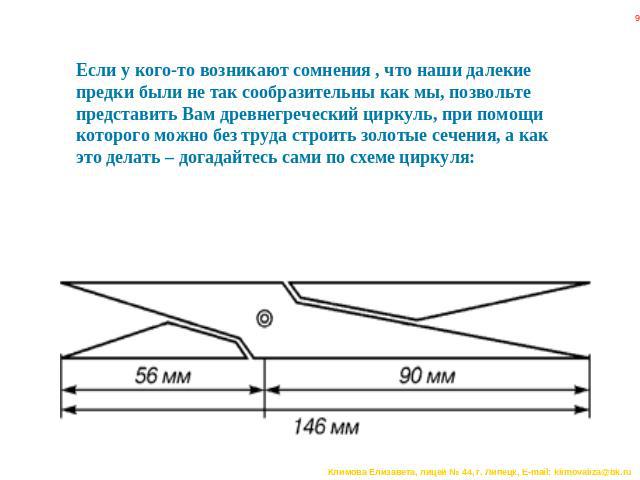
Если у кого-то возникают сомнения , что наши далекие предки были не так сообразительны как мы, позвольте представить Вам древнегреческий циркуль, при помощи которого можно без труда строить золотые сечения, а как это делать – догадайтесь сами по схеме циркуля:

А как обстоят дела у живых существ? У многих бабочек узоры на крыльях, соотношение размеров грудной и брюшной части тела соответствуют золотой пропорции.

Как-то раз себе на гореЗаплыла с линейкой в море,Долго в воду я нырялаИ дельфинов измеряла.

Может каждый мне поверить – Эту морду страшно мерить !

Пентаграмма Пентаграмма – тайный знак пифагорейского братства – была выбрана в качестве символа жизни и здоровья.Что же это?

Золотой пятиугольник (пентаграмма) Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый, создал это построение великий Евклид при помощи циркуля. И в наши дни пентаграмма красуется на флагах и гербах многих стран. Что же привлекает к ней внимание людей? Дело в том, что в ней многократно повторяется одно и то же отношение состав-ляющих ее отрезков. И это отношение – золотое сечение. Например: AD/AC = AC/CD = AB/BC = Φ

Американский доктор пластической хирургии Stephen Marquardt вывел формулу идеального лица, в основе которой лежит пентаграмма. Изобретение было запатентовано и широко используется в пластической хирургии.

Золотое сечение в пропорциях лица Маска идеального лица доктора Stephena MarquardtaРазные культуры, разное время…

Плитки Пенроуза В античной науке была широко известна «проблема паркета», которая сводится к плотному заполнению плоскости геометрическими фигурами одного вида. Как известно, такое заполнение может быть осуществлено с помощью треугольников, квадратов и шестиугольников. С помощью пятиугольников (пентагонов) такое заполнение невозможно.

Рассмотрим еще раз внимательно правильный пятиугольник: Как известно, после проведения в пентагоне диагоналей исходный пентагон может быть представлен как совокупность трех типов геометрических фигур. В центре находится новый пентагон, образуемый точками пересечения диагоналей. Остальная часть пентагона включает в себя пять равнобедренных треугольников, окрашенных в желтый цвет, и пять равнобедренных треугольников, окрашенных в красный цвет. Желтые треугольники являются «золотыми», так как отношение бедра к основанию равно золотой пропорции; они имеют острые углы в 36° при вершине и острые углы в 72° при основании. Красные треугольники также являются «золотыми», так как отношение бедра к основанию равно золотой пропорции; они имеют тупой угол в 108° при вершине острые углы в 36° при основании. А теперь соединим два желтых треугольника и два красных треугольника их основаниями. В результате мы получим два «золотых» ромба. Пер-вый из них (желтый) имеет острый угол в 36° и тупой угол в 144°. Левый ромб будем называть тонким ромбом, а правый ромб – толстым ромбом.

Английский математик и физик Роджерс Пенроуз использовал «золотые» ромбы для констру-ирования «золотого» паркета, который был назван плитками Пенроуза. Плитки Пенроуза представляютсобой комбинацию толстых итонких ромбов. Важно подчеркнуть, чтоотношение числа толстых ромбов к тонким стремится к золотой пропорции!

Лечение пирамидой Золотые пропорции помогают не только укладывать паркет, но и лечить людей. Лечебными свойствами обладает практически любая пирамида, похожая пропорциями на египетские. С помощью пирамид можно нормализовать сон и давление, восстановить многие функции организма. Переломы срастаются быстрее, послеоперационные швы – тоже. Лечение пирамидами может производиться следующими методами: Поместить больного под большую пирамиду. Поместить больной орган (рука, нога) под пирамиду. Зарядить в течение суток или более, под пирамидой алюминиевую фольгу и прибинтовать к больному месту на несколько часов. Поместить под кровать больного 1-4 пирамидки. Посадить больного на стул со спинкой, а под стул поставить пирамидку. Зарядить воду в закрытой бутылке под пирамидой (1 –14 дней). Вода должна заряжаться в нижней трети пирамиды (условно мертвая вода) и отдельно выше нижней трети пирамиды (условно живая вода). При зарядке вода не должна составлять более 10% от объёма пирамиды.

Мясо в пирамиде не тухнет, вода при -30 градусах не замерзает,а затупленные лезвия вновь становятся острыми. Домашняя пирамида может иметь любые размеры, но соотношение ее высоты и длины основания должно быть строго определенным, а именно:длина основания должна превышать высоту пирамиды в 1,6 раза. Такое соотношение соответствует пропорции золотого сечения. С удвоением высоты пирамиды активность ее действия возрастаетво много (50-100 и более) раз. Следовательно, устанавливайтепирамиды с максимальной высотой. Одно из ребер пирамиды должно быть сориентировано с помощью компаса строго на север.На высоте 1/3 , 1 / 2 и 2/3 пирамиды устанавливаются полочки.

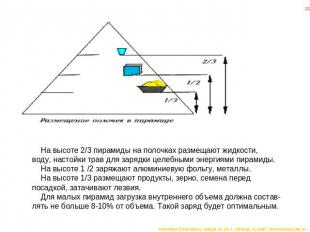
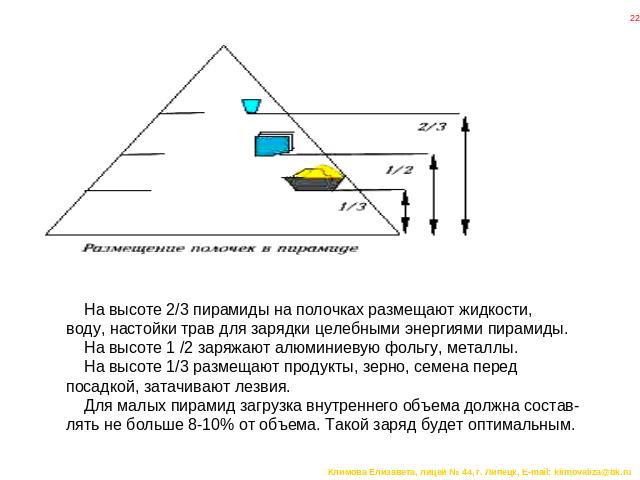
На высоте 2/3 пирамиды на полочках размещают жидкости, воду, настойки трав для зарядки целебными энергиями пирамиды. На высоте 1 /2 заряжают алюминиевую фольгу, металлы. На высоте 1/3 размещают продукты, зерно, семена перед посадкой, затачивают лезвия. Для малых пирамид загрузка внутреннего объема должна состав-лять не больше 8-10% от объема. Такой заряд будет оптимальным.

Можно ли измерить красоту нашего мира? На этот вопрос сложно ответить. Однако точно можно утверждать, что какая-то неведомая нам сила создаёт всё прекрасное и гармоничное согласно законам золотого сечения. Трудно оторвать глаза от красоты, она так притягательна, может причина в нем – золотом и божественном. Надо заметить, человек способен интуитивно чувствовать пропорции сечения. Работая над картиной, вышивкой или костюмом, сам того не зная, человек закладывает его в свои творения. Ничего удивительного, ведь золотая пропорция у нас всегда перед глазами, в виде самих себя.